X-ٌَRAYS to identify an unknown substance
Discovered in 1895 by the German physicist Röntgen, X-rays are at the basis of various analytical techniques such as radiography, spectroscopy and diffractometry. These electromagnetic radiations have a wavelength of the order of Ångström (1 Å = 10-10 m).
A crystal is an arrangement of atoms, ions, or molecules, with a pattern repeating itself periodically in all three dimensions. The interatomic distances are of the order of Ångström, of the same order of magnitude as the wavelengths of the X-rays: a crystal thus constitutes a 3D network which can diffract X-rays.
In 1913, William Lawrence Bragg and his father Sir William Henri Bragg used this radiation to determine the crystal structure of NaCl and many other metal salts. They were jointly awarded the Nobel Prize for Physics in 1915 for their contributions to "the analysis of the crystal structure by means of X-rays".
We present the basic theory of the interaction of X-rays with solid structures as well as the implementation of examples of applications: crystal structure resolution on single crystals and phase recognition in crystallized solids.
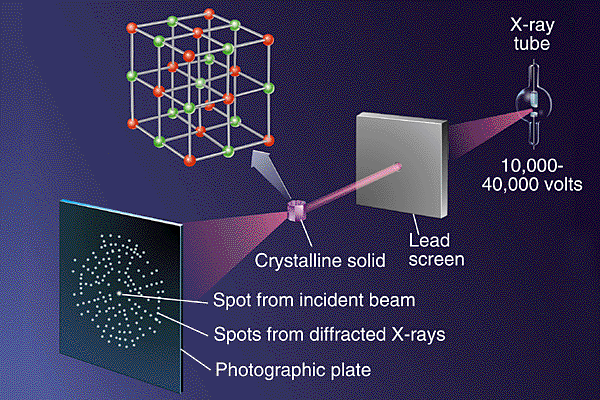

Principle of the experiment:


We consider, in a crystal mesh:
A plane formed of a set of atoms.
Family of atomic planes.
An incident beam consisting of X-ray of wavelength λ is diffracted by this family of atomic planes.
We will have a diffraction peak if its angle of incidence θ on the planes satisfies the Bragg relation: 2d. Sin θ = nλ (n = 1).
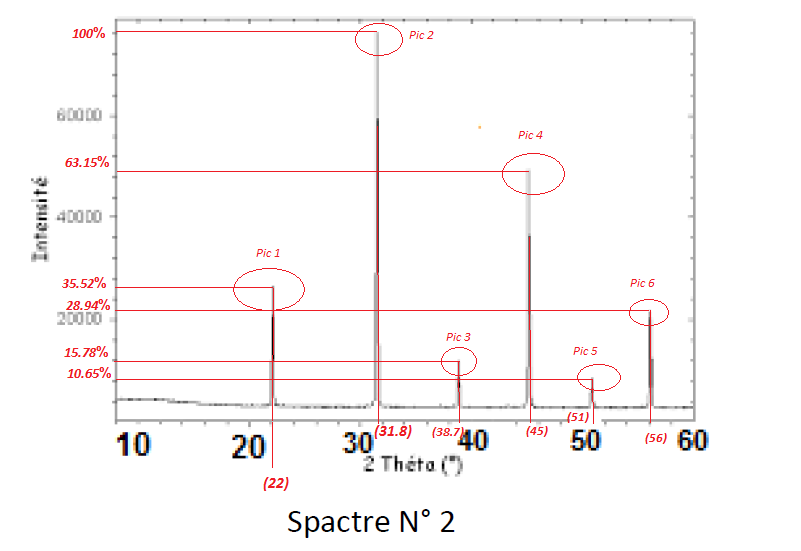
Using Bragg's law, calculates inter-reticular distances dhkl on the N 2 spectrum.
dhkl = λ / 2.Sin θ
• d: inter-reticular distance, that is to say distance between two crystallographic planes.
• θ: half-deflection angle (half of the angle between the incident beam and the direction of the detector).
• λ: X-ray wavelength. (Λ = 1.5406Ao) = 1).
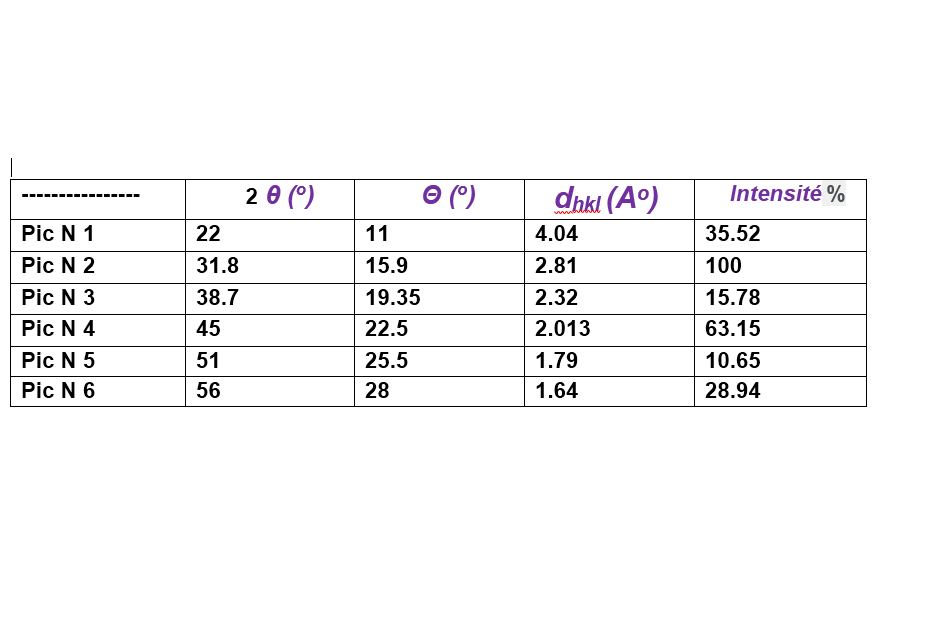
Ranking of the dhkl results:
4.04 (Ao)> 2.81 (Ao)> 2.32 (Ao)> 2013 (Ao)> 1.79 (Ao)> 1.64 (Ao)
It has been found that when the value of the diffraction angle θ increases, the value of the inter-reticular distance dhk1 decreases.
By comparing the following results: 4.04 / 2.81 / 2.32 (the first three results) with the results of the dhkl that we have already calculated.
From the N2 spectrum and comparisons of the calculated values of dhkl (the first three) with the values of the database found that the analyzed substance is that of SeO2.
Conclusion:
From the diffracted intensities and the inverse relation (real network-reciprocal lattice), it is possible, from a series of diffraction images on a single crystal, to determine the three-dimensional arrangement of the atoms of a crystalline structure. . This method has become very important in recent years.
At the end, accept, Madam, Sir, my respectful (or "sincere") greetings.
Thank you @benainouna! It is a very intriguing technique and it has become very important especially with the rise of X-ray crystallography for proteins. I checked out your blog and followed you. I write similar content and maybe you can find some interesting articles on my blog. I appreciate another science writer on here! Cheers @lesshorrible!
i will :),and i wish we learn as much as we can from each other :) Thank you
Awesome! Just a tip right of the bat: include your sources( for example for your pictures). I would recommend checking out some of the already successful science writers like @lemouth, @thescientist or @mcw and see what they do to write compelling stories. Looking forward to read more!
that's nice from you, i will work with your advices thank you so much
Your next post could be about XRF (X-ray Fluorescence), not related, but still - X-rays
thank you for finding time for reading this post :) ,well i did'nt work with this method before i like to know more about it