[수학] 나무막대기와 삼각형

아침엔 약간 어두컴컴(?)했는데

점심 때가 되서 산꼭대기(?)에 오르니 해가 있네?

그리고 아직 눈이 다 안녹았네?

ㅋㅋㅋㅋ

산을 타고 내려오면서

여러 이야기를 하다가

오랜만에 등산에 힘에 겨워 기다란 나무막대기를 지팡이 삼아 내려오는데

문득 유명한 수학 문제 하나가 떠올랐다.

나무 막대기를 아무렇게나 세 조각으로 잘랐을 때, 그 조각들이 삼각형을 만들 수 있는 확률을 얼마나 될까

ㅋㅋㅋㅋㅋㅋ

엊그제 트라이앵글, ㅋㅋㅋ삼각형 관련 영화를 봐서 ㅋㅋㅋㅋ

퀴즈도 삼각형 관련 문제를 냈고 ㅋㅋㅋㅋ
최소거리랑 페르마의 점 관련 포스팅 도 쓰고 ㅋㅋㅋㅋ

---

그래 오늘 포스팅 거리는 이걸로 하자

---

편의상 막대기의 길이를 1m 라 하자

삼각형은 세 변(a,b,c 라 하자) 으로 이루어져있는데

임의의 세 선분 가지고 삼각형을 만들 수 없다.

중학교 때, 우리는 삼각형의 성립 조건을 배웠다.

가장 긴 변의 길이는 나머지 두 변의 길이의 합보다 작다.

가장 긴 변의 길이를 c 라 한다면

c<a+b

즉 가장 긴 변이 c가 0.5m 이상이라면 (50cm) 저 부등호를 만족시킬수 없기에

최소한 a,b,c, 모두 0.5보다 작다는 것을 알 수 있다.

자 이제 문제를 다르게 생각해보자.

막대의 어느 부분을 잘라야 a,b,c 모두 0.5 보다 작게 자를 수 있을까?

막대를 세 조각을 내기 위해선 두번 잘라야 하는데

a,b,c 모두 0.5m 보다 작게 자르려면 일단은 첫번째 자르는 지점은 앞 부분에 두번째 자르는 부분은 뒷부분에 자르되 그 사이가 0.5 보다 작아야 된다

자 일단 이렇게 되려면 첫번째로 자르는 지점과 두번째로 자르는 지점이 무게 중심을 두고 서로 앞 뒤에 있어야 한다.

이렇게 될 확률은 1/2 이다. [엄밀하게 하려면 적분을 통해 보일수 있겟으나 가운데를 중심으로 두고 서로 맞은편에 있을 확률은 막대를 중심을 기준으로 반으로 접어서 같은 구역에 있을 확률과 같기에 1/2 이 된다는 것을 생각 할 수 있다. ]

자 그럼 이제 두 지점 사이의 거리가 0.5 보다 작거나 0.5 보다 크거나 할 확률을 구하면 되는데 대칭을 생각해보면 0.5 보다 크거나 작거나 할 확률이 같다는 것을 알 수 있다. [1/2]

이 사건은 동시에 일어나는 사건이기에 1/2 x 1/2 = 1/4

25프로의 확률로 삼각형을 만들 수 있다! [생각보다 수치가 낮은데? ㅋㅋㅋ]

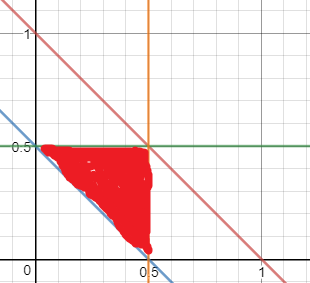
사실 이렇게 푸는 것 보다 그래프를 이용해서 풀면 좀 더 쉽다.

x,y, 1-x-y- 이렇게 세 조각을 나누어서

삼각형의 세 변의 길이는 양수이기에

자 여기에 삼각형 성립 조건을 적용하면

자 이를 만족하게 그래프를 그려보면

저 빨간 영역의 넓이를 구하면 되는데 ㅋㅋㅋ 딱 봐도 1/4 이 아닌가! [아 엄밀하게는 빨간 영역의 넓이/ 전체 넓이 ]

길이를 변수로 두고 적분으로 구하는 풀이는 Stick Broken Into Three Pieces 를 보면 될듯.. [전반적으로 여러가지 풀이에 대한 참고문헌은 A rod is broken into three parts- what is the probability that the three parts can be arranged to form a triangle?를 참조하면 될듯 내가 푼 방식도 다 나오와있다. ]

개인적으로 이 그래프를 이용한 풀이가 가장 마음에 들어서

대게 교과서에는 맨 처음 풀이와 적분을 이용한 풀이를 다루는데

시각적으로 변수를 도입하여 그래프로 보는게 가장 편한듯!