[수학, 계산] Raychaudhuri equation in time-like geodesic
오늘은 블랙홀의 singularity theorem 을 공부하다 보면 만나게 되는 Raychaudhuri equation 의 유도 방법에 대해서 소개해 볼까 합니다.
[Documentary on Amal Kumar Raychaudhuri, the renowned theoretical physicist from Kolkata]
학계에서도그닥 잘 알려지지 않은 사람입니다. [Singularity theory 나 cosmology 를 공부하는 소수에게만 알려져 있죠..] 인도 태생의 물리학자로 이름을 딴 방벙식이 있습니다만, 저도 이 방정식 하나만 들어봤지 이 사람의 삶 자체에 대해서는 거의 알지 못했습니다. 사실 이 사람의 방정식을 이용한 방법 말고 다른 방법으로 singularity theorem 을 증명하는게 있는데 그게 더 대중적(?) 이지 않나 싶네요. 그래도 이분의 이름이 들으간 방정식을 다루는데 조금이라도 이 사람에 대해서 소개하기 위해 위 다큐멘터리 영상을 첨부합니다. 위의 다큐멘터리 영상을 보니 물리학자이자 훌륭한 선생님이었다고 하네요.
일반적으로 geodesic 을 timelike(space-like 은 time-like 와 똑같은 방법으로 구함) 와 null 으로 나누어서 기술하기 때문에 이 방정식도 크게 두 버전이 있습니다. 원래 original 방법은 time-like geodesic 에서 구했고 이를 sachs 가 null version 에도 확장 시킵니다.
먼저 timelike 버전을 먼저 다루어 볼까 합니다. [Spacelike 과정은 완전히 이 방법과 같습니다. space like vector 의 제곱이 1이라는 것과 metric g 의 decomposition 에서 h- uu 가 된다는 점만 고려하면 나머지 계산이 이 방법과 똑같고 같은 결과를 줍니다. ] 일반적인 textbook 과 리뷰 논문들에 나온 방법을 따라가 봅시다.
유체역학을 공부하다 보면, 벡터 장의 흐름에 의해 expansion, shear, rotation 의 효과에 대해 접하게 됩니다. 이 방정식 역시 어떤 matter 가 주는 벡터 장에서 각각 저런 효과들을 분류하고 거기서부터 dynamics 를 보는 식입니다.
이 식의 유용성은 strong 혹은 weak energy condition 에서의 singularity를 보는데 있습니다. Penrose, Hawking and Georch 의 Singularity theorem 을 증명하는데 이 방정식은 핵심 역할을 합니다.
Convention and notation
인덱스를 올리고 내리는데 mostly + metric 을 사용 (-,+,+,+) 하였고 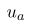 는 time-like unit vector field 를 나타냅니다. 즉
는 time-like unit vector field 를 나타냅니다. 즉  를 만족하지요. (-1 인 이유는 시간에 해당하는 metric 성분이 -1 이기 때문입니다. spacelike 의 경우 +1 이 됩니다.)
를 만족하지요. (-1 인 이유는 시간에 해당하는 metric 성분이 -1 이기 때문입니다. spacelike 의 경우 +1 이 됩니다.)
Decomposition of vector
먼저 다음과 같은 식의 분해로 부터 시작합니다. 식 전개 과정 중에 notation 을 넣어 두었기에 따로 설명 하지는 않겠습니다. 다만 강의 스타일의 전개 방식을 취할까 합니다. 즉 중간 중간 상황적 설명들을 통해 원하는 식의 형태를 만들어 나가는 과정을 보일까 합니다.
무엇을 하려고 같은 식을 여러번 적었냐면 B_{ab} 란 물리량을 traceless symmetric part 와 anti-symmetric [참고로 anti-symmetric 하면 traceless 합니다] 그리고 trace part 로 쪼개는 분해를 하려고 합니다. 리만기하학에서 리만텐서를 비슷한 방법으로 Weyl tensor, Ricci tensor 를 이용하여 분해 하곤 합니다.
일단 symmetric 과 anti-symmetric 부분으로 나누긴 했는데 symmetric 부분이 trace-less 가 되는지 알아볼 필요가 있습니다. u_{a;a} 란 값이 꼭 0 이 된다는 보장이 없기 떄문에 이 항을 빼주는 작업을 해줘야 합니다.
여기서 4차원 metric g 에서 u 부분을 합쳐 3차원 metric 을 도입하여 각 부분들이 u^a 와 수직하도록 만들 수가 있습니다.
약간의 계산을 통해 [그냥 u^a 를 곱해서 전개해보면 됩니다]
즉 h_{ab} 가 u^a 랑 수직한 3차원 metric 이라는 것을 알 수 있습니다. 이 h를 도입하면
좀 더 부연 설명을 해보자면 이 sigma 항은 symmetric traceless 하고 u^a 에 수직한 부분으로 물리적으로 shear 에 연관됩니다. w 항은 anti-symmetric 하고 u^a 에 수직한 부분으로 rotation 역할을 하고 마지막 theta 텀은 expansion 혹은 contraction 을 설명하는 항입니다.
한번 orthogonal 한지 확인해 볼까요. h가 u랑 수직하니까 사실상 sigma 가 수직한지만 확인해 보면 됩니다.

참고로 계산 도중에
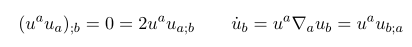
이런 관계식이 쓰였습니다. 두번째 항은 사실 geodesic 조건을 주지 않고 (그 근방의 flow 라고 했을 때) 위에 분해처럼 계산을 하게 되면 sigma와 w 항을 변형해야 합니다. 이 텀을 acceleration term 이라고 하는데 계산상의 편의를 위해 geodesic [original paper 와 대부분의 책에서 다루는] 조건을 가했습니다.
Curvature
자 이제 이 timelike vector u에 대한 curvature 정의로 부터

즉 B^{ab} B_{ab} 텀이 보이고 u^a 와 h_{ab} 의 수직 성질과 symmetric 과 anti-symmetric 의 성질 S_{ij} A^{ij} =0 으로부터
여기까지 계산 중에서 geodesic 조건을 제외하고 아무런 제약 조건을 주지 않았습니다. 여기서 아인슈타인의 장 방정식 결과를 도입하고 (on-shell 이라는 의미) 물질이 perfect fluid 라 가정하면
이 결과를 대입하면
원하고자 하는 식을 유도할 수 있습니다.
이 미분방정식은 1차 미분방정식으로 적절한 초기값을 주면 풀 수 있습니다. 이 초기값과 관련하여 우주론 연구에 적용 되기도 합니다.
Null 에서는 앞의 계수가 1/3 -> 1/2 로 바뀌게 됩니다. 다음 포스팅에서 소개해 보도록 하죠~




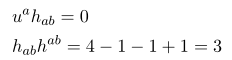

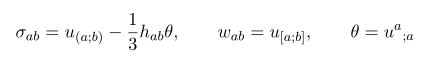
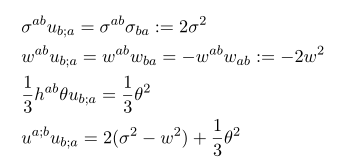

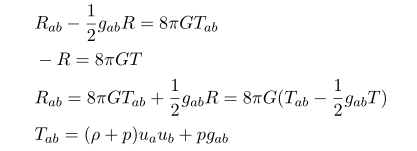
Nice
복잡한 계산이네요. 대단하네요 ㅋㅋ
이미지 파일로 수식 올리느라 고생했어요 latex 지원을 기다려봅시다 ㅋㅋ
미방 오랫만에 들어보네요 기억이 가물가물하네요
perfect fluid는 어떤 상태의 유체를 의미하는지요?
perfect fluid 는 이상적인 유체 모델로, 뒤틀림, 점성 그리고 열적 전도를 고려하지 않는 유체를 말합니다. 이는 예전글 마지막 부분에 조금 부연 설명 슬라이드를 넣어 두었었습니다 ~~ ㅎㅎ
감사합니다. 포스팅 다시 보고 오겠습니다ㅋㅋㅋ
이런 친절한 유도 과정을 보여주시다니! 감탄하고 갑니다 ㅎㅎ