Physical essentials in the Circular Uniform Movement
A uniform circular movement. When a physical object, either matter or body, performs a uniform circular motion, it describes a circumference of a given radius with constant speed, which means within this circumference, under constant speed it makes possible, that in a certain interval they are presents equal arcs.
The tangential or linear velocity is that obtained at any instant of circular motion. Determined with vectors, these will depend when it is not constant, since speed makes it possible to change direction and direction.
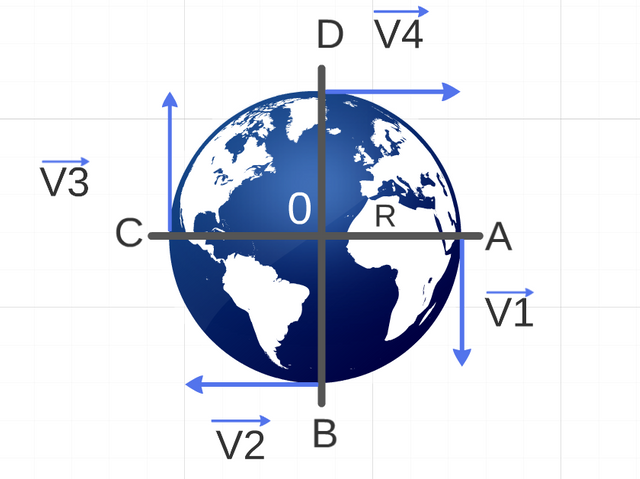
Figure - 1 (Prepared for@coolxxx.)
In this image we observe, since it is the circular uniform movement, the speed is tangential changing continuously directions and senses, with a constant speed. The speed has been represented by means of vectors in puntos:A, B, C, D.
¿How does the rapidity decide?
V = d/t.
Where d: it is a described arch, in a finished return, it would be then the length of the circumference, we have left in 2πR, multiplied by the number of times back finished "n", in an interval of time "t".
The rapidity or we have speed module left:

It expresses itself in measurement of length on units of time: example cm/seg, km/h.
Next we have; the following exercise to calculate the rapidity.
 | Un disco de 30 cm de diámetro, realiza 46 vueltas en dos minutos. Si el movimiento es circular uniforme, calcular la rapidez o módulo de la velocidad tangencial de un punto del borde del disco. |
|---|---|
| Datos. | D = 30 cm (diameter); where R (radio); we have 2 left 15 cm, n = 46 returns, t = min, π = 3,14. |

(Prepared for@coolxxx.)
The Angular speed, in her it describes the circumference of center “ 0 “ with R, whose movements are uniform, in an interval of time giving an angle.
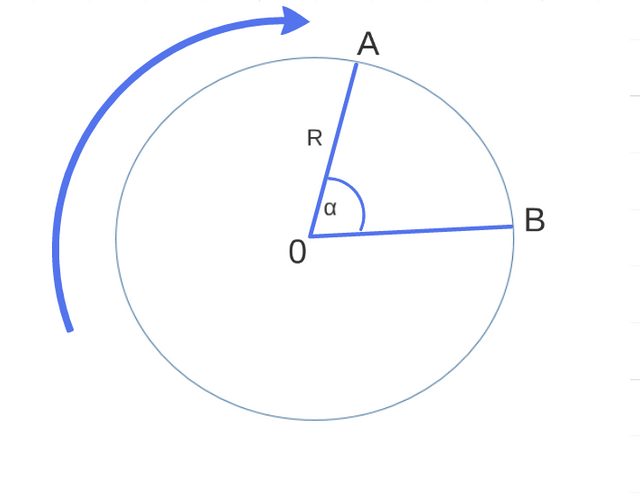
Figure - 2 (Prepared for @coolxxx.)
In this figure we see, in such a way that an arch is described between AB, where an interval of time, from the point A divides up to the place in B, indicating R me remove and it sweeps of the angle. Since α is an angle to the center, it is necessary to think or that must have his apex in the center of the circumference, this way determine that it expires with the following thing, the measurement of the arch is the measurement of the angle in AB.
This angular speed, it measures itself for the quotient between the swept angle, for I remove in an interval of time.
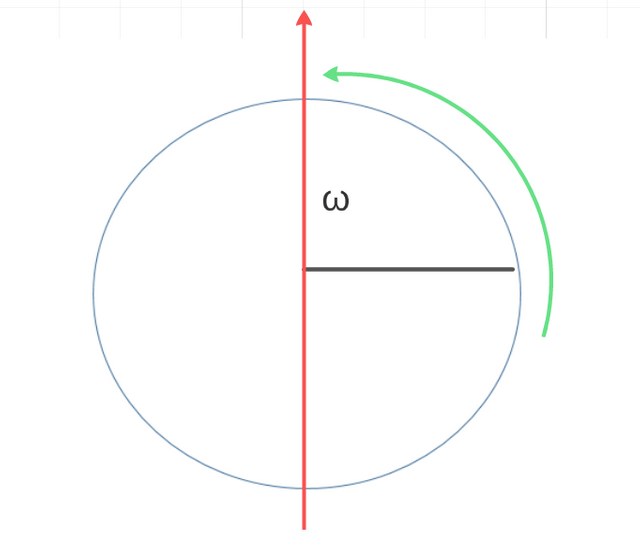
Figure - 3 (Prepared for@coolxxx.)
We can observe as it is the magnitude vectorial, where the direction is the axis of rotation.
We have the angular speed left:
ω = α/t
I could measure in revolutions where 1 = 360th, bearing in mind the length of a circuferencia = 2πR.
α = 2πR/R (rad).
α = 2 π.
ω = 2 π. n / t.
Next we have the following exercise.
 | A body that describes one circumferences with circular uniform movement, where it realizes 360 returns in 3 minutes. It is desirable to know what the angular speed is. |
|---|---|
| Datos. | n= 360 returns, t= 3 min, ω =? |

(Prepared for@coolxxx.)
Observation.
If we compare the equations of rapidity and that of angular speed, they keep great relation since, the physical phenomenon as for this circular movement, where a body his speed turns about his fixed axis, with the same speed for all the point in they and his speed module is going to depend on a point, in distance to his axis of rotation.
| Relation | Equations |
|---|---|
| The Rapidity | V= 2πR . n / t |
| The Speed | ω = 2π . n / t |
We realize the following thing; we place two equations, member divides his member:
(The Vth = 2πR. n / t) / (ω = 2 π. n / t.)
We have left:
V/ω = R, we clear the Vth; we have the following equation left.
V = ω .R.
This relation of equation, it shows us that the product of the angular speed, for the radio it is equal to the tangential module, in a circular uniform movement.
Next the following exercise, to explain better this relation of equation.
 | Un athlete pitcher of Olympian bullet, in his movement describes a circumference of a radio of 1 m, of a uniform way, with an angular speed of 2200 rev/min. To calculate the rapidity. |
|---|---|
| Datos. | R= 1 mts, ω = 2200 rev/min, V=? |

(Prepared for@coolxxx.)
I conclude with the following thing, considering the movement to be a physical phenomenon, the physics tackles in different his branches linked to her, as the kinematics, as one of the general branches also, his application in the Mechanics, having different fields of application, analyzing rectilinear, parabolic, circular movements, since in our daily life we experience it every day.
Source bibliographical:
I
ntroduction to the concepts and theories of the physical sciences for Gerald James Holton, Stephen G. Brush (1996).
Physics for Raymond A. Serway, Jerry S. Faughn (2001).
Questions and problems of essentials of physics for Juan I. Mengual, María of the Peace Godino, Mohamed Khayet (2004).
Physics Volume l (2006).

Buen trabajo compañero @coolxxx soy amate de la física y la ciencia, gracias por mostrar un ejemplo de la ecuación y el valor angular dentro de movimiento circular.