Some Curves Are Just Better Than Others: Bitcoin’s Elliptic-curve cryptography

Cryptography is the art and science of storing and communicating data securely among an antagonist agent who may or may not be actively trying to intersect the original data for malicious purposes. Put simply, cryptography allows information to be communicated and kept in secret. Cryptography is closely linked to the disciplines of cryptology and cryptanalysis.

Under the umbrella of cryptography resides two main branches:
I. Encryption:
Encryption is the process of using an algorithm to transform data/information into an unreadable format for whom it was not intended for.
Symmetric-key encryption is one of the oldest types of encryption and makes use of the same key to both encrypt and decipher sensitive information. In order to read messages , the sender and receiver would need to know the secret key ahead of time. This is one of the weaknesses of symmetric encryption, in that the ability to share the one key in a secure channel is not always possible, a vulnerability that one cannot be exposed to within the Bitcoin Blockchain network. Without the use of this type of encryption, trust is an element/foundation that would have lacked for making the bitcoin network a trusted operation.

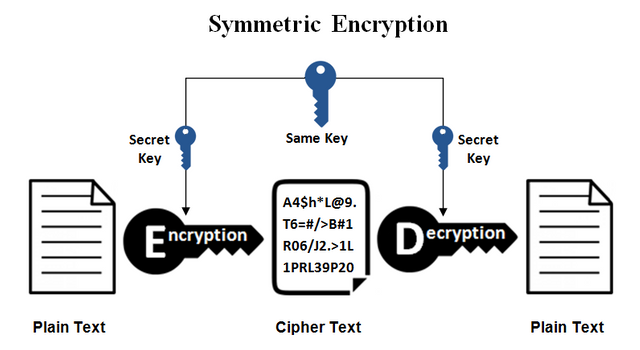
The bitcoin blockchain does not make use of symmetric encryption as all transactions are broadcast and can be seen by anyone. What it does make use of is public key cryptography/asymmetric cryptography to handle transactions.
Public-key cryptography makes use of two types of keys, private and public.

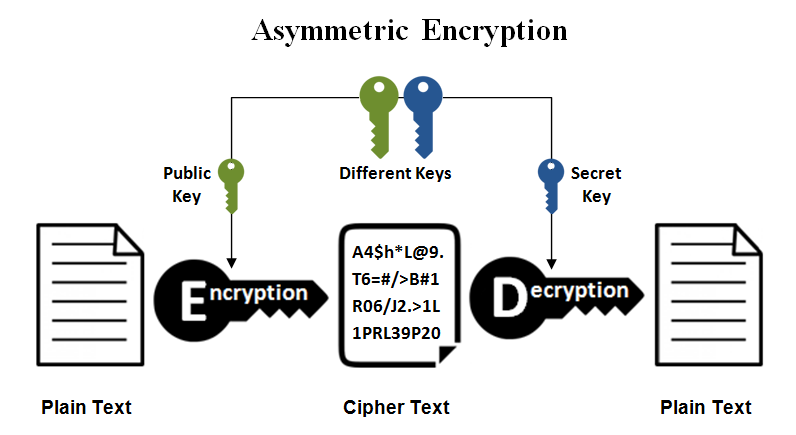
II. Digital Signatures (asymmetric cryptography):
Digital signatures are a mathematical techniques used to validate the authenticity and integrity of a message, software, and digital software or in this case, transactions.
There are two main functionalities that are required from digital signatures, being:

1. Only you can create your signature, however anyone of interest should be able to verify it.
2. The signature must be linked to a specific transaction.

Three important operations that should be able to be performed by digital signatures:

1. Generate keys operations:
   Generates two keys, a private signing key which is not to be revealed to anyone, which is used to create your signature, and a public key which is used for verification purposes, which is going to be given to anyone on the network, of which they will use it to verify your signature.

2. Sign operation:
   You make use of your private key, which is used to sign your messages/transaction which returns your signature.

3. Verification operations:
   Takes something that claims to be a valid signature and verifies that its correct. I takes the public key of the signer, it takes the message that the signature is on and it takes the signature and determines whether it’s valid or not, true or false.

There are three main public key classes used:

1. Integer factorization: It’s an algorithm used secure public-key encryption systems.
2. Discrete logarithm : Based on the intractability of the discrete logarithm problem
   on finite cyclic groups. It was introduced in 1976 by Diffie and Hellman.
3. Elliptic-curve cryptography:
   ECDSA (Elliptic Curve Digital Signature Algorithm) is a cryptographic algorithm used by Bitcoin to ensure that funds can only be spent by their rightful owners. ECDSA uses an elliptic curve to sign transactions on the bitcoin blockchain while making it possible for known/unknown parties of interest to verify the authenticity and integrity of transactions by e.g miners.
   NB: Concepts related to ECDSA are: 1.Private key 2.Public key 3.Signature

///////////////////////////////// Contacts: quantsplayground@gmail.com //////////////////////////////////////

Below is some basic mathematics and concepts in order to refresh yourself with regards to the functionality of Elliptic-curve cryptography:

1. Algebraic structures of groups, rings, and fields.
   1.1 Groups
   A group G is a finite or infinite set of elements together with a binary operation which together satisfy the four fundamental properties of closure, associativity, the identity property, and the inverse property. The operation with respect to which a group is defined is often called the “group operation,” and a set is said to be a group “under” this operation

1.2 Abelian Groups
Abelian groups are groups where all elements in that group commute. Another important type of group is the cyclic group. Cyclic groups have at least one element g, the powers of which run through all the elements in the group. The element g is called a generator.
2.Rings
A ring is a set S together with two binary operators + and ∗ (addition and multiplication, respectively) satisfying the following conditions:
-1. Additive associativity
-2. Additive commutativity
-3. Additive identity
-4. Additive inverse
-5. Multiplicative associativity
-6. Left and right distributivity

3.Fields
A field is any set of elements which satisfies the field axioms for both addition and multiplication and is a commutative division algebra.
3.1 Finite Fields
A finite field is a field with a finite number of elements, also called a Galois field. The order of a finite field is always a prime or a power of a prime.

4.Modular Arithmetic
Modular arithmetic (sometimes referred to as clock arithmetic) is much easier to work with than the “standard” arithmetic we generally use. This system is based in the notion of congruence and residue classes.

1. Modular Arithmetic
   Modular arithmetic is that it complies with the same axioms as the standard arithmetic we’re used to. To explain this, one must understand the notion of congruences and residues.