Finding the Height of a Distant Island: Can you solve this 1800-year old math problem?

I'm still officially on vacation, but I thought I'd post anyways today.

For Chinese-speaking communities around the world, today is the Qingming Festival, or the "Tomb Sweeping Festival". On this day, people will visit the graves of their ancestors to tidy them up and to offer prayers on their behalf. After this, people will often celebrate by going on family outings.

A famous painting from the Northern Song dynasty (920-1126 CE) depicts a festive scene in the city of Kaifeng, then known as Bianjing. The scroll Along the River During the Qingming Festival (清明上河圖) measures about 5.25 metres long, and contains 814 humans, 28 boats, 60 animals, 30 buildings, 20 vehicles, 8 sedan chairs, and 170 trees [1].

Click here to see larger version. Source: National Palace Museum (Taipei)

In the rightmost section of a 18th-century Qing Dynasty remake of the painting, we see a boat in the distance, perhaps preparing to dock at a port. This made me recall an some problems from the the Haidao Suanjing (海島算經, literally: "Sea Island Calculation Manual"), an ancient Chinese mathematics text that contains nine problems related to maritime navigation and surveying.

The first of these problems involves determining the height of a remote island at a distance. In Classical Chinese, the text runs:

今有望海島，立兩表，齊高三丈，前後相去千步，令後表與前表參相直。從前表卻行一百二十三步，人目著地取望島峯，與表末參合。從後表卻行一百二十七步，人目著地取望島峯，亦與表末參合。問島高及去表各幾何？

Which in translation (my own reads):

Suppose there exists a distant island. Erect two poles, each with a height of three zhàng, with a space of a thousand paces between them, so that they are in a straight line with the island. When one stands at a distance of 123 paces from the front pole, one sees that its tip coincides with the peak. [Likewise], if one stands at a distance of 127 paces from the rear pole, the tip of the back pole also coincides with the peak. [We ask:] What is the height of the island and its distance from the front pole?

Generalizing this question, we ask ourselves the following: "How can we express h and D in terms of a, d, b₁, and b₂?

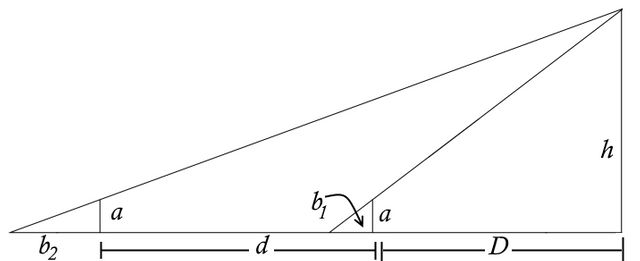
The challenge: Can you come up with a general formulas for the height and the distance?

As always, we strive to find a general formula or method. A numerical answer (which I'll provide anyhow) is not as good as showing how you derived the answer. Hint: The answer involves a combination of similar triangles and binomial factoring.

If you derive the algorithm, and then plug in the numbers, you will obtain a solution of: 4 Ii and 55 paces for the height, and 102 li and 150 paces for the distance. Of course, it is necessary to use the following conversions:

1 li (里) = 1800 feet (尺)
1 zhàng (丈) = 10 feet (尺)
1 pace (步) = 6 feet (尺)