APRENDIENDO A CONSTRUIR UN ESPECTRO DE RESPUESTA ELÁSTICO A PARTIR DE LA EXCITACIÓN SÍSMICA DE SISTEMAS DE UN GRADO DE LIBERTAD. APLICACIONES EN LA INGENIERÍA SISMORESISTENTE
INTRODUCCIÓN
En el presente artículo aprenderemos a construir un espectro de respuesta elástico a partir de los registros de aceleración del terreno (acelerograma) producidos por un sismo. El proceso de construcción de un espectro de respuesta se resume en resolver la ecuación diferencial de equilibrio dinámico del sistema estructural que se analiza para distintos valores de periodos naturales “Tn” que este pueda tomar, dejando constante la fracción de amortiguamiento crítico “ξ”; para así seleccionar las respuestas máximas obtenidas para cada caso de estudio, representados en este artículo por los distintos valores de periodo natural “Tn” que se evalúan en la ecuación diferencial en cuestión, la cual podemos apreciar en la imagen N°01, para de este modo graficar el par de respuesta: periodo natural “Tn” – respuesta máxima, obteniendo como resultado un espectro de respuesta elástico. El término elástico hace referencia al desempeño que tendrá el sistema estructural ante la excitación sísmica.
Conviene señalar que la solución de esta ecuación diferencial de segundo orden, la estaremos realizando con ayuda de la herramienta computacional NONLIN V 7.14, y las respuestas máximas seleccionadas serán en términos de desplazamiento; realizando así la evaluación para tres casos de periodos naturales “Tn” definidos arbitrariamente, y dejando la fracción de amortiguamiento crítico “ξ” constante. Se establecen estos tres puntos, para que el lector se familiarice con el proceso del surgimiento de la información que constituye un “espectro de desplazamiento” y también porque serán tomados como base para el estudio de las expresiones matemáticas (Ec. 17 y Ec. 18), que permiten obtener espectros de “pseudo- velocidad” y “pseudo-aceleración”; realizando un contraste con los resultados de respuesta en términos de “pseudo-velocidad” y “pseudo-aceleración” de los espectros arrojados por la herramienta computacional NONLIN V 7.14, que se ilustran en la imagen N°01.
Imagen N°01: una visión general de los contenidos a estudiar
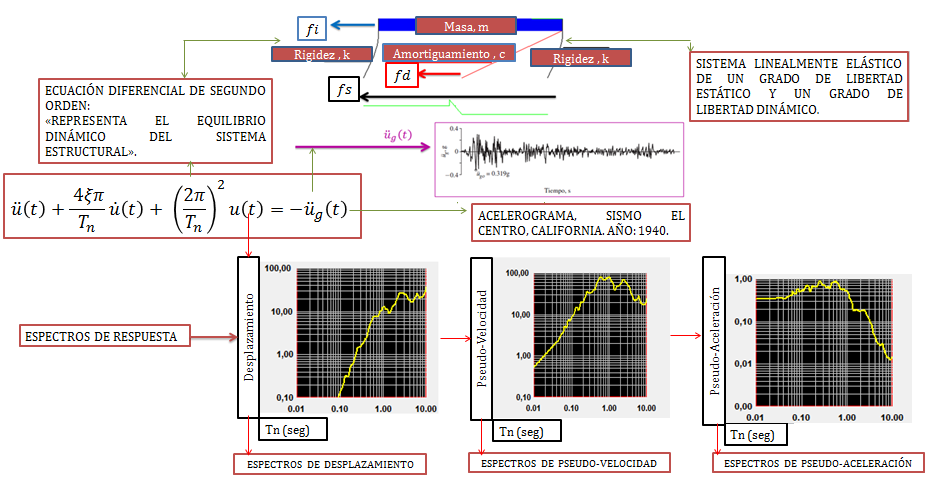
Fuente: Chopra (2014), NONLIN V 7.14, adaptada por Santana (2018)
Una vez que se comprendan los principios en los que se fundamenta la construcción de un espectro de respuesta elástico, se enaltece la utilidad de los mismos con la introducción del concepto de fuerza estática equivalente “Fe”, que representa una simplificación del problema dinámico, a un problema estático, cuya fuerza, que desarrolla la máxima respuesta de la estructura en términos de desplazamiento “umax”, permite obtener los esfuerzos internos de sus elementos; constituyendo esto una de las principales aplicaciones del análisis espectral en el campo de la ingeniería sismoresistente.
DELIMITACIÓN DE LA TEMÁTICA A ESTUDIAR
Estaremos tomando como estructura modelo, un pórtico plano de un grado de libertad dinámico y un grado de libertad estático (ver imagen N°03), el cual se encuentra sometido a una excitación sísmica en su base, y cuya respuesta estructural la vamos a considerar en el rango de comportamiento lineal elástico. Para los fines de este artículo, esta excitación sísmica estará representada por el acelerograma que se muestra en la imagen N°02; al cual se le conoce como “Acelerograma El Centro, California” haciendo referencia a la subestación donde el mismo fue registrado.
Imagen N°02: respuesta en el tiempo del terreno en términos de aceleración. Sismo Valle Imperial, California. Año: 1940
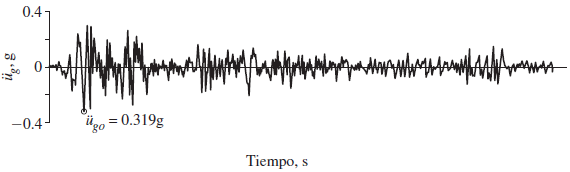
Fuente: Chopra (2014)
Es importante reflexionar lo que experimenta una estructura de un grado de libertad, cuando es sometida a una excitación de este tipo en su base. Este hecho se ilustra en la imagen N°03:
Imagen N°03: sistema estructural sometido a una excitación en la base
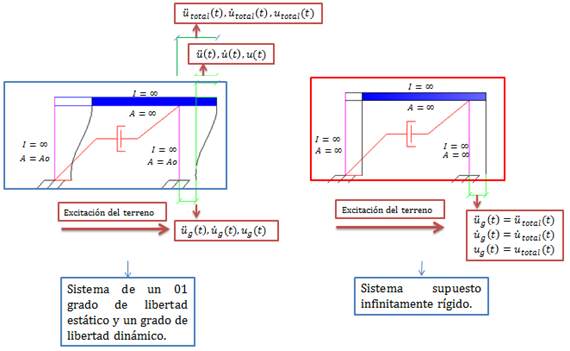
Fuente: Santana (2018)
Notemos que para un sistema infinitamente rígido, resaltado en color “rojo”, caracterizado por poseer elementos estructurales imposibilitados de sufrir deformación axial y transversal, debido a sus propiedades de inercia y de rigidez, al producirse la excitación del terreno, la estructura se mueve como un cuerpo rígido por lo que el desplazamiento del terreno “ug(t)” coincide con el desplazamiento total “utotal(t)”. De acá se desprende una hipótesis de importancia práctica, relativa a visualizar el terreno como un medio rígido y es clave tenerla en cuenta en el proceso de construcción de los espectros.
Ahora bien, en el caso de la estructura resaltada en color “azul”, la cual es el caso de interés con el que estaremos trabajando por el hecho de que es representativa de un sistema de un grado de libertad tanto estático como dinámico, al producirse la excitación del terreno, se plantean adicional a los desplazamientos, velocidades y aceleraciones del mismo “üg(t), ůg(t) y ug(t)”, los desplazamientos, velocidades y aceleraciones de la masa con respecto a la base “ü(t), ů(t) y u(t)”, por lo que los valores totales de cada una de estas variables vienen dado por:
Estas ecuaciones presentadas, sugieren que la función que representa el acelerograma de la imagen N°02, ha de ser integrada una y dos veces, para obtener la respuesta en el tiempo en términos de velocidades y desplazamientos respectivamente, como se muestra en la siguiente imagen:
Imagen N°04: respuesta en el tiempo del terreno en términos de velocidad y desplazamiento. Sismo Valle Imperial, California. Año: 1940
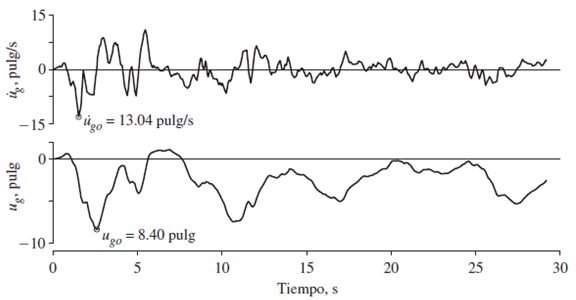
Fuente: Chopra (2014)
El desplazamiento total al cual se hace referencia en la ecuación N°03, resulta de especial interés para establecer la separación adecuada entre dos estructuras, y evitar el choque de las mismas ante la ocurrencia de un sismo. Sin embargo, en este artículo centraremos la atención en el desplazamiento relativo que experimenta la masa con respecto a la base, responsable del surgimiento de esfuerzos internos en los elementos estructurales; desplazamiento que es posible obtener gracias a la solución numérica de la ecuación diferencial de equilibrio dinámico, cuyo planteamiento se desarrolla a continuación.
Imagen N°05: planteamiento de la ecuación diferencial de equilibrio dinámico
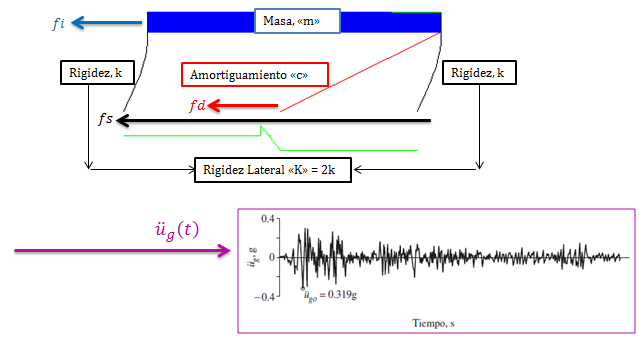
Fuente: Chopra (2014) adaptada por Santana (2018)
Se aprecia en la imagen N°05, que al producirse la excitación del terreno, la estructura responde en base a sus componentes de masa “m”, amortiguamiento “c” y rigidez “k”, por medio de fuerzas inerciales “fi”, fuerzas de amortiguamiento “fd” y fuerzas de restitución elásticas “fs” para devolver el sistema a su posición de equilibrio. Dado que la excitación en la base, está representada en esencia por una aceleración del terreno que varía con el tiempo “acelerograma”, y la masa “m” experimenta una aceleración con respecto a la base (ver imagen N°03), la fuerza inercial se puede expresar de la siguiente manera:
Por su parte, para los fines de este artículo, las fuerzas de amortiguamiento “fd” y de restitución elástica “fs” las podemos expresar en función de la velocidad y el desplazamiento relativo de la masa con respecto a la base, de la forma:
Al ensamblar las ecuaciones N°04, N°05 y N°06, obtenemos la ecuación diferencial de equilibrio dinámico del sistema:
Rescribimos la ecuación N°07 y obtenemos:
La solución de la ecuación diferencial de equilibrio dinámico del sistema, la estaremos obteniendo con la herramienta computacional NONLIN V 7.14, donde la excitación del terreno estará representada por el acelerograma de la imagen N°02; a continuación se muestra como esta función sísmica es incluida en el programa en cuestión:
Imagen N°06: incorporación de la función sísmica en el programa NONLIN V 7.14
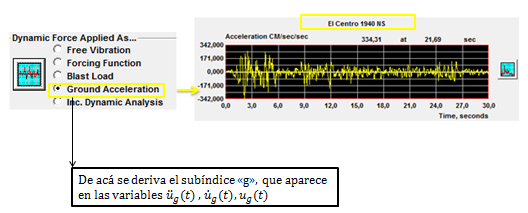
Fuente: NONLIN V 7.14 adaptada por Santana (2018)
A continuación procedamos a realizar un planteamiento alternativo de dicha ecuación, con la finalidad de enfatizar la responsabilidad de las propiedades dinámicas de la estructura, especialmente el periodo natural “Tn” y la fracción de amortiguamiento crítico “ξ” en la respuesta a obtener. Se recomienda al lector la revisión de la referencia N°03 para que profundice en tales propiedades.
PLANTEAMIENTO ALTERNATIVO DE LA ECUACIÓN DIFERENCIAL DE EQUILIBRIO DINÁMICO
La ecuación N°08 puede ser rescrita en función de propiedades dinámicas de fácil determinación en la estructura que se analiza, correspondientes al periodo natural “Tn” y fracción de amortiguamiento crítico “ξ”. Para tal fin, planteemos las siguientes relaciones básicas:
Dividamos en primera instancia la ecuación N°08 entre la masa “m” de la siguiente forma:
Reescribimos la ecuación N°12:
Sustituimos la ecuación N°11 en la ecuación N°13:
Reescribimos:
Finalmente sustituimos la ecuación N°10 en la ecuación N°15:
De acuerdo a lo mostrado en la ecuación N°16 la respuesta estructural está condicionada al periodo natural “Tn” y a la fracción de amortiguamiento crítico “ξ” de la estructura. Tal como se señaló en líneas anteriores, la solución de esta ecuación diferencial de segundo orden, la estaremos llevando a cabo con ayuda de la herramienta computacional NONLIN V 7.14, siendo esta solución para distintos valores de periodo “Tn” y una fracción de amortiguamiento crítico “ξ” constante, la base para la construcción del espectro de respuesta elástico para sistemas de un grado de libertad.
CONSTRUYENDO EL ESPECTRO DE RESPUESTA ELÁSTICO EN TÉRMINOS DE DESPLAZAMIENTO CON AYUDA DE LA HERRAMIENTA COMPUTACIONAL NONLIN V 7.14
Es muy importante definir lo que es un espectro de respuesta, según Chopra (2014):
Es una gráfica del valor máximo de una cantidad de respuesta como una función del período de vibración natural “Tn” del sistema, o de un parámetro relacionado, como la frecuencia circular “ωn” o la frecuencia cíclica “fn”.
Partiendo de esta premisa, realizaremos con ayuda de la herramienta computacional NONLIN V 7.14 la solución numérica de la ecuación N°16, delimitándonos a la evaluación de tres periodos naturales “Tn” y dejando fija la fracción de amortiguamiento crítico “ξ”; seleccionando en cada evaluación el valor máximo de respuesta en términos de desplazamiento, y así construir el respectivo espectro de respuesta.
Dado que se requiere ingresar en la herramienta computacional NONLIN V 7.14 diversos valores de periodo natural “Tn”, tomando como referencia la estructura de la imagen N°05, estableceremos arbitrariamente diversos valores de rigidez “K” y masa “m” para lograr tal fin, para lo cual se utilizan las ecuaciones N°09 y N°10. Por lo que es oportuno plantear la siguiente tabla:
Tabla N°01: valores arbitrarios de “K” y “W” para el establecimiento de diversos periodos naturales “Tn”

Fuente: Santana (2018)
En cuanto a la fracción de amortiguamiento crítico “ξ” tomaremos un valor en el orden del 5%, para las evaluaciones numéricas a realizar. Procedamos a incluir cada uno de estos datos en la herramienta computacional NONLIN V 7.14.
Para el caso N°01 se tiene:
Imagen N°07: respuesta de desplazamiento en el tiempo para: Tn=0.20 seg y ξ=5%
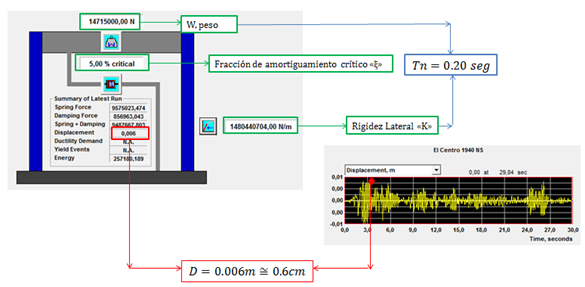
Fuente: NONLIN V 7.14 adaptada por Santana (2018)
Para el caso N°02:
Imagen N°08: respuesta de desplazamiento en el tiempo para: Tn=0.30 seg y ξ=5%
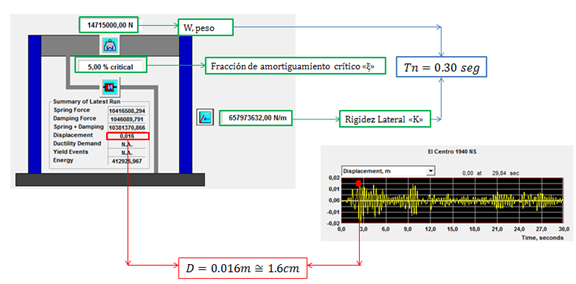
Fuente: NONLIN V 7.14 adaptada por Santana (2018)
En lo que respecta al caso N°03:
Imagen N°09: respuesta de desplazamiento en el tiempo para: Tn=1.00 seg y ξ=5%
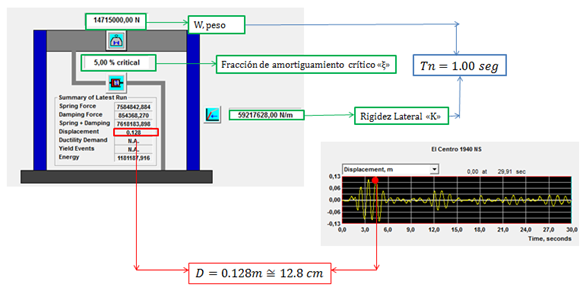
Fuente: NONLIN V 7.14 adaptada por Santana (2018)
Una vez obtenida las respuestas máximas en términos de desplazamiento, para cada valor de período natural “Tn”, se procede a graficar estos valores obteniendo el espectro de respuesta de desplazamiento. Es evidente que para su construcción se requieren muchos más puntos que los evaluados a lo largo de las imágenes N°07, N°08 y N°09. Sin embargo, lo realizado es para familiarizar al lector de un modo didáctico con el proceso de cálculo involucrado en este tema. En aras de complementar la idea, se presenta a continuación el espectro de desplazamiento, que proporciona el programa NONLIN V 7.14:
Imagen N°10: espectro de desplazamiento, ξ=5%
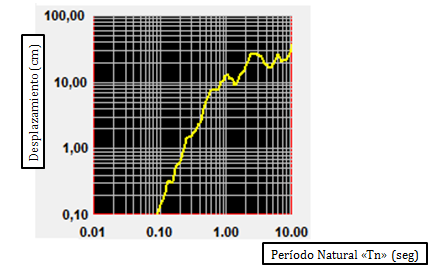
Fuente: NONLIN V 7.14, adaptada por Santana (2018)
Ahora bien, los tres valores de período natural “Tn” evaluados a lo largo de las imágenes N°07, N°08 y N°09 serán base para el abordaje crítico reflexivo que se realizará para las fórmulas empleadas utilizadas en la obtención de los espectros de “pseudo-velocidad” y “pseudo-aceleración”, a partir del espectro de desplazamiento.
ABORDAJE CRÍTICO REFLEXIVO DE LAS FÓRMULAS EMPLEADAS PARA OBTENER EL ESPECTRO DE PSEUDO-VELOCIDAD Y PSEUDO-ACELERACIÓN
Conviene señalar que el prefijo “pseudo” es para enfatizar que los valores de velocidad y aceleración que constituyen tales espectros, son obtenidos indirectamente a partir de las respuestas máximas en términos de desplazamiento. Para tal fin existen las siguientes relaciones muy prácticas y sencillas de utilizar:
El valor de “pseudo-aceleración” en los espectros se suele expresar como una fracción de la gravedad, lo que da la bienvenida al concepto de aceleración espectral “Ad”:
Para cada uno de los desplazamientos máximos obtenidos en las imágenes N°07, N°08 y N°09, aplicamos estas ecuaciones, obteniendo lo siguiente:
Tabla N°02: obtención de valores de “pseudo-velocidad” y “pseudo-aceleración”
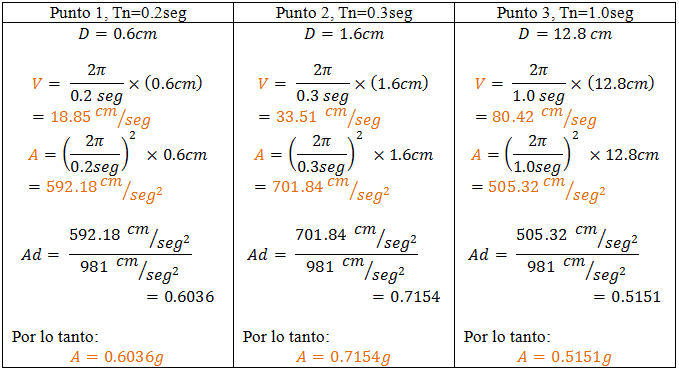
Fuente: Santana (2018)
Ahora bien, en aras de realizar un abordaje crítico reflexivo de las ecuaciones N°17 y N°18, los valores obtenidos en la tabla N°02 en cuanto a “psuedo-velocidad - V” y “pseudo-aceleración - A”, procederemos a contrastarlos con los valores provenientes de los espectros, que nos proporciona la herramienta computacional NONLIN V 7.14.
Imagen N°11: espectro de “pseudo-velocidad”, ξ=5%
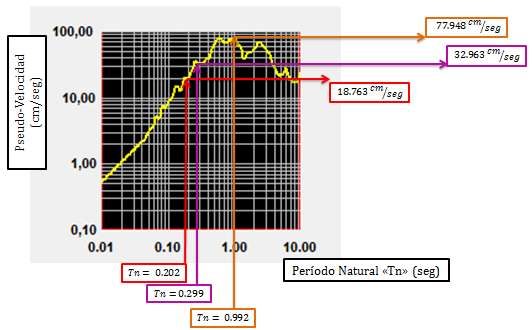
Fuente: NONLIN V 7.14 adaptada por Santana (2018)
Los períodos con los cuales se ingresó en el gráfico de la imagen N°11, son aproximadamente iguales a los períodos naturales “Tn” presentados en la tabla N°02, por lo que procedemos a realizar una comparación con los resultados obtenidos aplicando la ecuación N°17, de la siguiente manera:
a.- Para período de 0.202 seg ≈ 0.20 seg
En términos porcentuales la diferencia fue de:
b.- Para período de 0.299 seg ≈ 0.30 seg
En términos porcentuales la diferencia fue de:
c.- Para período de 0.992 seg ≈ 1.00 seg
En términos porcentuales la diferencia fue de:
Se aprecian unas diferencias porcentuales entre los valores de “pseudo-velocidad” menor al 5%, lo que demuestra la utilidad práctica de la ecuación N°17.
Imagen N°12: espectro de “pseudo-aceleración”, ξ=5%
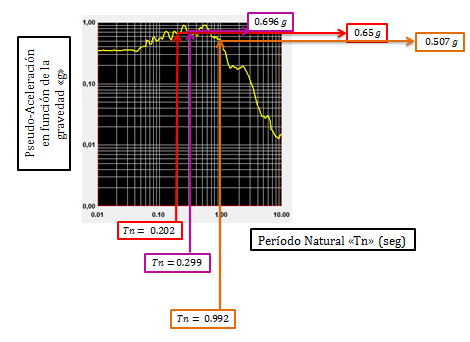
Fuente: NONLINV 7.14 adaptada por Santana (2018)
Los períodos con los cuales se ingresó en el gráfico de la imagen N°12, son aproximadamente iguales a los períodos naturales “Tn” presentados en la tabla N°02, por lo que procedemos a realizar una comparación con los resultados obtenidos aplicando la ecuación N°18, de la siguiente manera:
a.- Para período de 0.202 seg ≈ 0.20 seg
En términos porcentuales la diferencia fue de:
b.- Para período de 0.299 seg ≈ 0.30 seg
En términos porcentuales la diferencia fue de:
c.- Para período de 0.992 seg ≈ 1.00 seg
En términos porcentuales la diferencia fue de:
A modo de análisis crítico reflexivo, podemos señalar que los resultados de “pseudo-velocidad” y “pseudo-aceleración” obtenidos con la aplicación de las ecuaciones N°17 y N°18 respectivamente, presentan una cercanía bastante aceptable con los obtenidos directamente con el uso de la herramienta computacional NONLIN V 7.14. En la mayoría de los casos evaluados la diferencia porcentual es menor al 5%. Es claro que las ecuaciones N°17 y N°18 nos dan valores aproximados, pero su utilidad práctica para ahorrar proceso de cálculo numérico, al momento de querer pasar de un tipo de espectro de respuesta a otro, es de mucho interés en el campo de la ingeniería sismoresistente.
INTRODUCCIÓN AL CONCEPTO DE FUERZA ESTÁTICA EQUIVALENTE
En el análisis espectral que se viene desarrollando, partimos de la hipótesis de que el terreno de fundación es un medio rígido. De lo que se desprende, que el comportamiento del terreno no está influenciado por el comportamiento de la estructura. Tal suposición, permite idear al pórtico plano de un grado de libertad de la imagen N°13, con una base fija, y que ante la excitación del terreno producto de un sismo, experimenta un desplazamiento relativo de la masa con respecto a la base.
Imagen N°13: pórtico plano supuesto con base fija, sometido a una excitación del terreno
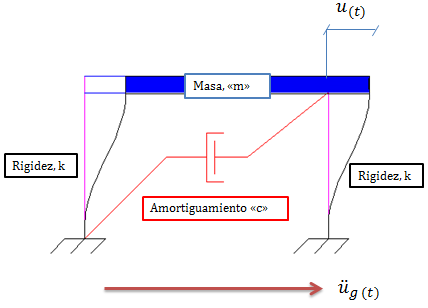
Fuente: Santana (2018)
Dado que es el desplazamiento relativo de la masa con respecto a la base, lo que produce solicitaciones internas en los elementos estructurales, se puede plantear un sistema estático equivalente con una fuerza “Fe” aplicada en la masa, que produzca el mismo desplazamiento que el problema dinámico.
Imagen N°14: sistema estático equivalente
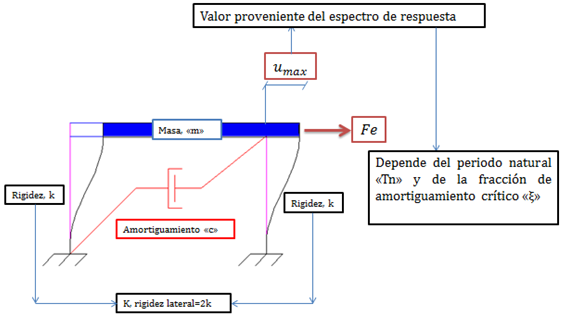
Fuente: Santana (2018)
Esta fuerza “Fe”, es conocida como fuerza estática equivalente. Dado que la rigidez lateral “K” es conocida, se puede plantear la siguiente relación:
En base a la ecuación N°09 la rigidez lateral “K” se puede expresar como:
Al sustituir la ecuación N°21 en la ecuación N°20 se tiene:
El término resaltado en color “naranja” de la ecuación N°22, aparece descrito en la ecuación N°18 y corresponde al valor de “pseudo-aceleración - A”, por lo que esta ecuación se rescribe de la siguiente manera:
Dividimos y multiplicamos por la gravedad:
Rescribimos:
Dónde:
W, es el peso
Ad, es la aceleración espectral, y según Chopra (2014):
Puede interpretarse como el coeficiente sísmico o el coeficiente de fuerza lateral. Se utiliza en los códigos de construcción para representar el coeficiente por el cual se multiplica el peso de la estructura para obtener la fuerza cortante basal.
Esta fuerza cortante basal “Vb” se obtiene por equilibrio estático, y es opuesta a la fuerza estática equivalente “Fe”, como se ilustra en la siguiente imagen:
Imagen N°15: planteamiento del equilibrio estático
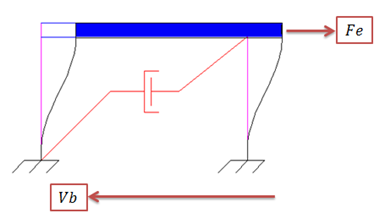
Fuente: Santana (2018)
Conocidas estas solicitaciones, es posible determinar las fuerzas internas que actúan en los elementos estructurales; conviene resaltar que en el proceso de determinación de las mismas el conocimiento de las propiedades dinámicas de la estructura es fundamental, especialmente el periodo natural “Tn” y la fracción de amortiguamiento crítico “ξ”, por lo que se recomienda al lector la revisión de las referencias N°03 y N°04.
CONCLUSIONES
La obtención de los espectros de respuesta a partir de un acelerograma permite el desarrollo de una herramienta muy valiosa en el análisis sismoresistente de una edificación. Sin embargo, no siempre se cuenta con registros de acelerogramas, por lo que se han desarrollado lo que se conoce como espectros de diseño, cuya interpretación de la información que contienen, es en esencia, la misma de los espectros de respuesta. La diferencia fundamental estriba en su proceso de construcción, dado que los espectros de diseño, son construidos en base a parámetros que estandarizan en cierto modo, la excitación del terreno para distintas zonas, en base a la historias de sismos ocurridos. En un próximo post, profundizaré sobre este tipo de espectros ajustado a la norma sísmica venezolana COVENIN 1756:2001; para lo cual es importante el aprendizaje logrado en este trabajo, que a modo de conclusiones se resume en:
1.- Los espectros están constituidos por valores de respuestas máximas, en términos de desplazamiento, velocidad y aceleración.
2.- Son los desplazamientos relativos de la masa con respecto a la base, lo que produce solicitaciones internas en los elementos estructurales.
3.- La aceleración espectral “Ad” es también conocida como coeficiente sísmico.
4.- Los espectros de respuesta son construidos a partir de un acelerograma.
5.- La construcción de un espectro de diseño obedece a parámetros estandarizados, en base a la historia de sismos en un determinado lugar.
En definitiva, el análisis espectral constituye una valiosa herramienta en la proyección y evaluación de edificaciones desde el enfoque de la ingeniería sismoresistente, y es una fiel demostración de los grandes aportes de las Matemáticas a la Dinámica Estructural.
REFERENCIAS CONSULTADAS
1.- CHOPRA ANIL K. 2014. DINÁMICA DE ESTRUCTURAS. CUARTA EDICIÓN. PEARSON EDUCACIÓN, MÉXICO.
2.- NONLIN “EDUCATIONAL PROGRAM FOR LEARNING THE CONCEPTS OF STRUCTURAL DYNAMICS AND EARTHQUAKE ENGINEERING”. DEVELOPED BY DR. FINLEY CHARNEY, NONLIN IS AVAILABLE AS ONLINE TOOL THROUGH NEESHUB: HTTP://NEES.ORG/
3.- SANTANA E. 2018. COMPRENDIENDO LAS APLICACIONES DE LAS MATEMÁTICAS EN LA ESTIMACIÓN DEL PERIODO Y FRECUENCIA NATURAL DE UN PÓRTICO PLANO. CASO: SISTEMA DE UN GRADO DE LIBERTAD. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/comprendiendo-las-aplicaciones-de-las-matematicas-en-la-estimacion-del-periodo-y-frecuencia-natural-de-un-portico-plano-caso
4.- SANTANA E. 2018. DETERMINACIÓN EXPERIMENTAL DEL AMORTIGUAMIENTO EN ESTRUCTURAS. UN ENFOQUE MATEMÁTICO CON APLICACIONES EN LA INGENIERÍA SISMORESISTENTE. DISPONIBLE EN:https://steemit.com/stem-espanol/@eliaschess333/determinacion-experimental-del-amortiguamiento-en-estructuras-un-enfoque-matematico-con-aplicaciones-en-la-ingenieria
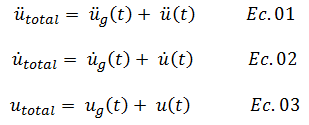
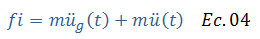
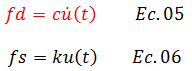
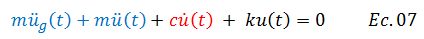
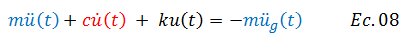
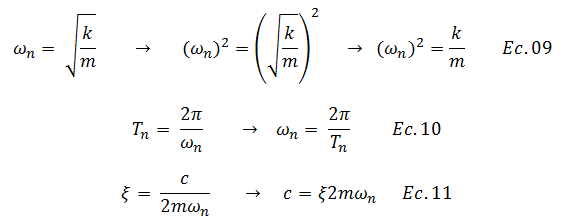
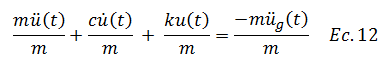
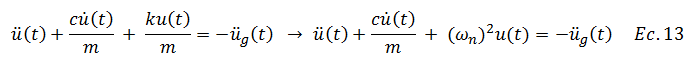
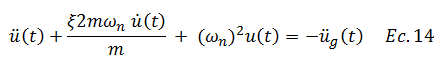
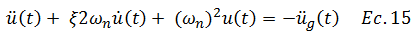
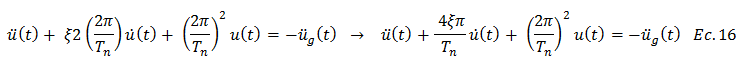
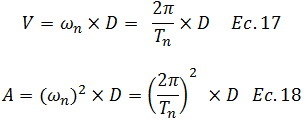
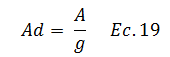
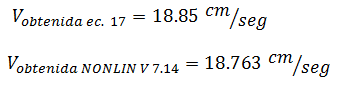
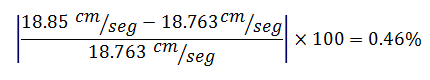
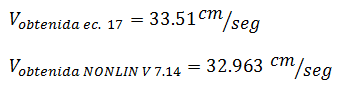
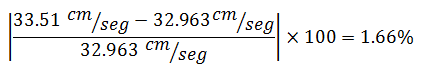
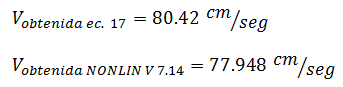
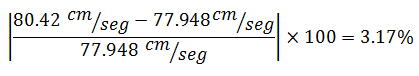
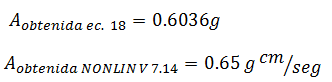
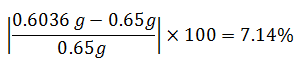

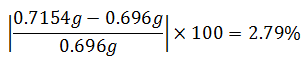
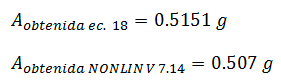
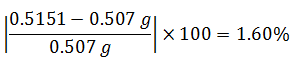
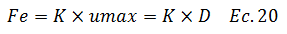
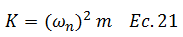
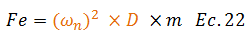
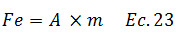
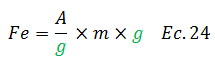
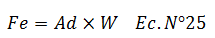
Hola estimado @elisaschess333 tengo una pequeña duda desde hace tiempo con tus artículos y es la siguiente: ¿ de donde obtienes las imágenes? ¿de algún libro, programa o pagina web? se muy bien que mencionas los autores pero es importante conocer si dichas imágenes son libres de derechos de autor. Creo que hace tiempo mencionaste que SANTANA eres tu cierto? pero me gustaría aclarar esta situación.
Saludos cordiales!!
Saludos estimado @carloserp-2000, en efecto mi nombre es Elías Santana, de allí a que en las citas aparezca mi apellido. Las imágenes utilizadas procuro que sean en su totalidad provenientes de referencias bibliográficas, capturas de pantalla de los programas que uso, y las mismas al realizarle una determinada edición, como por ejemplo cuando las utilizo dentro de un mapa conceptual creado por mí, suelo utilizar el siguiente formato:
Autor, autores (referencia bibliográfica o programa utilizado de donde proviene la captura de pantalla), adaptada por Santana (año).
He estado muy al tanto de los cuidados que se deben tener por las imágenes obtenidas de la web, lo cual tendré presente al momento de utilizar una de ellas.
Complacido @carloserp-2000, de pertenecer a esta maravillosa comunidad científica como lo es #stem-espanol, y comprometido de aportar al crecimiento y fortalecimiento de la misma con publicaciones de calidad en mis áreas de formación académica como lo son la ingeniería sismoresistente y la ingeniería geotécnica.
Saludos cordiales!!!
Gracias por aclarar en próximas publicaciones seria bueno que dejaras el enlace de origen de cada imagen, recuerda que existen algunas que no se pueden modificar o reutilizar
Perfecto @carloserp-2000. En el caso de las imágenes que utilizo directamente de un libro o a través de captura de pantalla de un programa, dejaré la referencia del libro o del programa en cuestión. Saludos!
Felicitaciones @eliaschess333 por este post que nos ilustra respecto al uso de las TIC para acometer investigaciones. Éxitos.
Gracias @tomastonyperez. El uso de las tecnologías de información y comunicación nos permite hacer docencia más allá de los muros del aula. Saludos y Éxitos para ti también!