Learn you an AI for great justice - wtf is homomorphic encryption?
Learn you an AI for great justice - wtf is homomorphic encryption?
You will need to make use of all these lessons I promise - you'll put salt in your coffee (if you don't get the joke, reference the previous article).
Previously I promised encryption, madness, pain, death and tentacled abominations and here I shall deliver on the encryption, the madness and the sadness.
In order to enjoy this fully, please listen to the following song, the album it comes from has a fair amount of death and pain and hints at tentacled abominations:
Shut up Gareth and get to the point
Ok, homomorphic encryption: homo means "same", morphic comes from morph meaning "shape". Homomorphic encryption is basically a way to perform operations to a ciphertext that are reflected in the underlying plaintext.
Let's do an example with the world's crappiest encryption algorithm, don't make your message too long or it'll crash - it's that crappy - this is naturally in Python 2.7, but it will eventually be in C - not in this article though, probably on github or elsewhere - and there's a reason for that.
Please note that under no circumstances should you ever use a homebrew cryptosystem for real sensitive data - you are not smart enough. You are smart enough to invent a system that you can't crack, that is easy - but there is always someone smarter than you.
Dabble not with the great old ones, for their cryptographic powers lie outside our reality - only a fool will invoke their wrath with DIY crypto.
Here's the source:
import hashlib
import base64
key = raw_input('Enter key:').strip('\n')
plaintext = raw_input('Enter message:').strip('\n')
h = hashlib.sha512(key).digest()
retval = ''
for i in xrange(len(plaintext)):
retval += chr(ord(plaintext[i])^ord(h[i]))
print base64.b64encode(retval)
gareth@skynet:~/steem_posts$ python encrypt.py
Enter key:1234
Enter message:Testing
gGEm6wlAzA==
And here's how we decrypt it:
import hashlib
import base64
key = raw_input('Enter key:').strip('\n')
ciphertext = base64.b64decode(raw_input('Enter message:').strip('\n'))
h = hashlib.sha512(key).digest()
retval = ''
for i in xrange(len(ciphertext)):
retval += chr(ord(ciphertext[i])^ord(h[i]))
print retval
gareth@skynet:~/steem_posts$ python decrypt.py
Enter key:1234
Enter message:gGEm6wlAzA==
Testing
This system is NOT homomorphic.
In order to make it homomorphic we can do something fairly simple: we replace that XOR with a + in the encrypt.py script and then use - in the decrypt.py script. Since the result will often exceed the range of ASCII characters we use my old favourite friend msgpack to store the numeric values.
Here's the new code and the output:
import hashlib
import msgpack
import base64
key = raw_input('Enter key:').strip('\n')
plaintext = raw_input('Enter message:').strip('\n')
h = hashlib.sha512(key).digest()
retval = []
for i in xrange(len(plaintext)):
retval.append(ord(plaintext[i])+ord(h[i]))
retval = msgpack.packb(retval)
print base64.b64encode(retval)
gareth@skynet:~/steem_posts$ python encrypt.py
Enter key:1234
Enter message:Testing
l80BKGnMyM0BE8zJzJzNARI=
Now let's do a magic trick: we'll turn the string "TESTING" into "testing" without decrypting it. Doing this is actually quite easy - to convert any ASCII character into uppercase we simply subtract 32 from it and vice versa.
As an example, the letter a when lowercase has ASCII code 97, the uppercase A is 65. Subtract 32 from 97 and you get 65.
First, let's encrypt our string "TESTING" with the key 1234, this yields the base64 l80BKEnMqMzzzKl8zPI= which we can then decode and perform addition on it.
I created a script named homotest for this. I'm not sure why people are giggling, but let's move on. Here's the code and an example of me running the code:
import hashlib
import msgpack
import base64
ciphertext = base64.b64decode(raw_input('Enter message:').strip('\n'))
ciphertext = msgpack.unpackb(ciphertext)
retval = []
for i in xrange(len(ciphertext)):
retval.append(ciphertext[i]+32)
retval = msgpack.packb(retval)
print base64.b64encode(retval)
gareth@skynet:~/personality_tests$ python homotest.py
Testing who? Gareth Nelson
Only for John Barrowman
err, sorry - that's the wrong homotest (but on a sidenote have you seen Barrowman? I would hit that - if this humour offends you then you're in totally the wrong place)
Here's the correct one:
gareth@skynet:~/steem_posts$ python homotest.py
Enter message:l80BKEnMqMzzzKl8zPI=
l80BSGnMyM0BE8zJzJzNARI=
Let's decrypt that now to see if the magic worked, code and execution results below:
import hashlib
import msgpack
import base64
key = raw_input('Enter key:').strip('\n')
ciphertext = base64.b64decode(raw_input('Enter message:').strip('\n'))
ciphertext = msgpack.unpackb(ciphertext)
h = hashlib.sha512(key).digest()
retval = []
for i in xrange(len(ciphertext)):
retval.append(chr(ciphertext[i]-ord(h[i])))
print ''.join(retval)
First, the original message (TESTING) before we did the transforms (look at homotest.py again - no key is taken!):
gareth@skynet:~/steem_posts$ python decrypt.py
Enter key:1234
Enter message:l80BKEnMqMzzzKl8zPI=
TESTING
Now the transformed message:
gareth@skynet:~/steem_posts$ python decrypt.py
Enter key:1234
Enter message:l80BSGnMyM0BE8zJzJzNARI=
testing
There's nothing stopping us from doing this in reverse - just subtract 32 instead of adding it.
We can add and subtract without decrypting now, so what other operations can we do?
In theory, multiply and divide are just repeated add/subtract - but sadly this doesn't work in practice in our crappy cryptosystem.
To see why, let's look at a simpler version of our cryptosystem - it deals only in single numbers, the plaintext is p, the key is k and the ciphertext is c, no giggling please:
k = 9
p = 60
c = 69+9 = 69
Now let's do a homomorphic transform and multiply 69 by 2 yielding 138. 60 multiplied by 2 is 120, so if this works we should expect that 138-9 = 120
Sadly, 138-9 is in fact 129.
If we multiply the key by 2 as well we get this:
k = k2 = 18
c = 692 = 138
p = c-k = 138-18 = 120
Let's try this with multiplying by 3:
p3 = 603 = 180
k = k3 = 27
c = 693 = 207
p = c-k = 207-27
Put simply, it appears we can multiply the encrypted ciphertext and then decrypt it just fine - so long as we know in advance that it was in fact encrypted and what the operation was.
Of course the problem here is since we need to communicate what we multiplied it by anyway, it's pretty pointless to pass along the modified c variable - we can just pass along the fact we multiplied it by 3 and then it can be decrypted the normal way and multiplied by the receiver.
Let's look at what this has to do with AI now.
Introducing the magical homomorphic neural net
You should remember my previous article from earlier today about neural nets. If not, go find and read it and then come back here. I'll wait.
What would be really cool is running neural networks on encrypted data - that'd be cool, right?
We can model any sort of function (including the function "run this neural network") as a homomorphic operation if we can build a function with one property: whatever transformations performed on the function's input must be reflected in the decrypted form of that input when the input is encrypted.
For a simple neural network, the inputs are floating point numbers and the outputs are other floating point numbers. Because we need precision, we'll first scrap the floating point numbers and use integers.
We can of course scale our numbers easily enough - the exact scaling depends on application. Let's begin by building a sample network.
Last time we built a neural net and trained it on an AND function with 2 outputs (to represent 1 and 0). This time let's instead use 2 inputs and a single output.
To make it super simple, we'll use a single neuron in the hidden layer.
Here's one I ripped from google earlier:
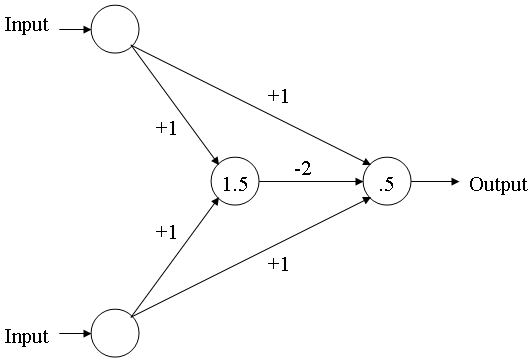
That one actually comes from the very cool page at http://mnemstudio.org/neural-networks-multilayer-perceptrons.htm and also seems the simplest possible XOR network around.
To run this neural net as a function is quite simple:
def run_net(input_vals):
hidden = sum(input_vals)
if hidden >= 1.5:
output = sum(input_vals)-2
else:
output = sum(input_vals)
if output >= 0.5:
output=1
else:
output=0
return output
print 1,1,run_net([1,1])
print 1,0,run_net([1,0])
print 0,1,run_net([0,1])
print 0,0,run_net([0,0])
If you run the above code you'll see it's a totally accurate XOR of the simplest possible form.
Now let's see what happens if we transform the inputs in various ways and then reverse the transformation on the output.
A simple transform is to just double the input and then half the output, let's try that. Go ahead, try it.
Double the 1s in each of the run_net invocations.
Not that simple is it? For the lazy, the output is all 0 unless you use floats - in which case the first is 0.5
Our basic problem is finding a way to transform the inputs while preserving the behaviour of the network and while allowing the transformation to be adjusted (so we can use a key to control it).
First, we've got to lose those branches - the last one is simple, we can just spit the output variable out without checking it and let the decrypter worry about comparing it to 0.5 - after doing so it turns out that the exact same results are generated anyway.
The top branch now needs to be eliminated, let's try simply doing sum(input_vals)-2 and then do some more fiddling to try and get this function nice and linear. For this whole thing to work, we want to represent the network as a single equation with no branches. We also want to get the outputs as nice unsigned integers.
Here's what I got after some fiddling:
def run_net(input_vals):
output = (sum(input_vals)-2)+sum(input_vals)
output = abs(output)
return output
print 1,1,run_net([1,1])
print 1,0,run_net([1,0])
print 0,1,run_net([0,1])
print 0,0,run_net([0,0])
This yields the following outputs:
1 1 2
1 0 0
0 1 0
0 0 2
If we can turn this into a homomorphic operation, then the decrypter can handle turning 0 into 1 and 2 into 0.
First some sane assumptions that will come in handy for larger networks: we know the structure in advance when designing our homomorphic operation so we can swap out sum() for hardcoded addition.
Next we transform the function into a chain of simpler homomorphic operations:
def run_net(input_vals):
output = 0
output += input_vals[0]
output += input_vals[1]
output -= 2
output += input_vals[0]
output += input_vals[1]
output = abs(output)
return output
print 1,1,run_net([1,1])
print 1,0,run_net([1,0])
print 0,1,run_net([0,1])
print 0,0,run_net([0,0])
Let's restructure it a bit more - since order of operations with add and subtract doesn't matter, we'll stick subtract at the end.
Since abs() is not a homomorphic operation we'll scrap it - the decrypter can do that bit.
We'll also swap the subtraction for another addition to end up with this beautiful chain of homomorphic operations:
def run_net(input_vals):
output = 0
output += input_vals[0]
output += input_vals[1]
output += input_vals[0]
output += input_vals[1]
output += -2
return output
print 1,1,run_net([1,1])
print 1,0,run_net([1,0])
print 0,1,run_net([0,1])
print 0,0,run_net([0,0])
Now let's encrypt our input values.
First, we generate a key stream that gives us 2 numbers (for the 2 inputs): for this example I just chose manually 29 and 15.
Next, each time the function references an input value, we add the relevant key to it.
Here's the modified code and the output, see if you can spot the cryptographic flaw and then i'll explain why it isn't one:
def run_net(input_vals):
output = 0
output += input_vals[0]+29
output += input_vals[1]+15
output += input_vals[0]+29
output += input_vals[1]+15
output += -2
return output
print 'Encrypted:'
print 1+29,1+15,run_net([1,1])
print 1+29,0+15,run_net([1,0])
print 0+29,1+15,run_net([0,1])
print 0+29,0+15,run_net([0,0])
print 'Decrypted:'
print 1,1,run_net([1,1]) - ((29+15)*2)
print 1,0,run_net([1,0]) - ((29+15)*2)
print 0,1,run_net([0,1]) - ((29+15)*2)
print 0,0,run_net([0,0]) - ((29+15)*2)
Encrypted:
30 16 90
30 15 88
29 16 88
29 15 86
Decrypted:
1 1 2
1 0 0
0 1 0
0 0 -2
Ok, so the cryptographic flaw that most people will point out is that it's obvious what the inputs are when we're looking at the encrypted list - even worse, the keys are revealed if the original plaintext was 0!
In practice, this isn't a problem for the simple reason that each set of inputs in a real-world application would use a fresh sequence from the keystream. When done right, there's no way to figure out what the original inputs or the key is when given simply the encrypted inputs and the encrypted output.
What this can be used for
With some work it should be feasible to transform any pretrained neural network into a chain of homomorphic operations like above, and what's more - it should be feasible to automatically generate such functions when given a particular network and knowing the boundaries on the inputs and outputs.
Using a decent keystream source (ask a cryptographer for advice here) the actual contents of the inputs are always going to be impossible to calculate, but the network itself can still return an output.
Essentially, this whole system allows for 1 party to train a model and then make predictions based on encrypted input from another party without decrypting it first.
If you can figure out how to do useful work using just multiplication then you can use a "real" cryptosystem such as unpadded RSA. You simply encrypt 2 numbers with the same keypair and then multiply the ciphertexts together - when decrypted you get the multiplication of the 2 plaintext numbers.
Academic work is ongoing in the area of homomorphic encryption in general, but for now there are a few very interesting properties for distributed AI on untrusted networks with untrusted peers.
You know, getting a collection of peers who can't be trusted to all agree on a conensus, similar to how cryptocurrencies agree on a consensus about who owns how much balance and which transactions are valid.
If someone manages to crack a homomorphic sigmoid function do let me know - and then the games shall begin.
Yours truly in madness, death, pain and tentacles,
Gareth Nelson