How The Radius Of The Center Of the Earth Was Determined
Hello Steemians! Do you know how the radius of the Earth was determined two thousand years ago? It is a very interesting question. Imagine how the scientists of the old era had such a great imagination and still surprise us in the 21st century. One of these characters was Eratosthenes was born in Cyrene in the year 276 a. C was a mathematician, astronomer and geographer. Around the year 255 a. C
The study was conducted between the city of Siena and Alexandria, where several reports and observations were determined.
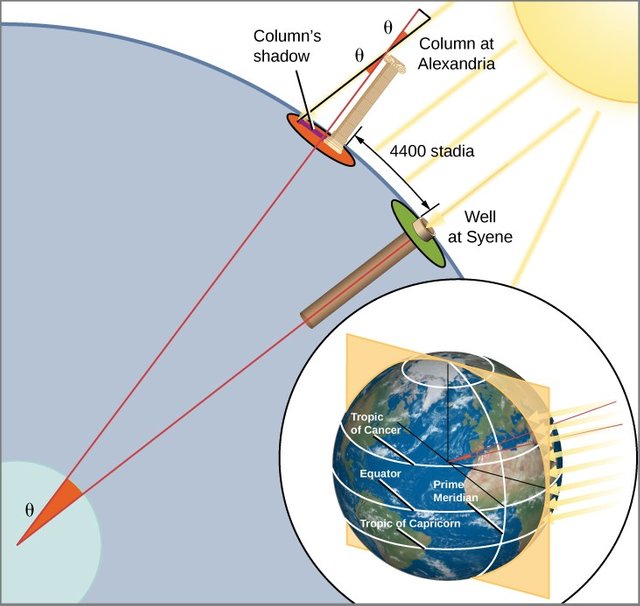
They began to generate hypothesis because at a certain time of the year on the summer solstice precisely (June 21) at noon, objects like (the obelisks) did not produce shade and at the bottom of the wells you could see the sunlight. Eratosthenes realized that, in Alexandria, the same day and at the same time, this same event did not happen.
"The summer solstice is the longest day of the year and is produced by the tilt of the earth's axis. In the summer solstice of the northern hemisphere, the sun reaches the zenith at noon over the Tropic of Cancer, that is, in the places located there, on June 21, the sun's rays fall vertically on the earth and, of course, how it is round, in the other places they fall inclined. The city of Siena is very close to the Tropic of Cancer line".
How the experiment was carried out To determine the radius of the earth
The track of Eratosthenes to measure the size of the circumference of the planet leads him to assume, in an acceptable manner, that the solar rays arrive parallel to the Earth due to their distance. Comparing the angles that these rays form and the verticals of each city with their prolongations to the center of the planet, they take it to a geometric configuration whose idea will be to measure the distance between two places that are on the same meridian, knowing the angular difference between they. And then compare that distance with the Earth's circumference. Finding your proportion.
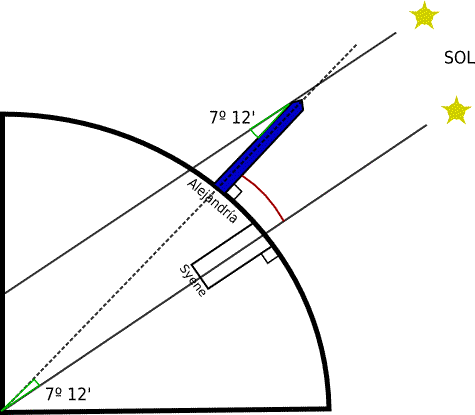
In this way he assures his idea that the surface of the Earth was curved because, had it been flat, this difference between the two cities would not have occurred.

Eratosthenes measures from Alexandria the height of the Sun (angle b) observing the shadow of a gnomon located in the center of a spherical solar clock called Scaphe, which has a marked lines where the angle of the projected shadow can be directly read. Meanwhile in Siena, the sun's rays illuminate the bottom of the well directly at noon, which indicates that it is directly above it. The difference between these two angles will have the same value as if we were taking the angle between the two cities measured from the center of the Earth.
The day of summer the sun is on the city of Siena, according to the scientist Eratosthenes thought, once the sun sets, the altitude of 90 degrees will be reflected in the sky, while in Alexandria, at that moment the instrument used called gnomon measures a height of the Sun above the horizon of 82.8 degrees (b). Then the angular difference between the two cities is 7.2 degrees (angle a in the graphs), which is the 50th part of a circumference. It only remains to know the distance between the two cities (d).
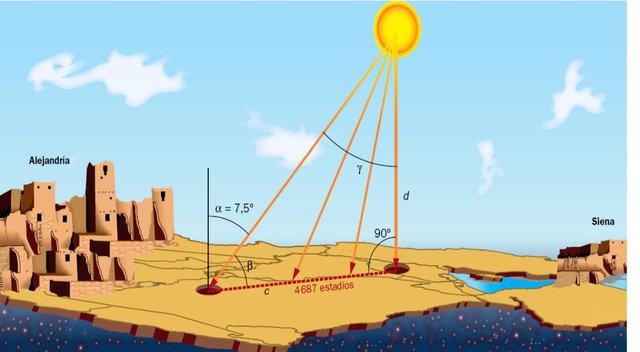
Source - Distance and angles used
Eratosthenes assumed the data of the commercial caravans that traveled between the cities, which took 50 days to 100 stages per day. A common stadium is equal to 157.2 meters, value given by the historian Pliny.
Eratosthenes when concluding all the data he needed, the story relates that he went to the library and began to calculate. Since the distance between the two cities is the arc of an angle equal to 1/50 of the circumference, it is obtained by multiplying that it measures 250,000 stadia. It is documented that Eratosthenes used the data of 252,000 stadiums since this number is easily divisible by 60, the number in which a circle was divided at the time. When we convert this value to meters and then to kilometers, we obtain the value of 39,614 km.


Reference:
- Erastostenes midio la circunferencia de la tierra - https://todaslascosasdeanthony.com/2012/07/02/como-eratostenes-midio-la-circunferencia-de-la-tierra-hace-2-mil-anos/
- Erastostenes y el centro de la tierra - https://circulosolar.wordpress.com/2011/10/10/un-gnomon-para-medir-el-planeta-i/
- El radio de la tierra - https://matesmates.wordpress.com/2011/01/13/eratostenes-y-el-radio-de-la-tierra/
