Hello friends of steemit, today continuing with my publications referring to the science of mathematics, I will talk about the derivative, their respective properties and also establish some examples, where the main derivation formulas are applied.

The derivative

In mathematics, the derivative of a function measures the speed with which the value of said mathematical function changes, as the value of its independent variable changes. The derivative of a function is a local concept, that is, it is calculated as the limit of the mean change rate of the function in a certain interval, when the interval considered for the independent variable becomes smaller and smaller. That is why we speak of the value of the derivative of a function at a given point.

A typical example appears when studying movement: if a function represents the position of an object with respect to time, its derivative is the velocity of that object. An airplane that makes a transatlantic flight of 4500 km between 12:00 and 18:00, travels at an average speed of 750 km / h. However, it may be traveling at higher or lower speeds in different sections of the route. In particular, if between 15:00 and 15:30 it covers 400 km, its average speed in that section is 800 km / h. To know its instantaneous speed at 15:20, for example, it is necessary to calculate the average speed in decreasing time intervals around this time: between 15:15 and 15:25, between 15:19 and 15:21

Then the value of the derivative of a function in a point can be interpreted geometrically, since it corresponds with the slope of the tangent line to the graph of the function in that point. The tangent line is in turn the graph of the best linear approximation of the function around said point. The notion of derivative can be generalized for the case of functions of more than one variable with the partial derivative and the differential.

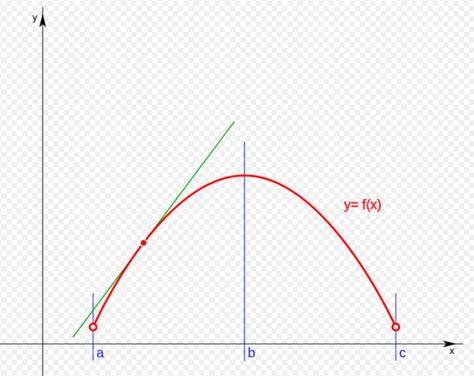
The derivative of the function at the marked point is equivalent to the slope of the tangent line (the graph of the function is drawn in red, the tangent to the curve is drawn in green).

Derivative definitions

In classical terminology, differentiation shows the coefficient in which a quantity changes as a result of a change in another quantity x.
In mathematics, coefficient is a multiplicative factor that belongs to a certain object such as a variable, a unit vector, a base function, etc.
In physics, coefficient is a numerical expression that by some formula determines the characteristics or properties of a body.
In our case, observing the graph on the right, the coefficient we talked about would be represented at the point P of the function by the result of the division represented by the relationship dy / dx, which, as can be seen in the graph, is a value that remains constant along the blue straight line that represents the tangent at the point P of the function. This is easy to understand since the right triangle formed in the graph with vertex at the point P, no matter how much we draw it bigger, being a proportional figure the result of dy / dx is always the same.
This notion constitutes the fastest approach to the derivative, since the approach to the slope of the tangent line is both on the right and on the left simultaneously.

Scheme showing the increments of the function in x and y.

Limit as difference quotient

The derivative of a function f is the geometric slope of the tangent line of the graph of f at x. Without the concept to be defined, it is not possible to directly find the slope of the tangent line to a given function, because only one point is known in the tangent line: (x, f (x)). The idea is to approximate the tangent line with multiple secant lines that have progressively smaller distances between the two intersecting points. When the limit of the slopes of the secant lines of this progression is taken, the slope of the tangent line is achieved. The derivative is defined, taking the limit of the slope of the secant lines, when approaching them to the tangent line. To find the slopes of the nearby secant lines, a relatively small number h is chosen. H represents a relatively small change in x, which can be positive or negative. The slope of the line that passes through the two point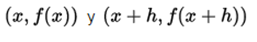s is :

expression called (Newton quotient).

The derivative of f in x is then the limit of the value of the differential quotient, as the secant lines approach the tangent line:

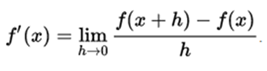
If the derivative of f exists at all points x, the derivative of f can be defined as the function whose value at each point x is the derivative of f at x. .
Since substituting h for 0 produces a division by zero, directly calculating the derivative may not be intuitive. One possible technique is to operate on the numerator, so that the denominator h can be canceled. And that is easily possible in polynomials. But for many other functions the result is uncertain. Fortunately, there are general rules that make it easy to differentiate most simple functions.

Secant line between f (x) and f (x + h)

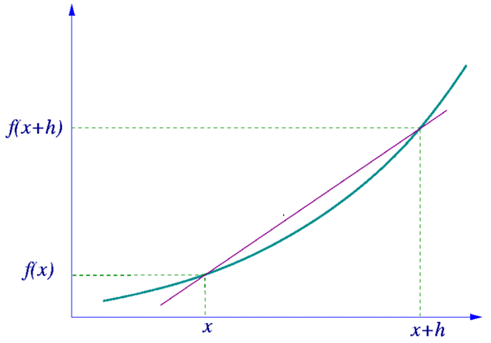
Inclinación de la secante de la curva y=f(x).

Derived from a function

Considering the function f defined in the open interval I and a fixed point a in I, we have that the derivative of the function f in the point a, is defined as follows:

if this limit exists, otherwise, f ', the derivative, is not defined. This last expression coincides with the instantaneous speed of the uniform continuous movement accelerated in kinematics.

Although all derivatives could be calculated using the definition of a derivative as a limit, there are well-established rules, known as theorems for calculating derivatives, which allow the derivative of many functions to be calculated according to their form without necessarily having to calculate the limit . Such rules are a direct consequence of the definition of derivative and previous rules, as can be seen in any good text of infinitesimal calculus.

Alternatively, the derivative of a function can be defined in any point of its domain in the following way:

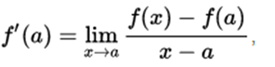
Which represents an approach of the slope of the secant to the slope of the tangent either on the right or on the left according to the sign of a. The aspect of this limit is related more to the instantaneous speed of the uniformly accelerated movement than to the slope of the line tangent to a curve.

Despite its apparent difference, the calculation of the derivative by definition with any of the limits previously expressed, always provides the same result.

Notation

There are several ways to name the derivative. Since f is a function, the derivative of the function f, with respect to the value x, is written in several modes.

Newton notation

Newton's notation for differentiation with respect to time, was to put a point above the name of the function:

and so on.

It reads «point x,» or «x, period». At the moment it is in disuse in pure Mathematics, nevertheless it continues being used in areas of the physics like the mechanics, where other notations of the derivative can be confused with the notation of relative speed. It is used to define the temporal derivative of a variable.

This notation of Newton is used mainly in mechanics, normally for derivatives that involve the variable time, as an independent variable; such as speed and acceleration, and in theory of ordinary differential equations. Usually it is only used for the first and second derivatives.

Leibniz notation

Another common notation for differentiation is due to Leibniz. For the function derived from f ,, we write:

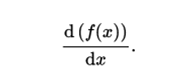
It can also be found as dy / dx, df / dx or d / dx f (x). It reads "derived from (f or f of x) with respect to x". This notation has the advantage of suggesting the derivative of one function with respect to another as a ratio of differentials.
With this notation, you can write the derivative of f at point a in two different ways:

If y = f (x), the derivative can be written as

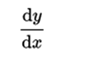
The successive derivatives are expressed as

for the nth derivative of f, or of and respectively. Historically, this comes from the fact that, for example, the third derivative is

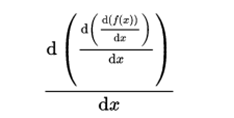
which can be written as

Leibniz's notation is very useful, since it allows to specify the differentiation variable (in the denominator); which is relevant in case of partial differentiation. It also makes it easy to remember the chain rule, because the terms "d" seem to be symbolically canceled:

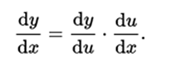
In the popular formulation of calculus by limits, the terms "d" can not be literally canceled, because they are indefinite by themselves; they are defined only when they are used together to express a derivative. In non-standard analysis, however, it can be seen as infinitesimal numbers that are canceled.

Certainly, Leibnitz (yes) considered the derivative dy / dx as the quotient of two "infinitesimals" dy and dx, called "differential". These infinitesimals were not numbers but smaller quantities than any positive number.

Lagrange notation

The simplest notation for differentiation, in current use, is due to Lagrange. To identify the derivatives of f, at point a, we write:
f (a) for the first derivative,
f "(a) for the second derivative,
f "" (a) for the third derivative,
f (a) for the nth derivative (n> 3). (Roman numerals can also be used).

It reads «f prime of x» for the first derivative, «f two bonus of x» for the second derivative, etc. For the function derived from f, in x, we write f¨ (x),. Similarly, for the second derivative of f, in x, we write f "(x) and so on.

THERE ARE SOME EXERCISES PRESENTED, WHERE THE BASIC PROPERTIES OF THE DERIVATIVE ARE APPLIED

References

1 . Serge Lang: "Introduction to mathematical analysis", p. 55
2 . Lee, Karel from: Calculus, Editorial University of Buenos Aires, p. 61, 1972
3 .Serge Lang: "Introduction to mathematical analysis" p.56

Bibliography

• Apostol, Tom M. (1967). Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra 1 (2nd edition). Wiley
• Spivak, Michael (1994). Calculus (3rd edition). Publish or Perish.
• Stewart, James (2002). Calculus (5th edition). Brooks Cole.