Probabilities: Elementary aspects
Hello to all friends of steemit readers
It is common knowledge that today, everything tends to be labeled from different perspectives, the analysis of all organic and inorganic objects, including natural phenomena as a whole, they are study objectives for their later disclosure and position within our intellectual system. One of the tools and perhaps the most important to understand these investigations are the numbers. The measurements and calculations applied by the scientific method specify the results that are used in all areas such as industry, biology, agriculture, technology, social and economic sciences, all these sectors are handled by means of numeric language.
The eagerness is such that you can even assign numbers to the possible events within the framework of sporting events, insurance, weather forecasts, trend in values of cryptocurrencies, electoral competition, financial market are the scenarios of the predictions that is quantified in terms of probabilities, this is just the point to be addressed, the fundamental aspects that statistical analyzes are used to calculate these values.
Elementary notions
The theory of probabilities originated in the seventeenth century, when some mathematicians among them Fermat and Pascal began to apply the laws of mathematics to the effects of chance, in simple terms the probability is the measure of the possibility of an event occurring, it implies the possibility that such an event does not occur. For example the case:
Image taken from a public domain source
What is the probability of choosing the ace of spades in a complete set of 40-card ?
The reasoning indicates that when choosing a card of the game there are two possibilities:
When choosing a card, the ace of spades appear
When choosing a card, the ace of spades does not appear.
Then the problem falls within the calculation of probabilities, since there is a possibility that the event occurs or not, in effect each letter has equal probability of appearing. The phrases equally possible, applied to future events that may or may not occur through a series of procedures, means that they are related in such a way that there is no reason to suppose that one of them has preference over the others.
Definition of mathematical probability
If an event can occur in m ways, everything is equally possible, and if within those m ways, n are favorable, the favorable probability p in the first trial is:
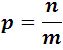
And the unfavorable q is:
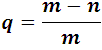
Thus, for example, the probability that a 6 will appear when a die is thrown is:
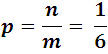
The probability that it does not appear by logic is 5/6, another example would be:
- Throw 2 dice and see what is the probability of adding on the first attempt 7 or 8?
Free use gif taken from Gifanimados
We know that each die can fall in 6 ways, and combining each of them with the six options of the other results in a total of 6x6 = 36, so that throwing the 2 dice is an event that can occur in 36 different ways and all equally possible. To add 7, we must count the favorable cases that are 1 and 6, 2 and 5, 3 and 4, 4 and 3, 5 and 2, 6 and 1, that is a total of six, therefore the probability of adding 7 is:
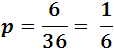
the same probability of rolling a die and taking 1 or 6 on the first try, for the case of 8 you can only get 2 and 6, 3 and 5, 4 and 4, 5 and 3, 6 and 2, is say, the favorable cases are 8 so the probability is of:
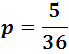
In general, the sum of the favorable and unfavorable probabilities is equal to 1. In effect:
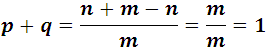
The favorable probability of an event is a number between ** 0 ** and ** 1 **. the unfavorable probability that an event occurs is equal to the unit minus the favorable probability, that is,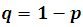 
, Similarly, if p is the favorable probability in a trial, the probability in k trials is kp , so for example, the probability of a 6 appearing when it is released a dice three times is 3/6, in 4 times it is 4/6, etc. In 6 trials, it would be 1, although it may not be possible, this is a very interesting point, that to explain properly it is necessary to deepen the theory of probability, in simple words it means that favorable events are much, but much more Probably the unfavorable, therefore it is almost impossible for an opposite event to occur, or what is the same as the most probable event is almost certain to occur.
Application of combinatorics to the calculation of probabilities
There are cases in which to list all the possible events and all the favorable cases are not as obvious as the previous examples, it is more frequent to see problems where the enumeration is tiring and it is convenient then to have certain formulas that allow to solve the problems with greater ease.
For example: What is the probability of taking 4 white cards out of a box containing 10 white, 4 black and 3 red?
As you can see, the number of ways you can choose 4 white cards among the 10 of that color is equal to the number of combinations of 10 objects taken from 4 in 4, that is, it is a C 10,4 while the total number of ways in which 4 cards can be chosen from 10 + 4 + 7 = 17 which contains the box C 17,4; therefore, the requested probability is:
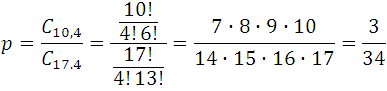
Obviously it is much smaller than taking a 6 by throwing a die.
Composite probability
When two or more events occur related to each other, it is called a composite event. They are events where the actions in a first attempt can alter or not other trials, that is, if we want to take out of a box that contains 5 white and 8 black cards, the amount of 6 cards What is the probability of taking 3 cards white and 3 black cards later?.
It is evident that the probabilities vary as cards are taken out, unless the cards are returned after the first attempt, starting from this case we can classify the events in:
- Independent events: are events whose production of each of them is not influenced by the production of the others.
Image taken from Pxhere (CCO)
- Dependent events: events that occur when affecting others.
Gif taken from Wikimedia (CCO)
In this way you can enunciate 2 very important properties:
- If the production probabilities of a group of n events are p1, p2, p3, ..., pn the probability that the whole event group will occur is
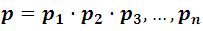
If we simultaneously throw a dice and a coin the probability that the face of the coin and the ace of the dice appear, it must be the multiplication of both probability, that is:
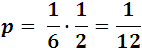
- If p1 is the probability that an event will occur and, after it occurs, the probability of a second event is p2, the probability of it happening both successively is p = p1. p2
Successively draw 2 aces in a deck of 40 cards, has a probability of 4/40 on the first attempt, and 3/39 for the second attempt, so the total probability would be.
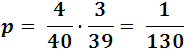
an event that is unlikely to occur.
Finally we have another event called
- Events that are mutually exclusive
It occurs when the production of one of them prevents the production of the others.
Image taken from Pxhere (CCO)
The total probability that one or the other of two mutually exclusive or reciprocally mutually exclusive events occurs is equal to the sum of the probabilities that events will occur separately.
- For example, suppose we have a wallet with coins of 20$ and 3 of 10$, another wallet with 2 of 20$ and 4 of 10$ coins, and a third with 3 coins of 20 $ and one of 10$. What is the probability of taking a 20$ coins from one of the portfolios chosen at random?
First it is clear that each portfolio has the same probability of being chosen, then if we choose the first one, its individual probability would be:
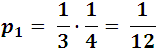
Analogously for the other 2, it would be:
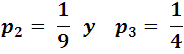
The total probability is then:
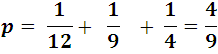
A value with almost 50% of occurring.
These are the fundamental aspects of the theory of probabilities, the beginning of more complete statistical methods that become more complex with the evaluation of new variables and other factors that are much more assimilated to the processes of our daily life, the fact is that almost nothing escapes the numbers or even the way to predict the future.
Bibliography referring to the text:
https://www.hiru.eus/es/matematicas/probabilidad-condicionada-y-compuesta
http://probabilidadmitad1.blogspot.com/p/eventos-dependientes-e-independientes.html
by @juancmz