Special relativity part 1: How Mr. Minkowski's theory of space time was integrated
Hello friends of Steemit, today I come to talk about special reltivity. It is too big and important a topic and a single publication would not cover all the information I want to provide. Today's topic is about What is four-dimensional space? What is the space-time interval? of the space-time theory of Hermann Minkowski.
THE TIME-SPACE OF MINKOWSKI
This structure was adopted by Einstein in his study of the movement of bodies in gravitational fields, which he describes in his general theory of relativity.
The theory of special relativity was endowed in 1907 with a geometric structure by Hermann Minkowski, which unified the concepts of space and time in a single four-dimensional reality, space-time, giving the same mathematical treatment to the three spatial coordinates that the temporal dimension (which in classical mechanics were considered independent and separate).
In classical physics, time is independent of the position and state of motion of the reference system. However, relativity establishes a four-dimensional continuum in which each point, called event or event, is described by three spatial coordinates and one temporal coordinate.
Hermann Minkowski
Minkowski was born in Aleksotas, Russia (now Kaunas, Lithuania), and studied in Germany at the universities of Berlin and Königsberg, where he completed his doctorate in 1885. During his studies at Königsberg in 1883 he received the mathematics award from the Academy of French Science for a work on quadratic forms. Minkowski taught at the universities of Bonn, Göttingen, Königsberg and Zurich. In Zurich he was one of Einstein's teachers.
Minkowski explored the arithmetic of quadratic forms on n variables. His research in this field led him to consider the geometric properties of n-dimensional spaces. In 1896 he presented his geometry of numbers, a geometric method to solve problems in number theory.
Mathematical calculation according to Hermman Minkowski
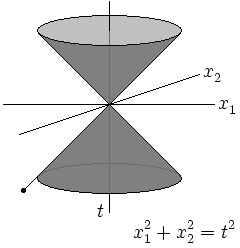
The Minkowksi space is a four-dimensional vector space similar to R4 whose elements or points are called events and have the form x μ = (ct, ~ x). The four-dimensional vectors that are defined in these spaces they are generically called quadrivectors. The space-time interval between two Minkowski space events (~ x1, t1) and (~ x2, t) is defined as the quantity
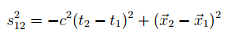
which responds to something as well as the equivalent of the Euclidean distance between two points. It is of vital importance the introduction of a metric that allows solve the problems related to space-time distances. The line element between two infinitesimally close events takes the form
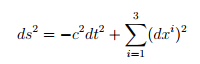
and it constitutes an invariant under the Lorentz transformations since, as we saw, we have built them precisely so that they leave invariant spatiotemporal interval between any two events. The metric (a (0, 2) - regular symmetric tensioner) can then be considered as η = diag (-1, 1, 1, 1). Observe that the choice of the signature1 (- +++) it is arbitrary since one of the type (+ - -) could have been taken. The introduction of this object allows the calculation of quadrivector standards and establish an isomorphism between covariant and contravariant indices in the space of Minkowski (which turns out to be a four-dimensional differentiable variety) so that the up and down operations make sense 'Indices as follows

where ημν are the components of the inverse of the metric tensor, which matches with the elements of the metric itself. The scalar product of quadrivectors is then
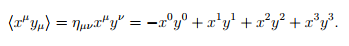
An especially important fact is that in a space of this form(It can be said that the symbol (- + ++) of the metric gives it the qualifier of pseudoriemanniana) it is possible to have zero non-zero vectors, and even vectors of negative norm without that for that reason we should be alarmed
Information reference
- Luis J.Garay, "Notes of Classical Electrophysics".
- I.E. Irodov, "Fundamental Laws of Mechanics", Mir.
- A.P. French, "Special Relativity", Revert'e.
- Ref 1
- Ref 2
- Ref 3
Thank you for taking the time to read this publication. I hope you have a happy day, see you in the next. Do not forget to leave a comment about what you thought, thank you very much. @juanjdiaz89


This post has received gratitude of 0.25 % from @appreciator thanks to: @juanjdiaz89.