Numerical Method in C++ Programming | Secant method (Method of Iteration) implemented in C++ Programming using Code::Blocks

What is Secant Method?

The Secant Method is a root-finding algorithm that uses two initial approximations to start the iteration process. This root-finding algorithm uses a succession of roots of secant lines to better approximate a root of a function f(x) from to intial approximation x0 and x1.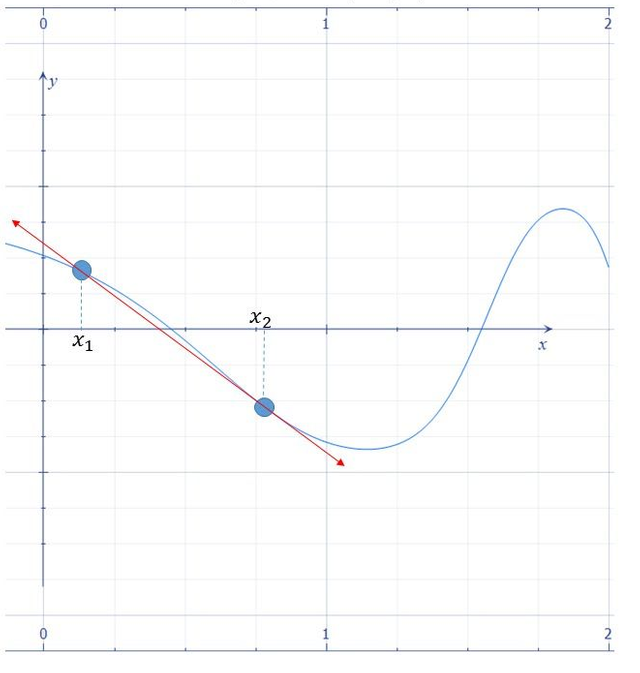

Intended Learning Outcome (What I will Learn?)

---

The readers should be able to:

1. learn how to do solve the roots of a function f(x) by using Secant method;
2. write a code to implement the Secant method algorithm in C++ programming language; and,
3. run the code written in C++ for Secant method algorithm using Code::Blocks.

Requirements

---

To be able to follow this tutorial, you need to have the following tools:

• A desktop PC or laptop with Windows (7, 8, 10) operating system; and,
• An installed GCC Compiler and Code:: Blocks Open Source cross-platform IDE software.

If you do not have the following software, you can download the Code:: Blocks software from codeblocks.org. For the GCC Compiler, you can download a MinGW compiler from mingw.org.

Furthermore, it is advisable that you must read the other curriculum for the Numerical Method using C++ Programming. The links can be found on the curriculum section in this tutorial.

Difficulty

---

• Advanced

Secant method of iteration implemented in C++ Programming using Code::Blocks

Part 1: Setting up and writing the code for Newton-Raphson Algorithm

---

Setting up a New Project in Code::Blocks
Use the console application template in Code::Blocks to start a new project. Set in C++ as the programming language to be used. For the detailed instruction, feel free to read the the first part of Numerical Method using C++ Programming #1 For this tutorial, save the project as Secant Method. Then, go to Secant Method> Sources > main.cpp

---

Setting up function Secant() which contains the the Secant Method algorithm

---

1 | As usual, start the program by declaring and defining standard libraries to be used. Hence we are doing a numerical algorithm, include mathematical standard library <cmath>, and <iomanip> for number precision. Write the proper syntax as follows:

#include <iostream> #include <cmath> #include <iosmanip> using namespace std;

2 | Declare the function for Secant(). Choose an appropriate data type and use the syntax data_type function( data_type identifier); . Use a double data type for its flexibility to store characters, integers, and floating point as compared with integer and float data types. So, write your code according to the syntax structure. We will use three identifiers x, x0, and x1 for this tutorial. This identifiers will stroe the values of the root, and two values for our initial approximation.

double Secant(double x, double x0, double x1)

3 | Define the function Secant() with the Secant method algorithm. Use this syntax to do so: double Secant(double x, double x0, double x1){ "Secant_Method_Algorithm" } .

4 | Using a WHILE loop to translate and perform the Secant Method algorithm as indicated by the formula below.

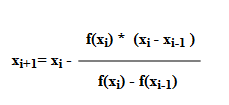
Set WHILE loop condition that will satisfy both scenarios:

Scenario	Syntax used
1. Absolute vale of f(x1) should begreater than as compared to the error	fabs(data_type, indentifier)> e
2. n approximations should be less than or equal to maximum iteration (Max_Iter)	n > = Max_Iter

You have take note that you should properly define n approximation, error e and maximum iteration Max_iter. You need to set values for n, e, and Max_Iter as "2", "0.0001", and "100" respectively. However, you may change the values for e and Max_iter base on your discretion.

double Secant(double x, double x0, double x1){ int n =2; const int Max_Iter=100; const double e=0.0001;

Write the WHILE loop condition inside the bracket . Incorporate the scenarios mentioned earlier using the "&&" (AND) operator.

while( (fabs(double x1) > e) && ( n <= Max_Iter)

5 | Define fx1 and fx0. For this tutorial, let have equation x^4 + x^2 = 0. So, use the syntax to pow(identifier, exponent) to get the result of raising the number to a certain exponent. This is the syntaxdouble fx0 = pow(x0,4) + pow(x,2);anddouble fx0 = pow(x0,4) + pow(x,2);```, after identifier is being replaced.

6 | Solve value of x using the formula as shown in step 4 . Writing down the formula as x=x1 - (fx1 * (x1 - x0)) / (fx1 - fx0);.

7 | Update values of x0 and x1. Use "=" operator change values stored at x0 and x1 to x1 and x respectively.

8 | To complete, the While loop operation, put a iteration counter so that the loop will terminate at n = Max_Iter. Do it by adding "++" operator besides n.

9 | Write down the complete code as describe in steps 4 to 8 in code::blocks.

double Secant(double x, double x0, double x1){ int n =2; const int Max_Iter=100; const double e=0.001; while( (fabs(double x1) > e) && ( n <= Max_Iter)){ double fx0 = pow(x0,4) + pow(x,2); double fx0 = pow(x0,4) + pow(x,2); x=x1 - (fx1 * (x1 - x0)) / (fx1 - fx0); x0=x1; x1=x; n++; } return n; }

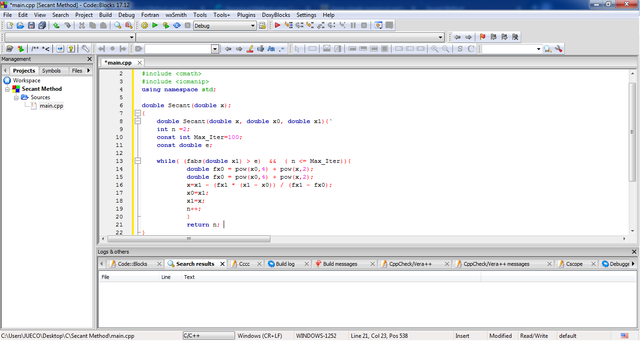
####Setting up I/O interface for the C++ program implementation of Secant Method (Method of Iteration )

---

10 | Inside the main() function, write a code that will allow user to input initial values for iteration. As usual, use cout<<"Text to be print " <<endl; and ```cin>>"identifier/placeholder" for output and input syntax respectively.

int main(double x, double x0, double x1){ cout << "Secant Method" << endl; cout <<"Enter first initial approximation: "; cin >>x0; cout <<"Enter second initial approximation: " cin >>x1; cout <<"\n The root of the equation is "<<x <<endl; return 0; }

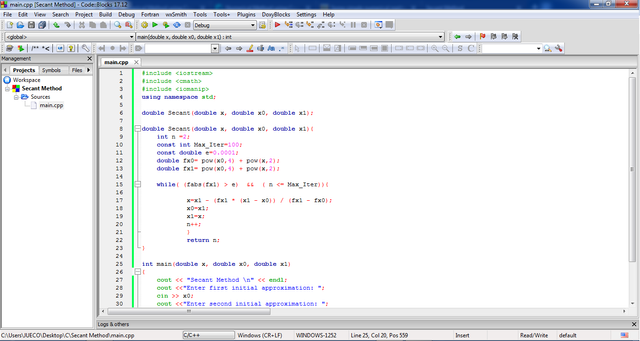
11 | Build the program by clicking .

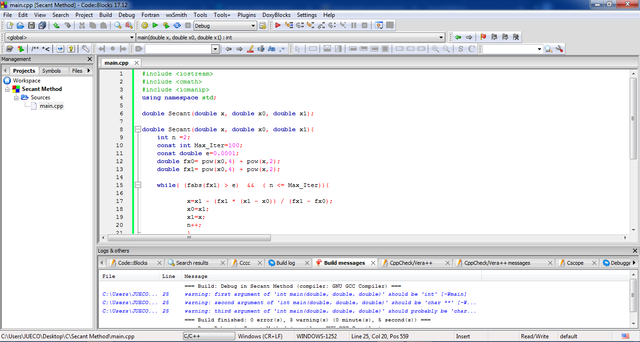
12 | Run the program by clicking .

Here is the complete code of the program we have done.

#include <iostream> #include <cmath> #include <iosmanip> using namespace std; double Secant(double x, double x0, double x1){ int n =2; const int Max_Iter=100; const double e=0.001; while( (fabs(double x1) > e) && ( n <= Max_Iter)){ double fx0 = pow(x0,4) + pow(x,2); double fx0 = pow(x0,4) + pow(x,2); x=x1 - (fx1 * (x1 - x0)) / (fx1 - fx0); x0=x1; x1=x; n++; } return n; } int main(double x, double x0, double x1){ cout << "Secant Method" << endl; cout <<"Enter first initial approximation: "; cin >>x0; cout <<"Enter second initial approximation: " cin >>x1; cout <<"\n The root of the equation is "<<x <<endl; return 0; }

PART 2: Running the output program

---

1 | Input a guess root. For example, i entered first and second initial approximation as 4 and 5 respectively.

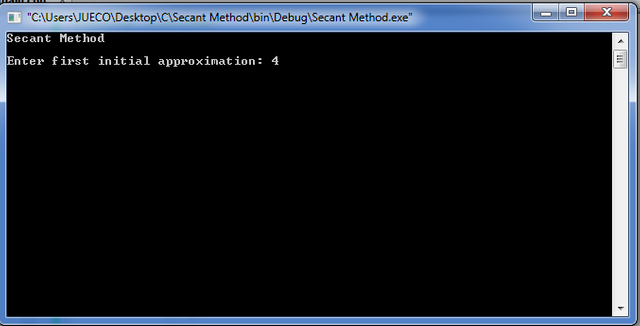
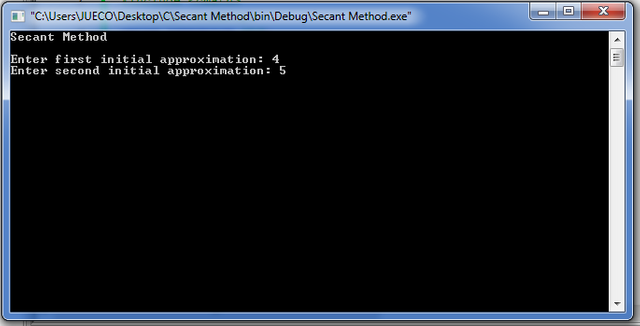
2 | Press ENTER to show result.

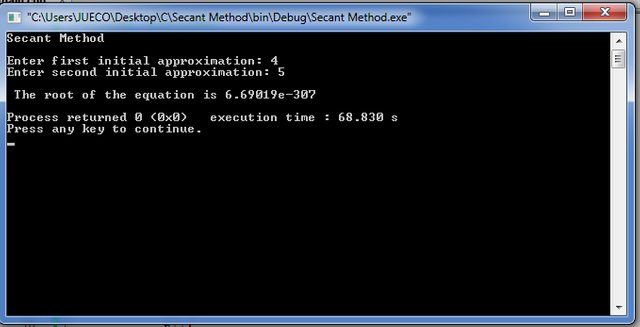
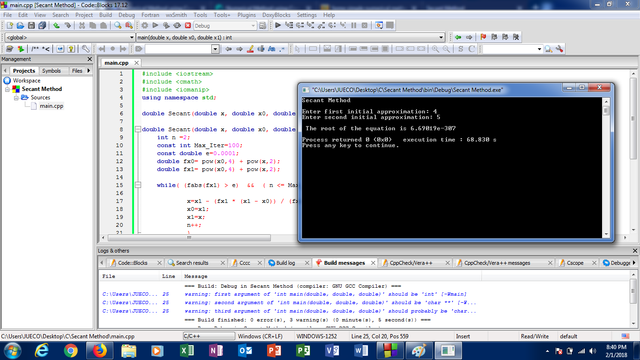
Curriculum

---

Here is the other tutorial for Numerical Methods on C++ series:

• (1) Numerical Method in C++ | Gaussian Elimination implemented in C++ programming using Code:: Blocks

• (2) Numerical Method using C++ programming | Newton-Raphson method of finding roots implemented in C++ programming using Code::Blocks

---

Posted on Utopian.io - Rewarding Open Source Contributors

---