Why Do I Sometimes Get Better Accuracy With A Higher Learning Rate Gradient Descent?

Simple.

You’re overstepping local minima to converge on something closer to the global minimum.

Consider the following graph:

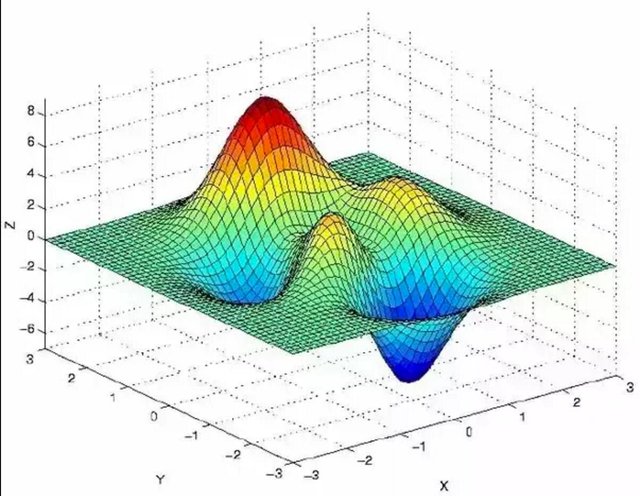
Although your model probably has more dimensions, let this graph represent the decisions space of a three dimensional model. (this is because humans generally suck at visualizing more than three dimensions, but the math doesn’t give a shit, so we are all good)

Imagine you are standing somewhere on the graph above. Let’s for the sake of demonstration say that your initial position is at the top of the red uprise around point (0,2,6).

Currently, your loss function value is super high (6) - this is what you want to minimize.

Take a moment to look at the graph. If we want to minimize our loss function (the z value), where would the optimal convergence point be?

The answer is somewhere around (0,-2,-6), so this is where we want our algorithm to end up.It’d be great if there’s a GOTO(global_minima) function, but there isn’t. In fact, we actually know is the function that produced this graph (the loss function) - the graph is just an educational tool.

Now, I won’t go too much into other optimization algorithms as this is primarily about gradient descent, but I’ll briefly mention that the naive approach of trying random values Monte Carlo style won’t be very efficient as you’re assuming there’s no relationship between good and bad values.

For the Monte Carlo method to be efficient, the graph should look something like this where the dots are points on the graph (with random values):

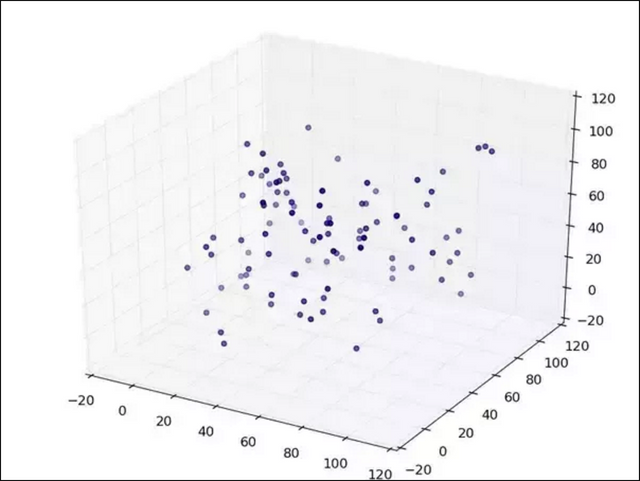
Gradient descent is a better alternative to our naive approach. Gradient descent works by taking a step towards a lower point on the graph, and continuing to do so until you reach somewhere where you can no longer take a step down. This is where the algorithm converges.

The length of each step is what we call the learning rate.

Let’s try to run this algorithm on our graph above.

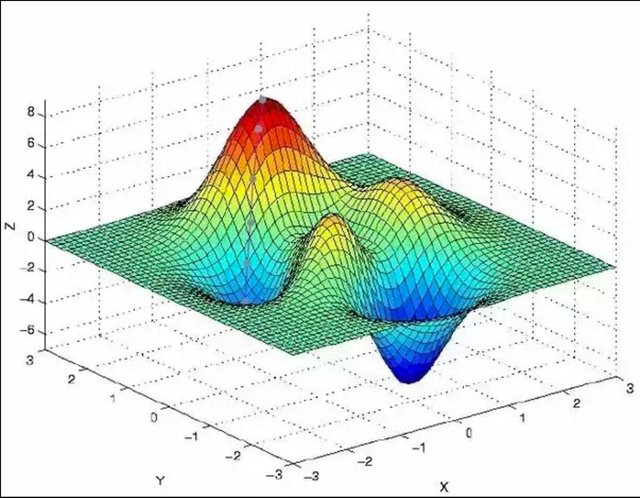
(I recognize that this was poorly drawn. The distance between the points is supposed to be constant)

We see that the algorithm converges in (-1,2,-4), and not (0,-2,-6) which we determined would be the optimal outcome.

To answer your question, the reason you see an improved accuracy when you increase the learning rate is that it oversteps some of the local minima, and therefore converges closer to the global minimum (not spatially necessarily, but in value).

Mathematically, gradient descent works by taking the derivative of each variable (each dimension) to determine which way it should step. If done numerically, this is the equivalent of feeling with your feet which way will make you go down the fastest, and updating the position based on the learning rate.

position = position + learning_rate * direction_vector

The algorithm can therefore be classified as greedy as it has no sense of the overall landscape, and is thus limited to making the logical choice at each position as it doesn’t have a concept of the overall landscape, and thus the global minima.

When using gradient descent, you’re only guaranteed to converge on a local minima; not the global minima. Though in practice, gradient descent rarely converges. Instead, it’s trained for n iterations, or until it doesn’t improve the accuracy anymore.

It’s possible to minimize the chance of converging on only a local minima by training the network multiple times using different initialization points; the point on the high dimensional graph from where you start your descension.

The problem with this technique is that it requires a lot of computing power, and doesn’t necessarily improve your results (there’s still no guarantee that it will find a better local minima).

Furthermore, by introducing an element of randomness, you give up the determinism which may be a problem in some scenarios.

Other ways of minimizing the odds of convergence on local minima include using the momentum method, and stochastic gradient descent. There are a few other as well, but they all fall into the category of optimizers.