TENSORS. BASIC CONCEPTS. PART 2
Hello friends of steemit, today I present the second part of the basic concepts of tensors.
TRANSFORMATIONS OF COORDINATES. GENERAL TENSORS
we will represent by (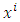 
) the arbitrary system of coordinates (
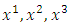) in a three-dimensional Euclidean space, and by 
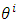any other coordinate system (
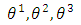) in the same space.
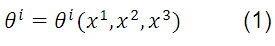
The equations of transformation of coordinates (1) assign to any point (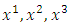) in the system 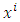, a new set of coordinates (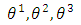) in the system 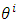. It is assumed that the functions 
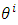that relate the two sets of variables are single value functions, continuous and differentiable.
The determinant is given by equation (2) which is called the Jacobian of the transformation
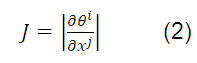
The coordinate systems represented by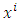 
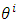and are completely general and can be any curvilinear or Cartesian system.
In equation (3), the differential vector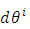 
is given by:
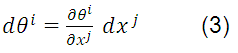
This equation is a prototype of the one that defines the class of tensors known as contravariant vectors. It is said, in general, that a set of quantities associated with a point P are the components of a contravariant tensor of order one if it is transformed under a coordinate transformation given by the following equation:
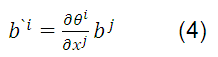
Here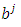 
are the components of the tensor in the coordinate system 
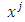, while 
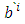are the components in the system 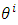. In the general theory of tensors, contravariant tensors are recognized by the use of written indices as superscripts.
On the other hand, covariant tensors are recognized by the use of subscripts. The covariant vector prototype is the partial derivative of a scalar function of the coordinates.
If Φ = Φ (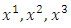
) is a function, you have to:
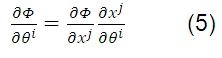
In general, a set of quantities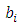 
are the components of a covariant tensor of order one if they are transformed according to the equation:
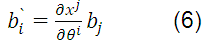
Where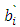 
are the covariant components in the system 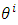and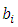 
the components in the system 
.
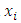The covariant tensors of the second order obey the law of transformation:
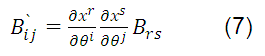
THE METRIC TENSORS. CARTESIAN TENSORS
We will represent by 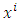a system of rectangular Cartesian coordinates in a three-dimensional Euclidean space, and by 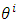, any system of curvilinear or rectangular coordinates, that is, cylindrical or spherical coordinates in the same space. The vector x that has the Cartesian components 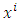is called the vector of the position of the arbitrary point P (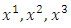) referred to rectangular Cartesian axes. The square of the differential element of the distance between two very close points P (x) and Q (x + dx) will be:
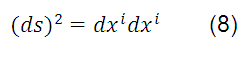
Of the coordinate transformation that relates the systems, the differential distance is:
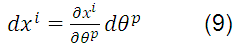
then, equation (8) becomes:
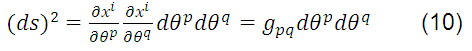
where the second order tensor:
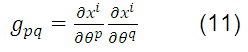
it is called the metric tensor or fundamental space tensor.
Any coordinate system for which the differential element of distance squared takes the form of equation (8), is called a system of homogeneous coordinates.
The coordinate transformations between homogeneous systems are orthogonal transformations, and when we consider these transformations, the tensors thus defined are called Cartesian tensors.
For the Cartesian tensor there is no distinction between the covariant and contravariant components and therefore only subscripts are used in the expressions that represent the Cartesian tensors.
MATRIX REPRESENTATION OF CARTESIAN TENSORS
A grouping of elements contained between two large brackets and that depend on certain laws of transformation, is called a matrix.
A matrix M x N is the one that has M rows and N columns of elements. In the symbol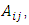 
used to represent a typical element of the matrix, the first subscript indicates the row and the second indicates the column occupied by the element.
A square A matrix (M = N) can be represented by:
A 1 x N matrix is called a row matrix. An M x 1 matrix is called a column matrix. A matrix that only has zeros as elements is called a null matrix. A square matrix with all its null elements except those of its main diagonal (from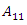 
to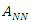 
) is called a diagonal matrix. If the nonzero elements of a diagonal matrix are all the unit, the matrix is called the identity matrix. The matrix N x M, formed by changing the rows by columns of the matrix M x N is called the transposed matrix 
.
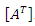REFERENCES
Mase, G., 1977, Mecánica Del Medio Continuo, Libros McGraw Hill de México, S.A. de C.V.
Borisenko, A.I. y Tarapov, I. E., 1968, Vector and Tensor Analysis with Applications, Dover Publications, Inc. New York, USA.
Goicolea, J., 2002, Mecánica De Medios Continuos: Resumen de Álgebra y Cálculo Tensorial, Universidad Politécnica de Madrid, España.
Sokolnikoff, I. S., 1951, Tensor Analysis: Theory and Applications, Jhon Wiley & Sons, Inc. New York.
Murray R., Seymour, L. y Dennis, S., 1998, Análisis Vectorial, 2° edición, McGraw-Hill/Interamericana editores, S.A. de C.V.