TENSORS. BASIC CONCEPTS. PART 3
Hello friends of Steemit, today I present the third part of the basic concepts of tensors.
FUNDAMENTAL OPERATIONS WITH TENSORS
Addition and subtraction of tensors:
The sum or difference of two or more tensors of the same order and type, that is, the same number of contravariant indices and the same number of covariant indices, results in a tensor of the same order and type.
If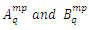 
are tensors, then
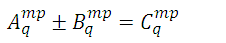
The addition of tensors is commutative and associative.
Multiplication of tensors
External product
the product of two tensioners is a tensioner whose range is the sum of the ranges of the given tensors. This product, which involves the ordinary multiplication of the tensor components, is called the external product.
If you have the tensors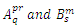 
, the external product of these two tensors is the following:
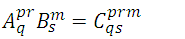
Not every tensor can be written as the product of two tensors of lower rank, for this reason the division of tensors is not always possible.
Contraction
if a contravariant index and a covariant index of a tensor are matched, the result indicates that a summation must be taken on the equal indices according to the summation agreement. This resulting sum is a tensor that has an order twice less than the original.
For example, in the tensor of order 5,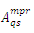 
is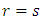 
to obtain:
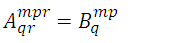
which is a tensor of order 3. Also, if we do p = q we get
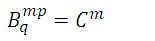
which is a tensor of order 1.
Internal product
by the process of the external product of two tensors followed by a contraction, a new tensor called internal product of the given tensors is obtained. The process is called internal multiplication.
For example, given the tensors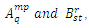 
, the external product is 
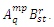. By doing q = r we obtain the internal product 
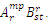. When q = r and p = s, another product 
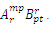is obtained.
The internal and external multiplication of tensors is commutative and associative.
SYMMETRY OF MATRICES AND TENSORS
Since the interchange of indices of a second-order tensor is equivalent to the exchange of rows by columns in their matrix representation, a square matrix A will be symmetric if it is equal to its transpose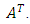 
. So, a 3x3 symmetric matrix has only six independent components, as follows:
An anti-symmetric matrix is equal to the negative of its transpose. An anti-symmetric matrix B 3x3, has zeros in its main diagonal, and therefore, has only three independent components.
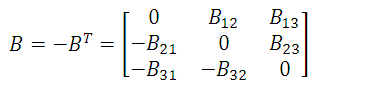
The properties of symmetry can be extended to tensors of an order greater than two. In general, it is said that an arbitrary tensor is symmetric with respect to a pair of indices, if the value of the typical component remains invariable when exchanging these two indices. A tensor is anti-symmetric with respect to a pair of indexes if the exchange of these leads to a change of signs without a change in the absolute value of the component.
Below are some examples of the properties of symmetry in higher order tensors:
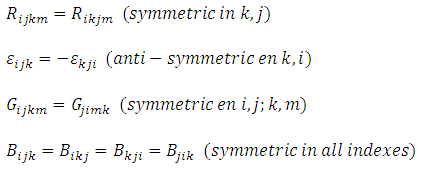
TENSORIAL FIELDS
If a defined tensor corresponds to each point of a region in a N-dimensional space, we say that a tensor field has been defined. This is a vector field or a scalar field, depending on whether the tensor is of rank one or zero, it should be noted that a tensor or tensor field is not only the set of its components in a special coordinate system, but all possible sets with any coordinate transformation.
A tensor field associates a tensor T (x, t) to each pair (x, t), where the position vector x varies in a particular region of space and t varies in a particular time interval. It is said that a tensor field is continuous (or differentiable) if the components T (x, t) are continuous or differentiable from x and t. if the components are functions of x only, the tensor field is said to be stationary.
Regarding a system of rectangular Cartesian coordinates, where the position vector of an arbitrary point is:
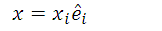
The tensor fields of several orders are represented by:
scalar field: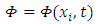 
vector field: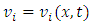 
Second order tensorial field: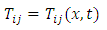 
REFERENCES:
Mase, G., 1977, Mecánica Del Medio Continuo, Libros McGraw Hill de México, S.A. de C.V.
Borisenko, A.I. y Tarapov, I. E., 1968, Vector and Tensor Analysis with Applications, Dover Publications, Inc. New York, USA.
Goicolea, J., 2002, Mecánica De Medios Continuos: Resumen de Álgebra y Cálculo Tensorial, Universidad Politécnica de Madrid, España.
Sokolnikoff, I. S., 1951, Tensor Analysis: Theory and Applications, Jhon Wiley & Sons, Inc. New York.
Murray R., Seymour, L. y Dennis, S., 1998, Análisis Vectorial, 2° edición, McGraw-Hill/Interamericana editores, S.A. de C.V.