How Likely Are Coincidences?
Napoleon and Hitler, were born 129 years apart, they also came into power 129 years apart, and they both declared war on Russia 129 years apart. What’s even more unbelievable is that they were both defeated 129 years apart. What does this all mean? Is this just a coincidence or is there some big conspiracy behind all of this? Why is it so easy to find a relationship between two events that are independent? If you do a little bit research on the internet you’ll find a bunch of spooky, and historical coincidences that almost seems too good to be true.
Formally defining a coincidence; according to dictonary.com a coincidence is “a striking occurrence of two or more events at one time apparently by mere chance”. Under these circumstances the situation above involving Napoleon and Hitler was a pure coincidence… right? You see, that’s thing about coincidences, they almost seem too good to be true. So much so, that we sometimes assume a greater power may be at work but when you sit down and really analyze: “how likely are coincidences?” you may be surprised to learn that they aren’t as unlikely as we may believe.

Let’s analyze coincidences with a little bit of math and start with the basics: we know that probability is used described the likelihood of some event to occur, for example; the probability that you will get heads from a fair coin toss is 0.5, because there are only 2 sides to a coin; heads and tails resulting in ½ chance of receiving heads. Therefore, if I told you (the reader) to toss a coin and while I toss a coin what is the chances that you and I would both get heads?

Well, you have a probability of 0.5 to get heads, and I have a probability of 0.5 to get heads. Both events are independent of each other; therefore, we multiply our probabilities and get a probability of 0.25 of both obtaining heads. In other words, we have a 25% chance getting heads together, at this very moment, which is surprisingly higher than what most people would assume.
Now imagine if you and I engaged in this activity right now, and we both get heads. If I hadn’t explained the math behind our chances, our results may appear as a spooky coincidence; as I am nowhere near you to influence your chances of getting heads. Which is actually a false statement because it would not matter if I were next to you, or on another planet during a fair coin toss.
My presence does not affect the probability of achieving heads from a fair coin toss because the coin toss is an independent event. This means that you will always have the same probability (0.5) of getting either a head or tail from a fair coin toss. This is a common misconception in understanding independent events. If an event is truly independent then other external factors cannot affect the probability of that event occurring.

Another interesting turn of events in probability theory is the birthday problem. The birthday problem or the birthday paradox states that in a set of ‘n’ randomly chosen people some pair of them will have the same birthday. This should make sense because if we have a total of 366 possible birthdays (including the 29th of February) and we have 366 people, we will defiantly see a pair of individuals who share the same birthday.
However, what makes the birthday problem famous is that; with only 70 people there is a 99.9% chance that 2 out of the 70 people in that group will share the same birthday. If we go even further; we can statistically prove that in a group of 23 individuals, we will have a 50% chance that 2 out of the 23 individuals will share the same birthday. Can someone say “illuminati confirmed”?
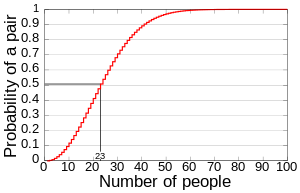
The birthday problem is arguably the best mathematical model suited to explain the chances of coincidences. Considering that a birthday occurs only 1 out of 366 days. In small group of 23 individuals, we’re somehow able to get a 50% chance that 2 individuals will share the same birthday. We can prove this mathematically using a suite of statistical tools (combinations, permutations, etc.), which means according to probability it should come as no surprised that coincidences aren’t as unlikely as you may think!
TL;DR (Abstract): A coincidence is “a striking occurrence of two or more events at one time apparently by mere chance”. Surprisingly, there is plenty of historical and spooky coincidences you can find doing a little bit research on the web. For example; Napoleon and Hitler, were born, put into power, declared war on Russia and we're defeated all at 129 years apart.
That’s the thing about coincidences; we sometimes assume that there is a relationship between some independent event A and some independent event B because the likelihood of those two events occurring seem highly unlikely. It’s almost as if the occurrences between these two events are too good to be true therefore we assume a higher power must be at work. However, it turns out that coincidences are more likely than we may think and there really isn’t any greater conspiracy at play.
If you don’t believe me, take a look at the famous probability theory problem: The Birthday Paradox. The birthday problem or the birthday paradox states that in a set of ‘n’ randomly chosen people some pair of them will have the same birthday. This should make sense because if we have a total of 366 possible birthdays (including the 29th of February) and we have 366 people, we will defiantly see a pair of individuals who share the same birthday. However, what makes the birthday problem famous is that; with only 70 people there is a 99.9% chance that 2 out of the 70 people in that group will share the same birthday. If we go even further; we can statistically prove that in a group of 23 individuals, we will have a 50% chance that 2 out of the 23 individuals will share the same birthday. Can someone say, “illuminati confirmed”?
The birthday problem is arguably the best mathematical model suited to visualize the occurrence of coincidences. Coincidences aren’t as unlikely as we thought, and next time something crazy happens, before jumping to some illogical conspiracies rest assured; that Earth is indeed not flat.
REFERENCES:
- https://www.erepublik.com/en/article/two-tyrant-hitler-and-napoleon-and-their-mystical-coincidence-in-numbers--2311713/1/20
- https://understandinguncertainty.org/node/62
- https://www.newscientist.com/article/mg22129601-000-no-coincidence-statistics-and-the-outrageously-unlikely/
- https://plus.maths.org/content/what-coincidence
- https://en.wikipedia.org/wiki/Birthday_problem
- https://en.wikipedia.org/wiki/Probability_theory
Note: A big thanks to @steemstem for providing fun and educational content relating to Science, Technology, Engineering and Math!

a very dancing story.
regards steemit let me follow and upvote
you
introduce my name @asteemit from indonesia thank you.
hope you continue to succeed
Congratulations @mindhacks! You have received a personal award!
Click on the badge to view your Board of Honor.
Congratulations @mindhacks! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!