Whitepaper do bitcoin em português
Whitepaper do Bitcoin por Satoshi Nakamoto
Abstract. Uma versão de dinheiro eletrônico puramente ponto-a-ponto permitiria que pagamentos online fossem enviados diretamente de uma pessoa para outra sem a necessidade de passar por uma instituição financeira, como bancos, por exemplo. Assinaturas digitais oferecem uma parte da solução, mas os principais benefícios são perdidos se um intermediário confiável ainda é necessário para prevenir o gasto duplo.
Nós propomos uma solução ao problema do gasto duplo utilizando uma rede ponto-a-ponto. A rede registra a data e hora das transações através de um sistema de carimbo de tempo, transformando-as em uma cadeia contínua de prova de trabalho baseada em um hash, formando um registro que não pode ser modificado sem que toda a prova de trabalho seja refeita.
A cadeia mais longa não serve apenas como uma prova da sequência dos eventos testemunhados, ela serve também como uma prova de que ela veio do grupo com maior poder computacional. Enquanto a maioria do poder computacional é controlada por nós de rede que não estão cooperando para atacar a rede, eles vão gerar a maior cadeia e ultrapassar os atacantes.
A própria rede requer uma mínima estrutura. As mensagens são transmitidas com o melhor esforço base e, os nós de rede podem sair e se juntar a rede quando quiserem, aceitando a cadeia com a prova de trabalho mais longa como uma prova do que aconteceu enquanto eles estiveram fora da rede.
Introdução
O comércio na internet passou a se tornar quase que exclusivamente dependente de instituições financeiras se propondo como terceiros confiáveis para processar pagamentos eletrônicos. Enquanto o sistema funciona bem o suficiente para a maioria das transações, ele ainda sofre de fraquezas inerentes em modelos baseados na confiança em terceiros ou intermediários. Transações completamente irreversíveis não são realmente possíveis, porque as instituições financeiras não podem evitar mediação de disputas judiciais. O custo das mediações aumenta os custos de transação, limitando o tamanho mínimo que uma transação deve possuir e acabando com a possibilidade de pequenas transações casuais, além disso, há um custo mais amplo na perda da possibilidade de fazer pagamentos irreversíveis para serviços irreversíveis.
Com a possibilidade de pagamentos reversíveis, a necessidade de confiança aumenta. Os comerciantes precisam estar atentos aos seus clientes, incomodando eles para darem mais informações do que eles precisam oferecer normalmente. Uma certa porcentagem de fraude é aceita como inevitável. Essas incertezas de custos e pagamentos podem ser evitados com uma pessoa usando uma moeda física, entretanto, não existe nenhum mecanismo para fazer pagamentos através de um canal de comunicações sem um terceiro.
O que se torna necessário é um sistema de pagamentos eletrônicos baseado em provas criptográficas ao invés de confiança, permitindo que duas partes dispostas a negociar diretamente entre si possam o fazer sem a necessidade de um terceiro confiável. Transações que são computacionalmente impraticáveis de serem revertidas protegem os vendedores de caírem em alguma fraude. Além disso, mecanismos de rotina de depósitos poderiam ser facilmente implementados para proteger os compradores.
Neste artigo nós propomos uma solução para o problema do gasto duplo usando um servidor ponta-a-ponta de carimbos de tempo para gerar uma prova computacional da ordem cronológica das transações. O sistema é seguro enquanto nós de rede honestos controlam coletivamente mais poder computacional do que qualquer outro grupo de nós de rede atacantes cooperando entre si.
Transações
Nós definimos uma moeda eletrônica como uma cadeia de assinaturas digitais. Cada proprietário transfere a moeda para a próxima pessoa, assinando digitalmente um hash da transação anterior e uma chave pública do próximo dono e adicionando a estes, a assinatura de sua chave privada que libera as moedas para a pessoa que vai recebê-las. A pessoa que recebeu a transação pode verificar as assinaturas para checar a cadeia de propriedade.
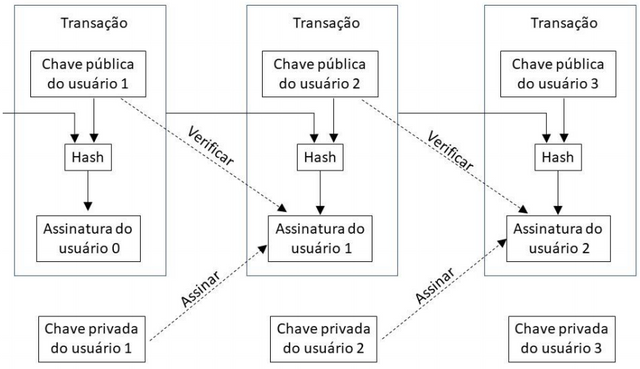
O problema, claro, é que quem recebe a moeda não pode verificar se um dos donos não gastou a mesma moeda duas vezes. Uma solução comum é introduzir uma autoridade central, ou uma “Casa da Moeda” que verifica se houve gasto duplo em cada transação.
Depois de cada transação, a moeda deve retornar à casa da moeda, que vai emitir novas moedas, e somente moedas emitidas diretamente pela Casa da Moeda são confiáveis de não terem sido gastas duas vezes. O problema dessa solução é que o destino de todo sistema monetário dependeria de uma instituição que estaria por trás da cunhagem das moedas, com cada transação tendo que passar por ela, como se fosse um banco.
Nós precisamos de um modo no qual quem recebeu a moeda saiba que os donos anteriores da moeda não assinou nenhuma outra transação prévia. Para nossos propósitos, a transação mais antiga é a que conta, então não nos importamos com tentativas mais recentes de gastos-duplo. O único modo de confirmar a ausência de uma transação é estar atento a todas as transações que ocorrem.
No modelo baseado em “Casas da moeda”, elas estavam atentas de todas as transações e decidiram qual delas foi feita primeiro. Para que isso seja feito sem um intermediário confiável, todas as transações precisam ser anunciadas publicamente [1], e nós precisamos de um sistema para que os participantes concordem em uma única ordem cronológica na qual todos eles receberam. Quem recebe as moedas precisa de uma prova para comprovar que naquele tempo, todos os nós de rede concordaram que aquela transação foi recebida primeiro.
Servidor de Carimbos de tempo
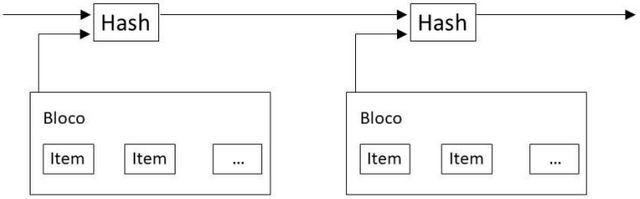
A solução que propomos começa com um servidor de carimbo de tempo. Um servidor de carimbos de tempo funciona pegando a função hash de um bloco de itens que serão carimbados com a data e a hora e publicando largamente a função hash, como se fosse um jornal ou um post na Usenet [2-5]. O Carimbo de tempo inclui o carimbo de tempo anterior em sua função hash, formando uma espécie de cadeia ou corrente, com cada carimbo de tempo adicional reforçando os anteriores.
Prova de trabalho
Para implementar um servidor de carimbos de tempo bem distribuído em uma base ponto-a-ponto, nós vamos precisar usar um sistema de prova-de-trabalho similar ao Hashcash de Adam Back [6], ao invés do jornal ou posts de Usenet. O sistema de prova-de-trabalho envolve escanear o valor que foi adicionado à função hash, como em um sistema de criptografia SHA-256, a função hash começa com um número de zero bits. O trabalho médio requerido é exponencial no número de zero bits requeridos e pode ser verificado executando um único hash.
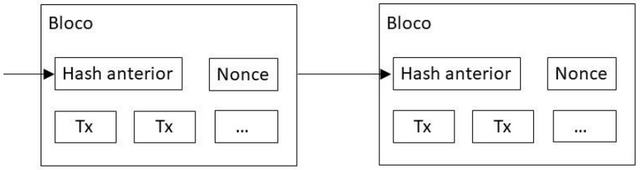
Para a nossa rede de carimbo de tempos, nós implementamos uma prova-de-trabalho através da incrementação de um nonce no bloco até que o valor seja encontrado e dê ao hash do bloco os zero bits requeridos. Como o esforço computacional foi gasto para satisfazer a prova-de-trabalho, o bloco não pode ser mudado sem que todo esse trabalho seja refeito. Conforme os últimos blocos são encadeados depois do primeiro, o trabalho para mudar o bloco incluiria refazer todo o trabalho gasto nos blocos depois dele.
A prova-de-trabalho também soluciona o problema de determinar a representação com uma maioria tomando as decisões. Se a maioria fosse baseada em um-ip-um-voto, ela poderia ser facilmente subvertida por qualquer um que pudesse alocar grandes quantidades de IPs. Prova-de-trabalho é essencialmente um-Computador-um-voto.
A decisão tomada pela maioria é representada pela maior cadeia de blocos, a qual contém a prova-de-trabalho com maior esforço investido. Se a maioria do poder computacional é controlada por nós-de-rede honestos, a cadeia honesta irá crescer mais rapidamente e ultrapassar qualquer cadeia de blocos competidora.
Para modificar um bloco anterior da rede, um atacante precisaria refazer toda a prova-de-trabalho do bloco atual e todos os blocos depois dele e, então recuperar o atraso e ultrapassar o trabalho de todos os nós-de-rede honestos. Mostraremos mais adiante que a probabilidade de um atacante mais lento ultrapassar os nós honestos diminui exponencialmente enquanto blocos subsequentes são adicionados.
Para compensar o aumento da velocidade dos hardwares e a variação do interesse em se rodar nós com o passar do tempo, a dificuldade da prova-de-trabalho é determinada por uma média móvel focando o número médio de blocos por hora. Se eles estão sendo gerados muito rápido, a dificuldade de gerar a prova-de-trabalho aumenta.
Rede
Os passos para rodar a rede são conforme a seguir:
- Novas transações são transmitidas para todos os nós;
- Cada nó coleta novas transações para dentro de um bloco;
- Cada nó trabalha para encontrar uma prova de trabalho difícil para seu bloco;
- Quando um nó encontra uma prova-de-trabalho, ele transmite o bloco para todos os nós;
- Os nós aceitam o bloco somente se todas as transações contidas nele são válidas e não foram gastas anteriormente;
- Nós de rede expressam a sua aceitação do bloco trabalhando na criação do próximo bloco na cadeia, usando o hash do bloco anterior que foi aceito como o hash anterior.
Nós de rede sempre consideram a maior cadeia como a correta e sempre continuarão trabalhando para estendê-la. Se dois nós de rede transmitem diferentes versões do próximo bloco simultaneamente, alguns nós de rede vão receber uma ou outra versão primeiro. Nesse caso, eles trabalham em cima do primeiro bloco que eles receberam, mas salvam o outro ramo no caso de ele se tornar maior do que o que está sendo trabalhado.
O consenso será alcançado quando a próxima prova-de-trabalho é encontrada e um dos ramos de blocos se torna maior, os nós de rede que estavam trabalhando no ramo que ficou menor, irão mudar para o ramo que se tornou maior.
Uma nova transação transmitida não precisa, necessariamente, alcançar todos os nós da rede. Desde que ela alcance muitos nós de rede, elas serão incluídas em um bloco mais tarde. Transmissões de blocos também são tolerantes com mensagens descartadas. Se um nó de rede não recebe um bloco, ele irá solicitá-lo quando ele receber o próximo bloco e perceber que um bloco está faltando.
Incentivo
Por convenção, a primeira transação em um bloco é uma transação especial, ela cria novas moedas que são possuídas como uma forma de recompensa pelo criador daquele bloco. Isso adiciona um incentivo para os nós de rede darem suporte e aderir à rede, além disso, provê uma maneira de distribuir inicialmente as moedas para a circulação, sem que haja uma autoridade central para emiti-las.
Uma adição estável de uma quantidade constante de novas moedas é análoga aos mineradores de ouro gastando seus recursos para colocar mais ouro em circulação. Em nosso caso, apenas poder computacional, tempo e eletricidade são gastos.
O incentivo também pode ser fundamentado através de taxas de transação. Se o valor de saída de uma transação é maior que o valor de entrada, a diferença desses valores é a taxa de transação que é adicionada como um valor de incentivo do bloco contendo a transação. Desde que o número pré-determinado de moedas tenha entrado em circulação, o incentivo pode ser dado inteiramente através de taxas de transações, mantendo o sistema completamente livre de inflação.
O incentivo irá ajudar a encorajar os nós de rede a se manterem honestos. Se um atacante ganancioso é capaz de reunir mais poder computacional do que todos os nós de rede honestos, ele teria de escolher entre usar seu poder para fraudar as pessoas roubando de volta seus pagamentos, ou usá-lo para gerar novas moedas. Ele iria achar mais lucrativo jogar conforme as regras, tais regras que o favorecem com mais moedas novas do que todos os outros juntos, do que prejudicar o sistema e a validade de sua própria riqueza.
Recuperando espaço em disco
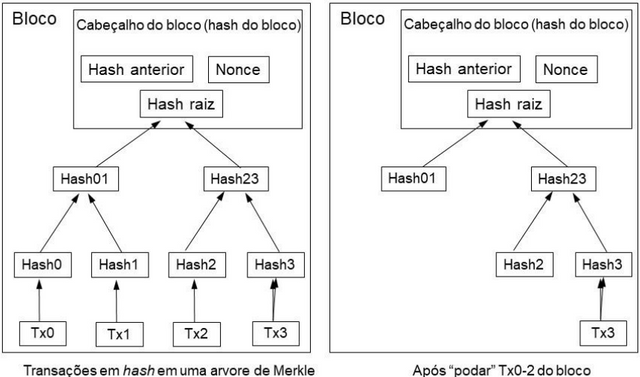
Desde que a última transação em uma moeda é garantida através uma quantidade suficiente de blocos, as transações gastas antes dessa última transação podem ser descartadas para guardar espaço no disco (hd) do computador. Para facilitar isso sem quebrar o hash do bloco, transações assumem seus hashes em uma Árvore de Merkle [7][2][5], com a única raiz incluída no hash do bloco.
Blocos mais antigos podem ser compactos podando os ramos desta árvore. Os hashes interiores não precisam ser armazenados.
Um cabeçalho de bloco sem transações teria o tamanho aproximado de 80 bytes. Se nós supomos que os blocos são gerados a cada 10 minutos, logo: 80 bytes * 6 * 24 * 365 = 4.2MB por ano. Atualmente os computadores estão sendo vendidos tipicamente com 2GB de RAM em 2008, e a Lei de Moore prevendo que o crescimento atual de 1.2gb por ano, o armazenamento não deverá ser um problema mesmo se os cabeçalhos dos blocos precisarem ser armazenados na memória.
Simplificando a verificação de pagamentos
Se é possível verificar pagamentos sem que seja necessário rodar um nó de rede inteiro. Um usuário precisa manter apenas uma cópia dos cabeçalhos dos blocos da cadeia que possua a maior prova-de-trabalho, a qual pode ser obtida consultando nós de rede até que ele esteja convencido de que ele tem a cadeia mais longa e obtenha o ramo da Árvore de Merkle vinculando a transação ao bloco com o registro de data e hora através de carimbos de tempo. Ele não pode checar a transação sozinho, no entanto, ele pode vincular ligando-a a um lugar na cadeia, dessa forma, ele pode ver se os nós de rede aceitaram a transação e se os blocos adicionados depois dela confirmam que a rede aceitou a transação.
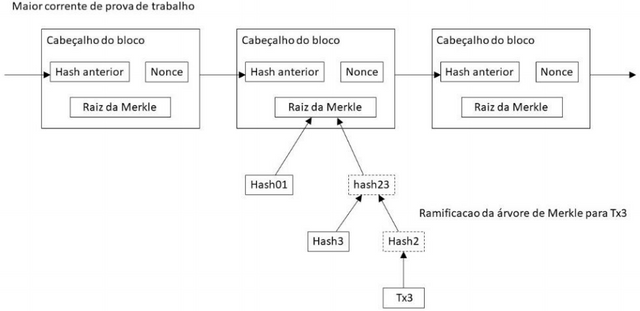
Assim sendo, a verificação é confiável enquanto os nós de rede honestos controlam a rede, mas ela pode se tornar vulnerável se a rede é controlada por um atacante. Enquanto os nós de rede podem verificar as transações por eles mesmos, um método simplificado pode ser enganado por transações forjadas pelo atacante enquanto a rede continuar sob seu domínio.
Uma estratégia para se proteger contra isso seria aceitar alertas de nós de rede quando eles detectam um bloco inválido, notificando o software dos usuários para baixar o bloco inteiro e as transações alertadas para confirmar a inconsistência. Estabelecimentos que recebem pagamentos frequentemente vão querer rodar seus próprios nós de rede para manter uma segurança mais independente e uma verificação mais rápida.
Combinando e dividindo valores
Embora fosse possível lidar com moedas individualmente, seria difícil fazer uma transação separada para cada centavo em uma transferência. Para permitir que o valor seja dividido e combinado, transações contém múltiplas entradas e saídas. Normalmente, haverá uma única entrada a partir de uma transação anterior maior ou entradas múltiplas combinando quantidades menores, e finalmente duas saídas: uma para o pagamento, e outra retornando o troco, que volta para o remetente do pagamento.
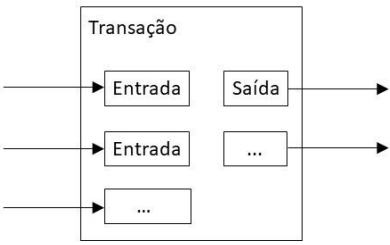
Deve-se notar que o número de entradas que podem ser conectadas a uma saída especificada, onde uma transação depende de várias transações, não há um problema aqui. Nunca há a necessidade de extrair cópia autônoma completa do histórico de uma transação.
Privacidade
O modelo bancário tradicional alcança um nível de privacidade limitando o acesso à informação das partes envolvidas e do intermediário confiável. A necessidade de anunciar todas as transações publicamente torna esse método inviável, mas a privacidade ainda pode ser mantida quebrando-se o fluxo de informações outro lugar: mantendo as chaves públicas anônimas.
O público pode ver que alguém está enviando uma quantia para outra pessoa, mas sem informações ligando a transação a ninguém. Isto é semelhante ao nível de informação divulgado pelas bolsas de valores, em que o tempo e o tamanho negócios individuais, a “fita”, é tornada pública, mas sem dizer quem eram as partes envolvidas na negociação.
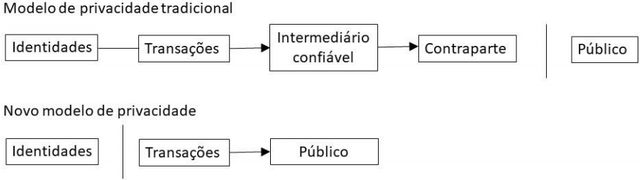
Como um firewall adicional, um novo par de chaves públicas precisaria ser usado para cada transação para evitar que eles sejam ligados a um dono comum. Alguma ligação ainda é inevitável com transações que tenham múltiplas entradas, as quais necessariamente revelam que suas entradas sejam possuídas pelo mesmo dono. O risco é que o dono da chave público seja revelado, caso isso aconteça, seria possível ligar todas as outras transações que foram feitas pelo mesmo dono.
Cálculos
Nós consideramos o cenário no qual um atacante está tentando gerar uma cadeia alternativa de blocos mais rápido que a cadeia honesta. Mesmo que isso seja feito, isso não torna o sistema aberto a mudanças arbitrárias, como criar valores do nada, ou tomar dinheiro que nunca pertenceu ao atacante.
Os nós de rede não irão aceitar uma transação inválida como pagamento, e nós honestos nunca vão aceitar o bloco contendo a transação fraudulenta. Um atacante pode apenas tentar mudar uma de suas próprias transações para tomar de volta o dinheiro que ele gastou recentemente.
A corrida entre a cadeia honesta e a cadeia atacante pode ser caracterizada como uma Caminhada Binominal Aleatória. O sucesso do evento ocorre quando a cadeia honesta está sendo estendida por um bloco, aumentando sua liderança em +1, e a falha do evento ocorre se a cadeia do atacante está sendo estendida, diminuindo o gap em -1.
A probabilidade de um atacante alcançar a cadeia honesta partindo de um dado déficit é análogo ao problema da Ruína do Apostador. Suponha que um apostador com crédito ilimitado comece com um déficit e jogue potencialmente um número infinito de tentativas para tentar alcançar o ponto de equilíbrio. Podemos calcular a probabilidade na qual o apostador atinge o ponto de equilíbrio, ou que um invasor alcance a cadeia de blocos honesta, como segue abaixo:
p = probabilidade um nó honesto encontrar o próximo bloco
q = probabilidade o atacante encontrar o próximo bloco
qz = probabilidade de o atacante se recuperar de z blocos atrás
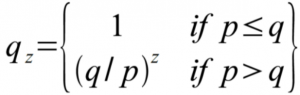
Dada a nossa suposição de que p>q, a probabilidade cai exponencialmente conforme o número de blocos que o atacante tem que acompanhar com o aumento da cadeia. Com as chances contra ele, se ele não tiver um lance de sorte logo no começo, suas chances irão se tornar cada vez menores conforme ele vai ficando para trás.
Nós vamos agora considerar o quanto a pessoa que recebe uma nova transação precisa esperar antes que tenha a certeza suficiente de que quem enviou a transação não pode mudar a transação. Nós supomos que quem enviou a moeda é um atacante que deseja fazer com que a pessoa que vai receber a moeda acredite que ele recebeu o seu pagamento naquele momento, e então reverter o pagamento de volta para ele mesmo depois de algum tempo. O destinatário da transação será alertado quando isso acontece, mas quem enviou a transação acredita que será tarde demais.
O destinatário gera um novo par de chaves e dá a chave pública para quem vai enviar as moedas por um curto momento antes de assinar. Isso impede que o atacante prepare uma cadeia de blocos com antecedência trabalhando continuamente até que ele tenha a sorte de chegar longe o suficiente, e então executar a transação no aquele momento.
Uma vez que a transação é enviada, o remetente desonesto começa a trabalhar em segredo em uma cadeia paralela contendo uma versão alternativa de sua transação. A pessoa que vai receber as moedas espera até que a transação tenha sido adicionada ao bloco e z blocos tenham sido ligados depois disso. Ele não precisa saber a quantidade exata de progresso que o atacante fez, mas supondo que a cadeia de blocos honestos tomou o tempo médio esperado por bloco, o progresso potencial do atacante será uma distribuição de Poisson com o valor esperado:
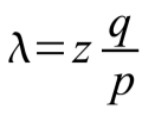
Para obter a probabilidade de um invasor ainda alcançar neste momento, nós multiplicamos a densidade de Poisson por cada quantidade de progresso que ele poderia ter feito pela probabilidade de ele conseguir alcançar a partir daquele ponto:
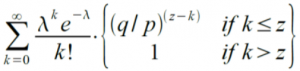
Reorganizando para evitar a soma de uma cauda infinita da distribuição…
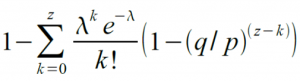
Convertendo em código C…
{
double p = 1.0 – q;
double lambda = z * (q / p);
double sum = 1.0;
int i, k;
for (k = 0; k <= z; k++)
{
double poisson = exp(-lambda);
for (i = 1; i <= k; i++)
poisson *= lambda / i;
sum -= poisson * (1 – pow(q / p, z – k));
}
return sum;
}
Executando alguns resultados, podemos ver a probabilidade cair exponencialmente com z.
q=0.1
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012
q=0.3
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
z=30 P=0.0001522
z=35 P=0.0000379
z=40 P=0.0000095
z=45 P=0.0000024
z=50 P=0.0000006
Para P menor que 0.1%
P < 0.001
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340
Conclusão
Propusemos um sistema para transações eletrônicas sem depender da confiança em intermediários. Nós começamos com o quadro usual de moedas feitas a partir de assinaturas digitais, que fornece um forte controle de propriedade, mas é incompleta sem uma maneira de evitar o gasto duplo.
Para resolver isso, nós propusemos uma rede ponto-a-ponto usando a prova de trabalho para registrar um histórico público de transações que rapidamente se torna computacionalmente impraticável para um atacante mudar, se nós honestos controlarem a maioria da potência computacional da rede. A rede é robusta em sua simplicidade não estruturada.
Nós de rede trabalham todos de uma vez com pouca coordenação. Eles não precisam ser identificados, pois as mensagens são não é roteado para qualquer lugar específico e só precisa ser entregue com base no melhor esforço. Nós de rede podem sair e voltar à rede à vontade, aceitando a cadeia de prova de trabalho como prova de que aconteceu enquanto eles estavam fora.
Eles votam com seu poder de CPU, expressando sua aceitação de blocos válidos, trabalhando em estendê-los e rejeitando blocos inválidos, recusando-se a trabalhar em eles. Quaisquer regras e incentivos necessários podem ser aplicados com este mecanismo de consenso.
Referências
[1] W. Dai, “b-money,” http://www.weidai.com/bmoney.txt, 1998.
[2] H. Massias, X.S. Avila, and J.-J. Quisquater, “Design of a secure timestamping service with minimal
trust requirements,” In 20th Symposium on Information Theory in the Benelux, May 1999.
[3] S. Haber, W.S. Stornetta, “How to time-stamp a digital document,” In Journal of Cryptology, vol 3, no
2, pages 99-111, 1991.
[4] D. Bayer, S. Haber, W.S. Stornetta, “Improving the efficiency and reliability of digital time-stamping,”
In Sequences II: Methods in Communication, Security and Computer Science, pages 329-334, 1993.
[5] S. Haber, W.S. Stornetta, “Secure names for bit-strings,” In Proceedings of the 4th ACM Conference
on Computer and Communications Security, pages 28-35, April 1997.
[6] A. Back, “Hashcash – a denial of service counter-measure,”
http://www.hashcash.org/papers/hashcash.pdf, 2002.
[7] R.C. Merkle, “Protocols for public key cryptosystems,” In Proc. 1980 Symposium on Security and
Privacy, IEEE Computer Society, pages 122-133, April 1980.
[8] W. Feller, “An introduction to probability theory and its applications,” 1957.
FONTE: https://foxbit.com.br/blog/whitepaper-do-bitcoin-portugues/
INSTAGRAM: https://www.instagram.com/mnegociacoes/
TWITTER: https://twitter.com/mnegociacoes
TELEGRAM FREE: https://t.me/joinchat/H6rquBHJLVhTZ_5HzhOphA