Geometría analítica y Cinemática (Parte XIV)
En primer lugar mi saludo respetuoso para toda la comunidad académica y científica de steemit, en especial a #stem-espanol, #steemstem, #utopian-io, #curie, #cervantes y #entropia, con su valioso apoyo hacemos posible nuestro crecimiento en todos los aspectos relacionados a esta prestigiosa plataforma y además nos permiten resaltar la extraordinaria e grandiosa labor de la ciencia ya que nos olvidamos de su incalculable valor para la existencia de la humanidad.
Continuamos con la temática geometría aquella que articulada al lenguaje abstracto del álgebra consolidan el extraordinario carácter analítico de las matemáticas, fundamental característica implementada para el análisis del esencial nexo entre la majestuosa ciencia física y las indispensables matemáticas. Podemos expresar claramente con cada uno de los análisis antes realizados que el espléndido campo de la ciencia nos ha ofrecido todas y cada una de las herramientas necesarias para poder entender cualquier tipo de fenómeno que de desarrolle en nuestro alrededor tal y como lo hace con el extraordinario fenómeno del movimiento a través de ramas de la ciencia como la cinemática y la geometría analítica.
Es importante poder seguir expresando el propósito primordial de cada uno de estos artículos el cual no ha sido otro que el de conocer de forma general el comportamiento de importantes movimientos presentes entre nosotros, y los cuales juegan un vital papel tanto en nuestro desarrollo como para nuestra existencia, por tanto podemos nombrar los fenómenos de movilidad estudiados hasta el momento encontrándonos de esta manera con los movimientos tales como; el circular, parabólico, elíptico, hiperbólico, rectilíneo-curvilíneo, oscilatorio, vibratorio, ondulatorio, caótico, armónico complejo, armónico forzado amortiguado, movimiento cicloidal, epicicloidal ,extraordinarios fenómenos de movilidad intrínseca tal como el movimiento periódico que a su vez representa un esencial aspecto del reconocido movimiento armónico simple (M.A.S.) representando este último el más destacado e importante modelo entre los fenómenos oscilatorios, y por supuesto resaltando siempre el hecho que nos indica que cualquier partícula, cuerpo u objeto al describir dichos movimientos transitarán por el lugar geométrico de algún tipo de forma o de figura diseñada por nuestra geometría analítica y su excelente lenguaje abstracto.
En pasadas publicaciones analizamos el movimiento de una circunferencia sobre una línea recta a velocidad constante, sin deslizarse, obteniendo a la conocida curva cicloide y sus importantes características, luego hicimos rodar dicha circunferencia no sobre una línea recta sino sobre otra circunferencia (movimiento de forma exterior) este hecho particular caracteriza la utilización del prefijo Epi y se refiere cuando algo se encuentra sobre otra cosa como es el caso de cada una de las curvas Epicicloidales, en donde conocimos curvas como la cardiode y nefroide entre otras.
Ahora haremos rodar o girar esta circunferencia pero en esta ocasión por el interior de otra circunferencia (movimiento de forma interna), por lo tanto podemos decir que dichas curvas resultantes se diferencian de las epicicloides en relación al movimiento y lugar por donde gira la circunferencia que denominaremos generatriz ya que la misma lo hará por la parte interior de la circunferencia directriz o fija de un determinado circulo generando de esta manera importantes curvas de la familia hipocicloidal.
Por lo tanto al tener una circunferencia de un círculo grande de manera estática o fija y por dentro de la misma encontramos a otra circunferencia pequeña girando por todo el interior de la circunferencia del circulo fijo entonces podemos decir que cualquier punto perteneciente a la circunferencia generatriz o móvil podrá describir la figura de la curva llamada hipocicloide, teniendo en cuenta que si el radio de la circunferencia directriz o fija es 2, 3, 4 o n veces mayor que el de la circunferencia móvil entonces nos encontraremos con curvas hipocicloidales con 2 , 3 , 4 ó n puntas respectivamente.
Entonces desde el punto de vista geométrico podemos expresar que una hipocicloide representa el lugar geométrico de las diferentes posiciones de cualesquier punto correspondiente a la circunferencia de un círculo y la cual gira, da vueltas o rueda de forma interior, y sin resbalar, en la circunferencia de otro circulo fijo de mayor tamaño y dependiendo de la proporción existente entre los radios de las circunferencia involucradas (tanto móvil o generadora como fija o directriz) podemos conseguir distintas curvas pero cada una de ellas pertenecientes a la misma familia conocidas como hipocicloides.
Para conocer la longitud de esta curva es importante recordar que en el caso de la cicloide al igual que la línea recta sobre la cual la misma se genera ambas son infinitas y que por tanto no podíamos determinar su longitud total (de la cicloide), en cuanto a las curvas epicicloidales pudimos notar que resultaban ser acotadas o delimitadas igual que la circunferencia fija sobre la cual giraba la otra circunferencia generatriz, en donde dichas curvas junto a la longitud de cada uno de sus arcos obtendríamos su longitud total, de manera similar resultaría el cálculo de la longitud total de la curva hipocicloidal ya que al igual que las epicicloides dependerá de la proporción entre los radios de las dos circunferencias relacionadas y esto como expresamos definirá la cantidad de arcos o puntas de la hipocicloides y en consecuencia en la longitud total de tal extraordinaria curva.
Podemos evidenciar que debido a la implementación del fenómeno del movimiento pudimos conocer o generar las extraordinarias curvas hipocicloidales, ya que debido al desplazamiento de la figura geométrica denominada circunferencia (generatriz) la cual gira o rueda tangencialmente en el interior de otra (directriz) hemos podido establecer el lugar geométrico para estas hipocicloides.
Estas curvas también al igual que las epicicloides las conocemos con el nombre de curvas cíclicas, de rodaduras o de formas más práctica curvas mecánicas por su estrecha relación en la fabricación de piezas para mecanismos de transmisión de movimientos, entonces podríamos expresar que estas curvas son elementales al momento de diseñar dientes para engranajes guardando desde este punto de vista una estrecha relación con sus curvas primas, las epicicloidales, a pesar que la orientación de estas dos familias de curvas resulten de sentido opuesto y claro está por el sentido como rueda la circunferencia generatriz ya que para la generación de unas curvas lo hace en el exterior de otra circunferencia y para las otras lo realiza en el interior de la circunferencia como se ha mencionado anteriormente.
Los engranajes epicicloidales representan un claro ejemplo en cuanto a la relación existente con las curvas hipocicloidales debido a que los engranajes externos los cuales giran sobre un engranaje central también giran de manera interna y tangencialmente en un engranaje de tipo anular el cual representa una corona para tales engranajes satélites si tomamos en cuenta su denominación de engranajes planetarios como lo observamos en la pasada publicación.
De la ciencia de las formas y las figuras, es decir, geométrica analítica, seguimos adquiriendo todos aquellos lugares geométricos utilizados al transitar cualquier partículas, cuerpos u objetos cuando lleva a cabo un determinado fenómeno de movilidad y esto lo hemos comprobado en cada uno de los anteriores artículos, en donde podemos afirmar que nos hemos deslizado a través de importantes trayectorias las cuales se encuentran relacionadas con destacables y reconocidas figuras geométricas como la línea recta, la circunferencia, la parábola, la elipse, la hipérbola, combinación de tales figuras, al igual que alguna porción de ellas, también conocimos otras figuras muy complejas como la mariposa o atractor de Lorentz, curvas periódicas o armónicas, la cicloide, las epicicloides, en donde cada una de estas formas o figuras constituyen a un tipo de movimiento bien sea de manera particular o compuesta, y de manera general compleja.
Partiendo del punto de referencia de la curva cicloide y recordando que la misma se genera a través de un punto fijo de una circunferencia que gira o da vueltas, sin deslizarse, y a velocidad constante sobre una línea recta, y que dicha curva al invertirla adquiría propiedades importantes como la braquistócrona y tautócrona, pero seguimos haciendo rodar la circunferencia pero ya no sobre una línea recta sino sobre otra circunferencia y obtuvimos las extraordinarias curvas epicicloidales y todo lo que dichas curvas representan en el campo del diseño de piezas para engranajes y transmisión de movimientos.
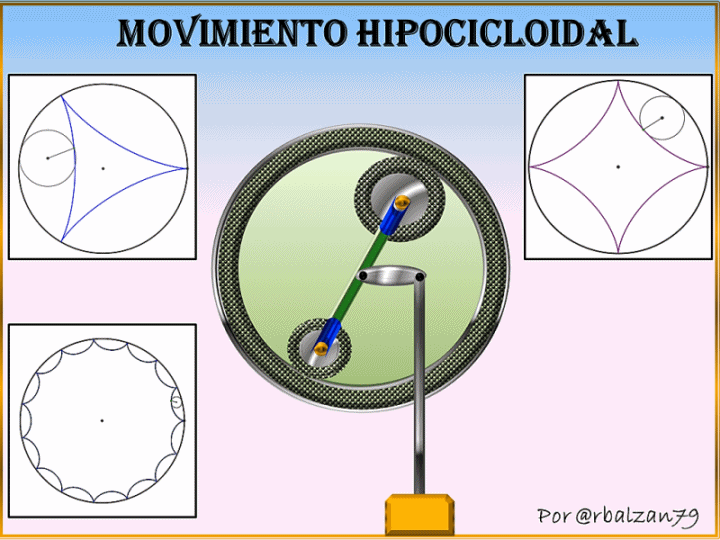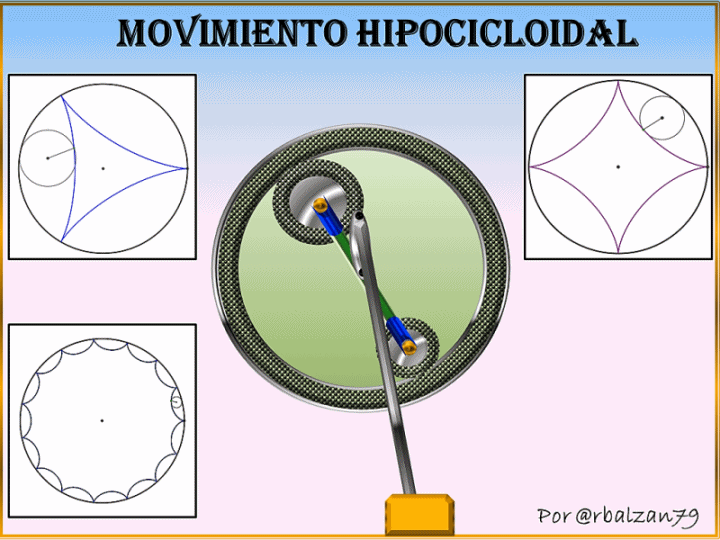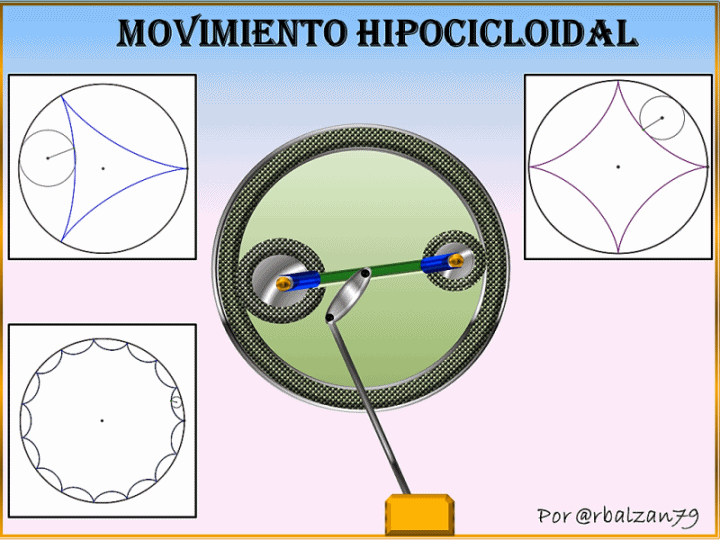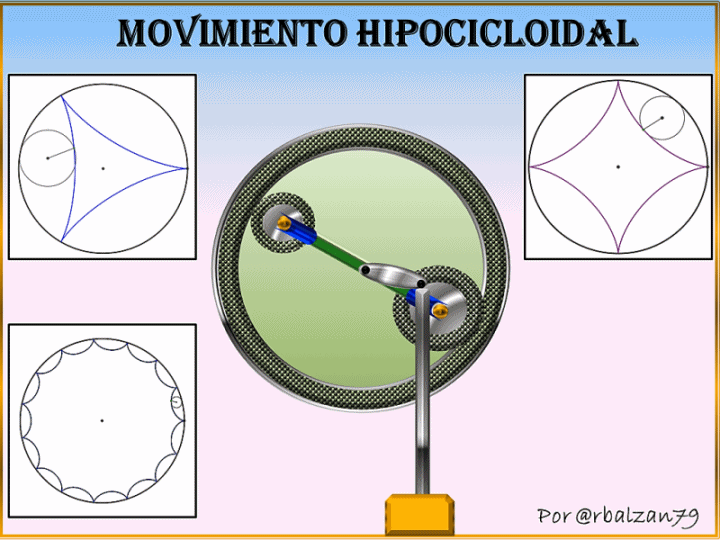
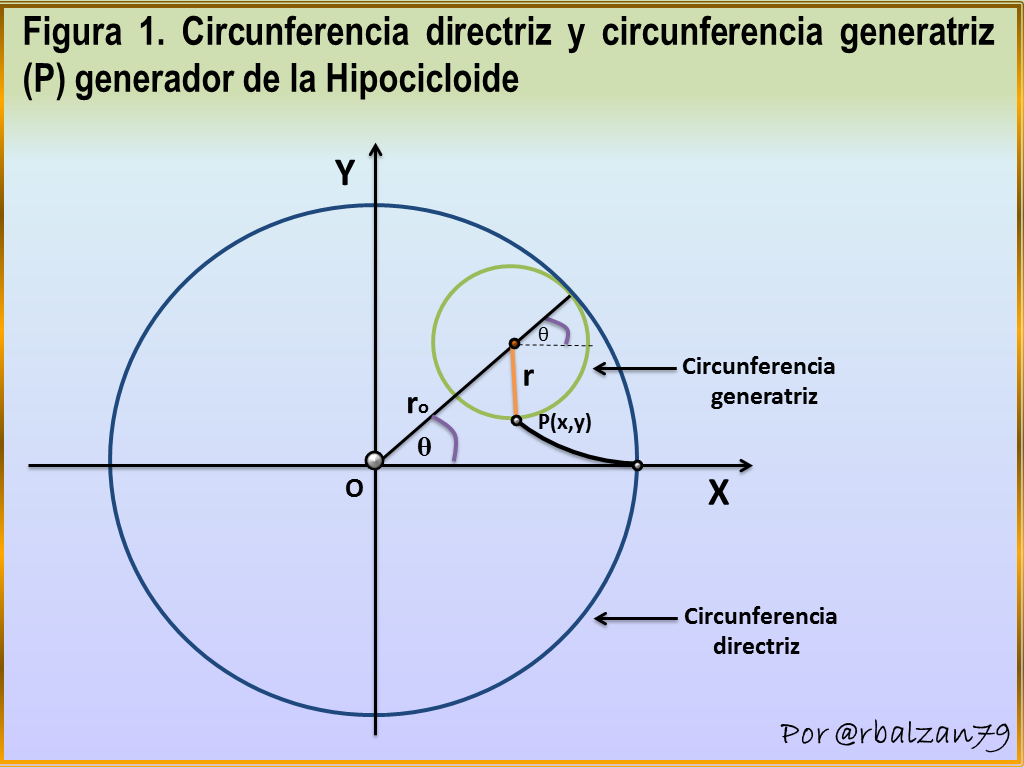
En esta ocasión nuestra circunferencia generatriz la haremos girar tangencialmente en el interior de otra circunferencia con la finalidad de generar las curvas hipocicloidales como podemos observar en la siguiente figura 1.
En la figura 1 podemos notar como se inicia la formación de un tipo de hipocicloide teniendo en cuenta la proporción entre los radios de las circunferencias relacionadas, es decir, móvil (generatriz) y fija (directriz) ya que de esto dependerá el tipo y la forma de la hipocicloide, por lo tanto si tenemos que el radio de la circunferencia fija o directriz es 2, 3, 4 o hasta n veces mayor que el radio de la circunferencia móvil entonces tendremos hipocicloides con 2, 3, 4 y así respectivamente como podemos observar en los siguientes gif animados comenzando con la curva hipocicloidal denominada deltoide o de tres (3) puntas.
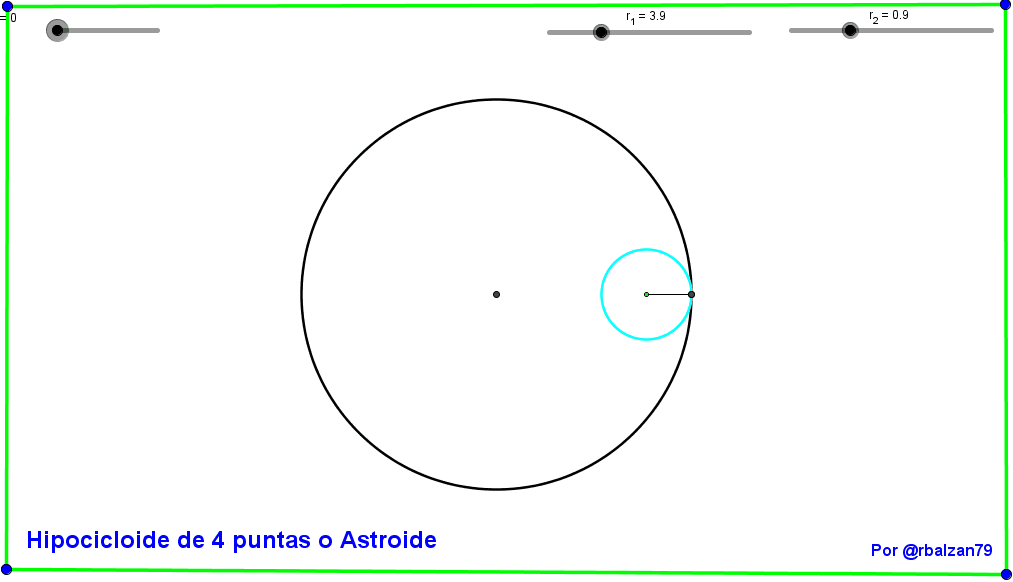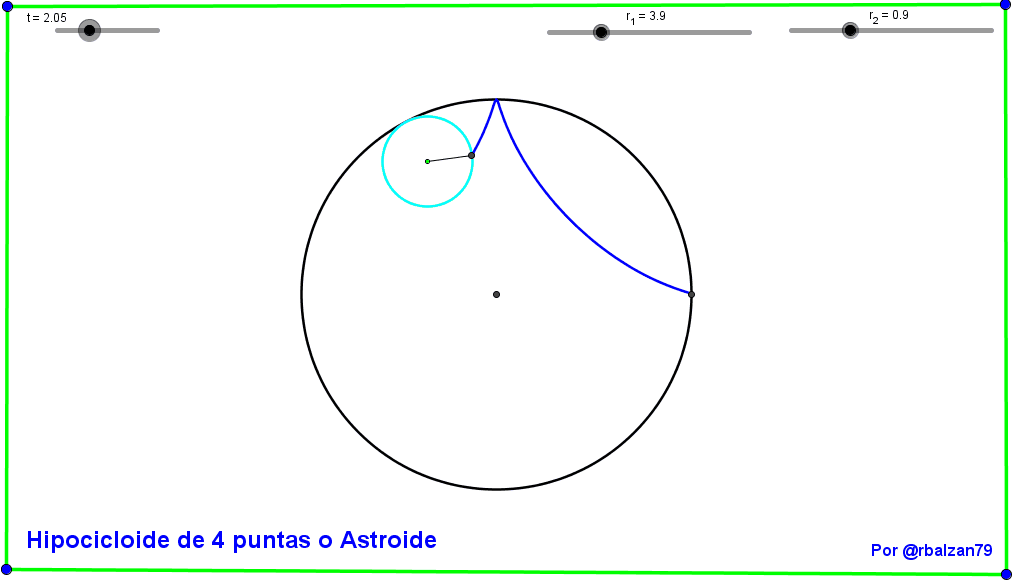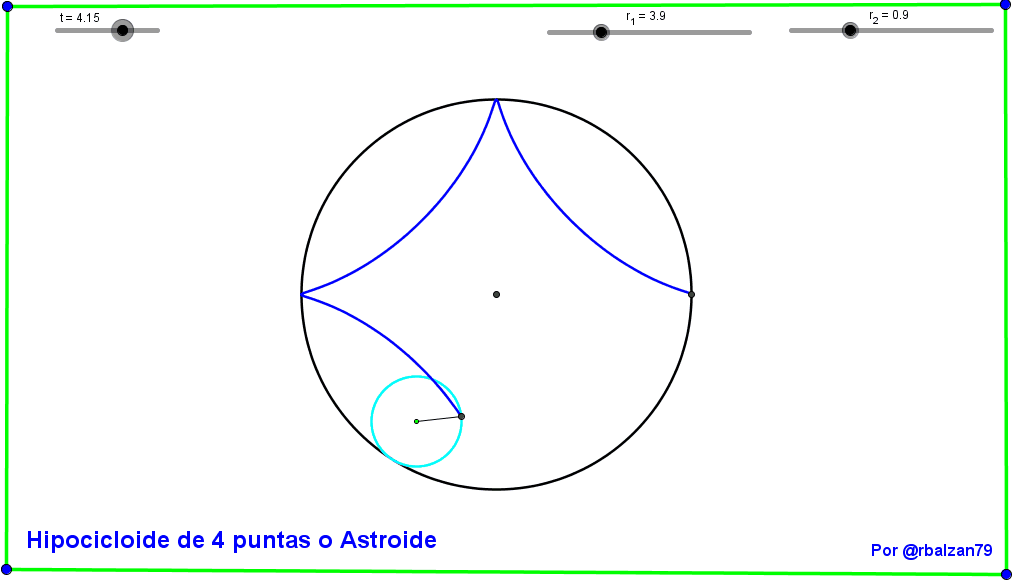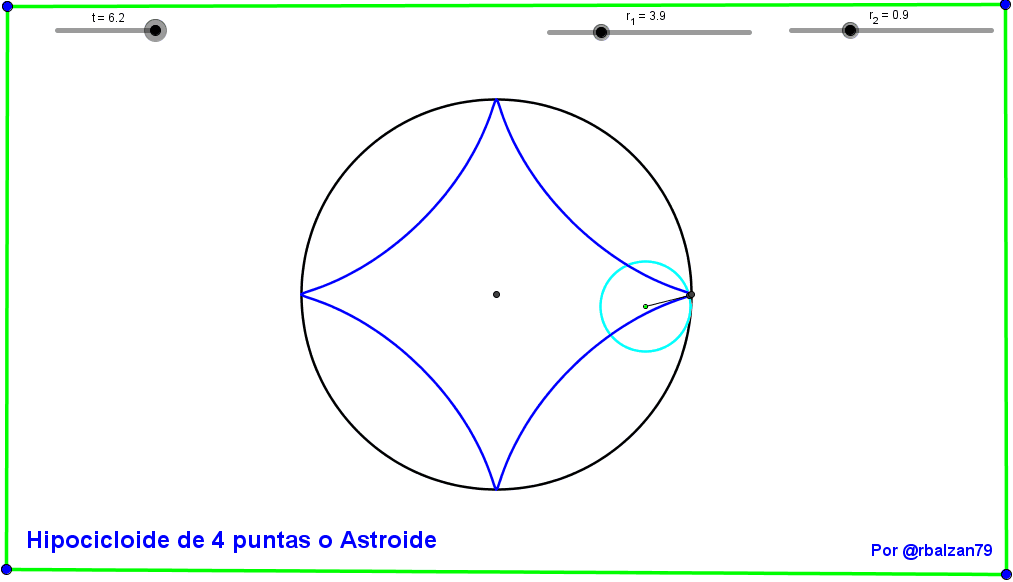
Seguimos ahora con nuestro segundo gif animado y la conformación de la hipocicloide llamada Astroide (por su parecido a una estrella) o de cuatro (4) puntas como podemos ver a continuación:
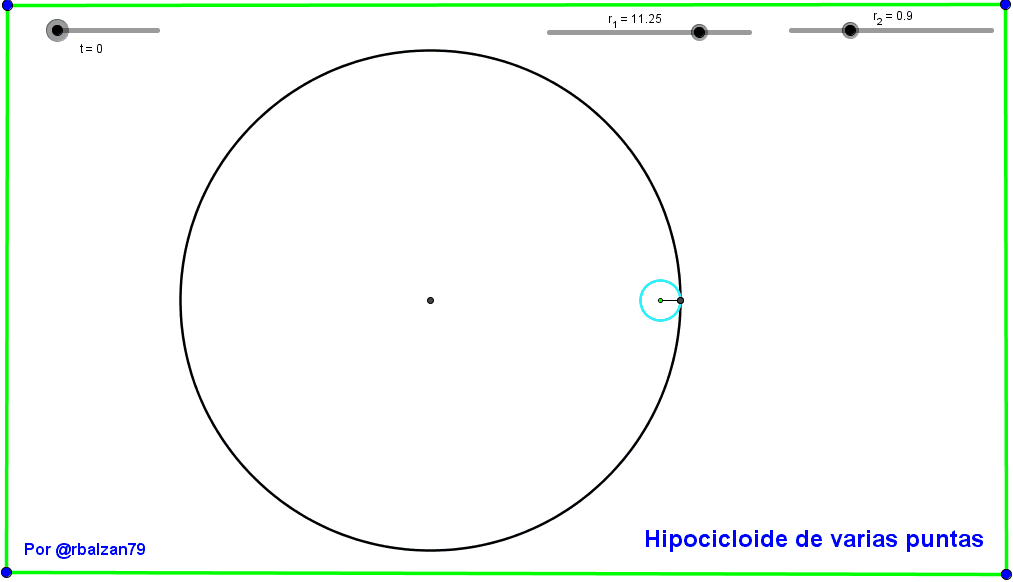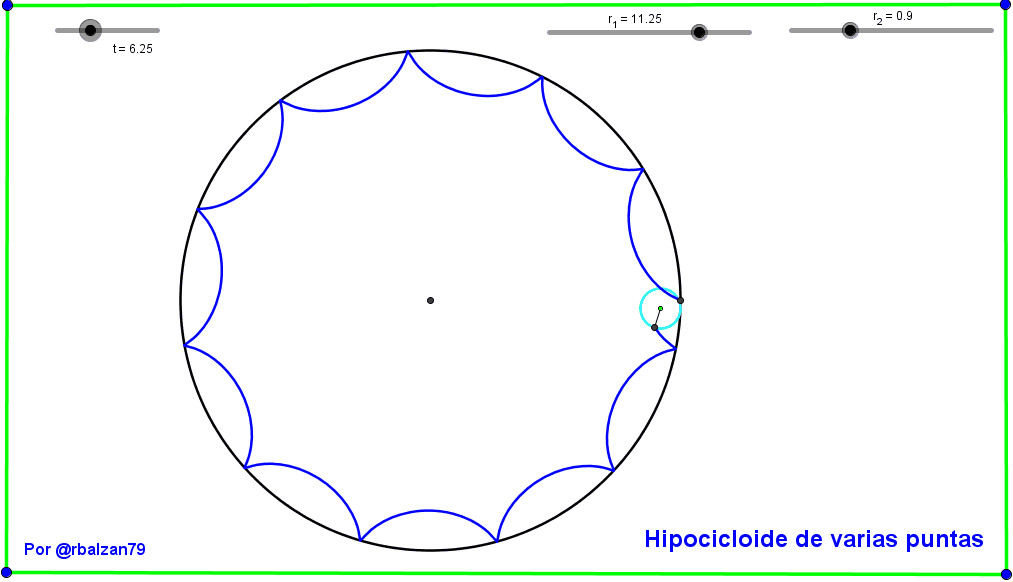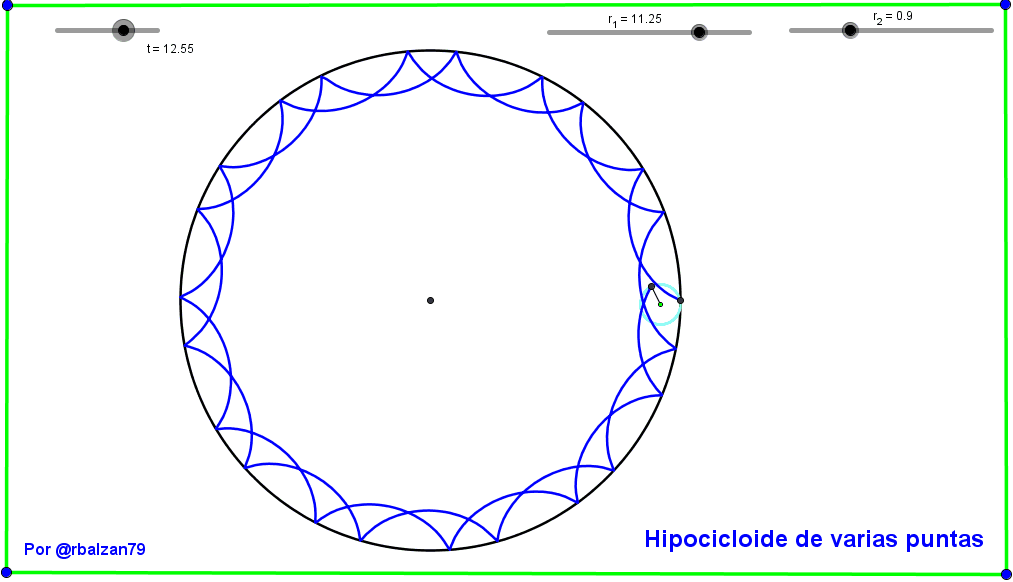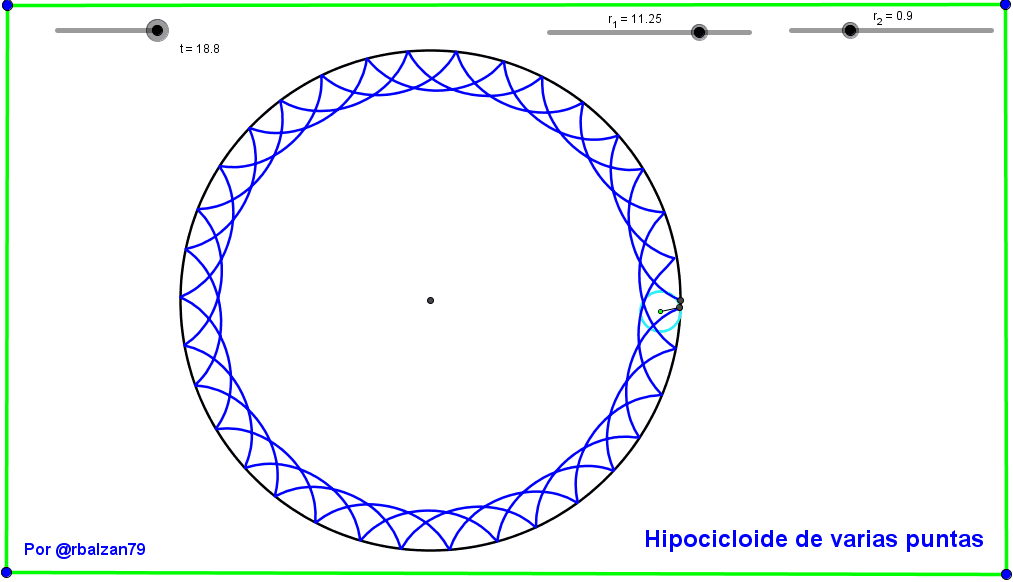
Ahora continuamos con otro tipo de curva hipocicloidal aquellas con varias puntas debido a su mayor grado de complejidad en cuanto a la proporción o razón entre los radios de las circunferencias involucradas como podemos observar a continuación en el siguiente gif animado:
Con los anteriores movimientos certificamos la utilidad de dicho fenómeno en la creación de importantes curvas dentro del mundo de la geometría analítica y que a su vez se convertirán en excelentes trayectorias a seguir por cualquier partícula, cuerpo u objeto mientras desarrollan un particular o complejo movimiento.
# ***Movimiento Hipocicloidal***
Seguimos encontrando innumerables tipos de movimientos presentes en nuestro magnifico entorno en donde se desarrolla nuestra existencia, y el movimiento hipocicloidal representa uno de estos esenciales fenómenos de movilidad que nos ha permitido elevar nuestro nivel intelectual y en consecuencia social, pero si hablamos de la creación o generación de las distintas curvas hipocicloidales nos encontraremos que para tal propósito es necesario llevar a cabo un determinado movimiento, dicho movimiento es el que pudimos observar de forma práctica en cada uno de los anteriores gif animados en donde una circunferencia rueda o gira por el interior de otra de manera tangencial dando como resultado cada una de las curvas ya descritas y muchas otras más pertenecientes a la amplia familia de las hipocicloides.
Podemos decir que gracias al movimiento hemos podido descifrar importantes curvas como lo es la cicloide y al seguir haciendo girar la circunferencia generatriz pudimos ampliar y conoces otras curvas relacionadas a la cicloide pero anteponiéndoles tanto el prefijo Epi, el mismo está relacionado a la acción de girar la circunferencia sobre otra en el caso de las epicicloides y en esta oportunidad Hipo prefijo el cual indica por debajo de algo como en el caso de las hipocicloides en donde la circunferencia ahora rueda tangencialmente pero en el interior o por debajo de otra circunferencia.
Es muy importante resaltar de esta curva su carácter cíclico debido a que su trayectoria se repite cíclicamente y al igual que las epicicloides juegan un esencial papel en el diseño de piezas para engranajes por lo que también se les denomina curvas mecánicas, y así toda su relación en cuanto a la transmisión de innumerables tipos de movimientos encontrándonos principalmente con el circular por la movilidad que representa una o varias ruedas dentro de otra como podemos visualizar en el gif al inicio de este artículo.
Por tanto la implementación de un movimiento de tipo hipocicloidal ha permitido profundizar en el desarrollo de cualquier tipo de mecanismos con los cuales es posible generar otro tipo de movilidad y con ello ayudar a reducir enormemente nuestras labores cotidianas, ya que nuestras vidas dependen y dependerán de cualquier tipo de movimientos como el analizado en esta oportunidad y el cual marca sus huellas en el majestuoso campo de la ciencia a través de la geometría analítica y la cinemática.
Siempre que nuestros ojos puedan observar un movimiento de una rueda dentro de otra ya sabemos que el fenómeno desarrollado es el hipocicloidal sin importar la actividad desarrollada en ese momento, en ciertas ocasiones nos encontramos con la audacia de acróbatas rodando con sus motocicletas dentro de una esfera que si lo observamos desde un plano rectangular frontal y dicha motocicleta girando en el interior del círculo notaremos que las ruedas de tal sistema mecánico (motocicletas) originaran hipocicloides y con ello llevando a cabo cada una de las partículas presentes en las ruedas un movimiento hipocicloidal.
La utilidad de cada uno de los modelos matemáticos cada vez más se han hecho sentir en el mundo de la ciencia, y como no hacerlo si los mismos nos han permitido la interpretación abstracta de los distintos tipo de fenómeno que se desarrolla en nuestra naturaleza, para esta ocasión conoceremos algunos modelos algebraicos utilizados en la conformación del lugar geométrico de la extraordinaria curva hipocicloidal, representando de esta manera dicha curva otra importante herramienta complementaria para la consolidación del conocimiento acerca de imprescindible fenómeno del movimiento.
La hipocicloide representa aquel lugar geométrico que describe un determinado punto de una circunferencia (generatriz) la cual rueda o gira por debajo de otra circunferencia fija (directriz), para conocer el ángulo del arco directriz podemos implementar al igual que en la epicicloide la siguiente formulación:
Mediante la ecuación 2 calculamos la longitud de un arco de una determinada hipocicloide y con la 3 la longitud total de toda la curva hipocicloidal, notando la importancia entre la relación entre los radios de las circunferencias directriz y generatriz como lo comprobamos en cada uno de los gif ya que mientras más pequeño sea el radio de la circunferencia generatriz en relación a la de la circunferencia directriz, mayor serán los arcos de la hipocicloide.
Continuamos describiendo algunas ecuaciones relacionadas con la curva hipocicloide por lo tanto tomamos como referencia a la figura 1, y de esta manera determinar las formulaciones relacionadas a las coordenadas del punto generador de la hipocicloide, por tanto tenemos:
Los imprescindibles modelos matemáticos han reducido el alto grado de complejidad presentes en nuestros fenómenos naturales con la firme intención de poder brindar tanto a la ciencia como a cualquier persona un mejor entendimiento de forma generalizada de dichos fenómenos.
Son innumerables las distintas formas de manifestación del fenómeno del movimiento pero cada una de ellas son un importantes y vitales herramientas tanto para el crecimiento de toda especie viviente como del mismo universo, la curva hipocicloidal al igual que cualquier que otras curvas se configuran a través de un determinado movimiento como el desarrollado durante la creación de esta curva mediante el movimiento de dos circunferencia una denominada directriz que es en donde descansa o rueda la otra llamada generatriz.
Por lo tanto podemos notar la clara relación existente entre la cinemática con la geometría analítica consolidándose tal nexo mediante la implementación de cada una de las figuras estructuradas a través de la geometría en el análisis y estudio del fenómeno del movimiento en pleno, y esto lo hemos observado en las trayectorias seguidas por cualquier partícula, cuerpo u objeto al transitar el lugar geométrico de una determinada figura cuando realiza o lleva a cabo un particular o compuesto movimiento.
Muchos son los tipos de hipocicloides que se generan al rodar una circunferencia dentro de otra por lo que es importante tener en cuenta es la relación entre los radios de dichas figuras circulares ya que esta proporción determinará la cantidad de arcos o puntas de una hipocicloide como lo pudimos observar en cada uno de los gif presentados anteriormente, en donde conocimos a la deltoide, astroide y una hipocicloide con varios arcos o puntas, por tanto mientras más reducida sea la circunferencia generadora con respecto a la fija o directriz podemos obtener curvas hipocicloidales con gran número de puntas.
El movimiento antes descrito y el cual se origina entre ambas circunferencia es utilizado como ejemplo en el diseño de importantes sistema de transmisión de movimientos y la curva generada, la hipocicloidal, ha servido como base para el diseño o fabricación de piezas mecánicas y de allí también su nombre como curvas mecánicas al referirse a toda la familia hipocicloidal, por lo tanto podemos decir que una de las aplicaciones más relevantes de estas extraordinarias curvas es para la elaboración de formas de los perfiles de cada uno de los dientes de una determinada rueda que compone un sistema de engranaje.
Por tanto la curva en si como el movimiento generado por un punto de una circunferencia mientras rueda tangencialmente por debajo de otra, sin deslizarse, al cual hemos denominado hipocicloidal son de gran interés en el mundo de la física en especial en el área de la mecánica por su estrecha relación con los engranajes (por el diseño de los perfiles de los dientes) y los sistemas de transmisión de movimientos compuesto principalmente por estos elementos dentados.
Para concluir mis apreciados lectores es importante conocer sobre cualquier tipo de fenómenos de movilidad ya que de los mismos siempre extraeremos cualquier tipo tanto de conocimientos como de utilidad para nuestras actividades cotidianas logrando de esta forma una mayor estabilidad social, agradeciendo siempre al nexo existente entre la geometría analítica y la cinemática las cuales como hemos expresados nos permiten estar cada vez más cerca de nuestro entorno natural.
Hasta otra oportunidad mis apreciados lectores de steemit, en especial a los miembros de la gran comunidad de #STEM-Espanol, los cuales reciben el apoyo de otras tres grandes comunidades como los son #steemstem, #utopian-io y #curie, por lo cual recomiendo ampliamente formar parte de este hermoso proyecto, ya que resalta la valiosa labor de la academia y del campo científico, pero sobre todo, por el gran respecto, dedicación y ayuda para sus miembros.
Nota: Todas las imágenes fueron elaboradas usando las aplicaciones Paint, Power Point, los gif de las curvas hipocicloidales fueron realizadas con GeoGebra y el gif animado al principio de la publicación fue elaborado con la aplicación de PhotoScape.
[1] Charles H. Lehmann. Geometría Analítica. Décima tercera reimpresión. Editorial Limusa. México, D.F. 1989.
[2] Jennings, G.A. Geometría moderna con aplicaciones. Springer, New York, 1994.
[3] Snapper, E., Troyer, R.J. Geometría afín métrica. Dover, New York, 1971.
[4] Raymod A. Serway y John W. Jewett, Jr. Ed. Thomson. Física. Edición 1 y 3.
[5] Giancoli, D.C. Física, principios y aplicaciones, Reverté S.A. España, 1985.
[6] Casasco Juan Patricio, Valoni Andres, Romani Julieta. Cicloide. Universidad Favaloro. Julio 2001.
[7] Arriagada Sandoval Camila. Modelos Matemáticos. Universidad del BÍO-BÍO. Chillan, 2015.
[8] Corcho Gutiérrez Fernando Manuel. La cicloide. Universidad de Sevilla, Facultad de Matemáticas, año 2017.
[9] Lafuente J. Geometría diferencial de curvas en el plano. Enero de 1998.








¡Felicitaciones!
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
Puedes consultar el reporte diario de curación visitando @entropia.
Te informamos que el PROYECTO ENTROPÍA ha creado un nuevo servicio, la Creación de cuentas nuevas de Steemit, para más información puedes visitar este enlace.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Gracias por el apoyo amigos. Saludos.
Gracias al curador @ramonycajal por el apoyo así como a toda la comunidad de cervantes. Saludos.
Estamos dando votos DIARIOS de entre 0.05$ y 0.10$ a todos los que se metan en el TRAIL de @inteligentzia en steemauto.com, aprovecha ahora! Contactame por Discord si necesitas mas informacion
Te dejo un post tutorial: https://steemit.com/spanish/@inteligentzia/unete-al-trail-de-inteligentzia-y-te-damos-votos-diarios-con-valor-de-0-05usd
Gracias por el apoyo. Saludos.
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @utopian-io.
If you appreciate the work we are doing, then consider supporting our witness stem.witness. Additional witness support to the curie witness and utopian-io witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for having added @steemstem as a beneficiary to your post. This granted you a stronger support from SteemSTEM.
Thanks for having used the steemstem.io app. You got a stronger support!
Thanks to the communities of @SteemSTEM, @utopian-io and @curie for the support received.
Hi @rbalzan79!
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV