Matrix Multiplication Inches Closer to Mythic Goal - Quantamagazine

^{( March 23, 2021; Quantamagazine )}

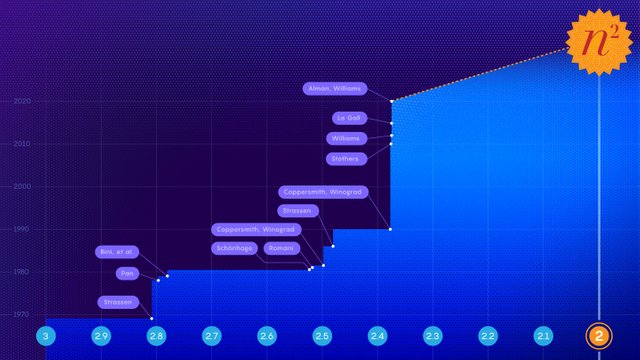
For this reason, the fastest one could possibly hope to multiply pairs of matrices is in n² steps — that is, in the number of steps it takes merely to write down the answer. This is where “exponent two” comes from.

And while no one knows for sure whether it can be reached, researchers continue to make progress in that direction.

A paper posted in October comes the closest yet, describing the fastest-ever method for multiplying two matrices together. The result, by Josh Alman, a postdoctoral researcher at Harvard University, and Virginia Vassilevska Williams of the Massachusetts Institute of Technology, shaves about one-hundred-thousandth off the exponent of the previous best mark. It’s typical of the recent painstaking gains in the field.

When "inches" is an exaggeration. ; -)

The new record is n^2.3728596, and it's actually Vassilevska's second time creating the fastest known method. Her previous time, in 2012, was bested in 2014 by François Le Gall.

The researchers accomplished this improvement by tweaking the "laser method" family of algorithms, first developed in the 1970s. This method works by translating matrix multiplication into equivalent problems involving tensors. But this latest work may have maxed that technique out. Instead, according to Chris Umans - from the California Institute of Technology, getting to n² would probably require discovery of a new method.

Read the rest from Quantamagazine: Matrix Multiplication Inches Closer to Mythic Goal