The importance of good, precise definition of terms

In mathematics, definitions are our lifeblood. Mathematicians strive for precision.

Philosopher vs Mathematician

If one asks questions, one should make sure that the definitions of the terms in the questions are properly understood.

Philosopher: What is the purpose of my existence?

• I have no idea; neither of the nouns in this question can be defined with any precision. We have to ask. What is purpose to you? How do you quantify that purpose? What is existence? What are the conditions for you to exist?

Mathematician: Is the square root of 2 a rational number?

• Absolutely not! We can answer this kind of question with precision because we know precisely what is meant by the phrases “square root of 2” and “rational number”

When it comes to proving our assertions, claims, and arguments it is easier if we have agreed upon on the “right” definitions.

Definitions evolve over time and some definitions are modified to fit some assertions only to realize that its modification results to even better assertions and hence has to be adapted. However, when more than one definition exists for the same idea Mathematician has to settle for a standard one.

Take for example the definition of prime numbers.

• Definition 1. A prime number is a positive integer, greater than 1, whose only factors are 1 and itself.

• Definition 2. A prime is a quantity p such that whenever p is a factor of some product ab, then either p is a factor of a or p is a factor of b.

We can formulate many equivalent definitions for some concept. If this happens one can use TFAE, “the following are equivalent”, which requires a proof, showing that different statements actually define the same concept.

Since we are talking about prime numbers in this post, it seems reasonable to make some explorations on what a prime number is.

Fundamental theorem of arithmetic

Prime numbers act as multiplicative building blocks for the rest of the integers.

Disassembling an integer into its building blocks is called prime factorization of that number. Prime factorizations are unique for each number; that is, a number is either a prime or it has prime factors (probably raised to various powers) that are uniquely determined - except that they may be re-ordered.

A decomposition of a number n into prime numbers is given by:

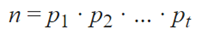
where the p1, p2, p3, p4 to pt is called the prime factorization of n.

Looking for Prime Numbers:

Eratoshenes of Cyrene was a Greek mathematician and astronomer who is famous for his “sieve” method for finding primes. Until now, the sieve of Eratoshenes is still important in some mathematical research.

Here’s the method:

It is consists of creating a very long list of natural numbers and then crossing off all the numbers that aren’t prime. It is carried out in stages,

1. circle 2 and then cross off every number that has 2 as a factor, we have identified 2 as a prime number and eliminated those numbers that aren't prime
2. at this stage, 3 was not eliminated we then circle it again indicating as the second prime number, we then identify those that have 3 as a factor. (note some factors are crossed twice)
3. repeat this process for 5, 7 and so on
4. what remains are the prime numbers

Sieve of Erastothenes

The way prime numbers are distributed amongst the integers is very erratic. Prime number theorem describes the distribution of prime numbers in large values. It quantifies the rate at which the prime numbers become rare as it becomes larger and larger

Unsolved Mysteries of prime numbers

Several historical questions regarding prime numbers are still unsolved. Landau's four problems concerning prime numbers are still unsolved. They actually sound easy.

• Goldbach’s conjecture

Can every even integer greater than 2 be written as the sum of two primes?

• Twin prime conjecture

Are there infinitely many primes p such that p + 2 is prime?

• Legendre's conjecture

Does there always exist at least one prime between consecutive perfect squares?

• (insert_your_name conjecture)

Are there infinitely many primes of the form n^2 + 1?

Applications of Prime Numbers

Primes are used in several fields of studies that require difficulty of factoring large numbers into prime numbers, this includes:

• pseudorandom number generators
• public-key cryptography algorithms
• evolutionary strategy in biology

Other explorations on prime numbers

Various conversions of prime numbers into something that make sense (pun intended)

1. Visualization of Prime Numbers
2. Music of Prime Numbers

References:

1. https://en.wikipedia.org/wiki/Prime_number#Other_mathematical_applications
2. A Gentle Introduction to the Art of Mathematics by Joe Field

---

Thank you for reading ...