Analytical Geometry and Algebra - Projection of a straight line .lesson # 1
Hello friends, welcome ...
In this present publication we will talk about the projection of a line, distance between two points and points aligned on a line, in this sense we start talking about what are the projections?
The projections of a line can be obtained through the projections of two points belonging to that line.
The lines perpendicular to a projection plane have a projection of a point on that projection plane.
The lines are infinite, although for a better understanding of the subject, we consider the lines defined by segments, which we will project in different positions.
Then we will present some images, where graphically we can observe the line drawn in each phase that we will explain here.
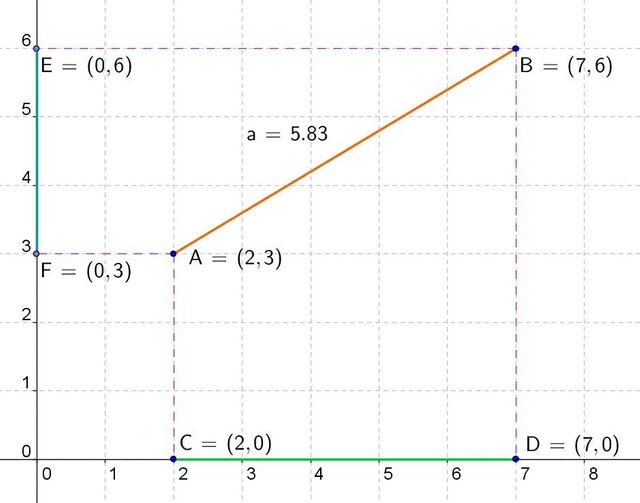
The projection of a segment on the abscissa axis whose ends are points 2,3 and 7,6, is a segment that has respectively 2.0 and 7.0 coordinates. The coordinates of the segment on the horizontal axis are the coordinates corresponding to the x of both points, that is, the distance of the point with respect to the origin of coordinates, which in this case is two units and seven units, respectively. Since the segment has been projected on the x axis, we have that the y coordinate of both points is zero.
On the y-axis the opposite is true, the x coordinate is zero while the coordinates corresponding to the end points of the segment, which in this case are 3 and 6 coincide on the y-axis, being the same points.
The dimension of the projected segment is the difference between one point and the other, for example on the y axis is 6 - 3, which is 3. If we subtract inversely we will have 3 - 6, which is -3, the measurement is the same but with opposite sign, for that reason in matter of linear distances what matters is the absolute value, which means that the sign is dispensed with, regardless of whether we subtract one less the other or reciprocally.
in the case of the x axis we have exactly the same, if we subtract 7 - 2 we obtain the distance between the two points that is five, this is the distance on the x axis, subtracting inversely, 2-7 we obtain -5, whose value Absolute is the same, five.
To obtain the distance between two points that are not parallel to the axes, as with points AB whose distance is 5.83, we will have to apply the Pythagorean theorem: the square hypotenuse is equal to the squared leg plus the other leg at square, having therefore that the length of the segment a squared is five (7 - 2) squared plus three (6 - 3) squared.
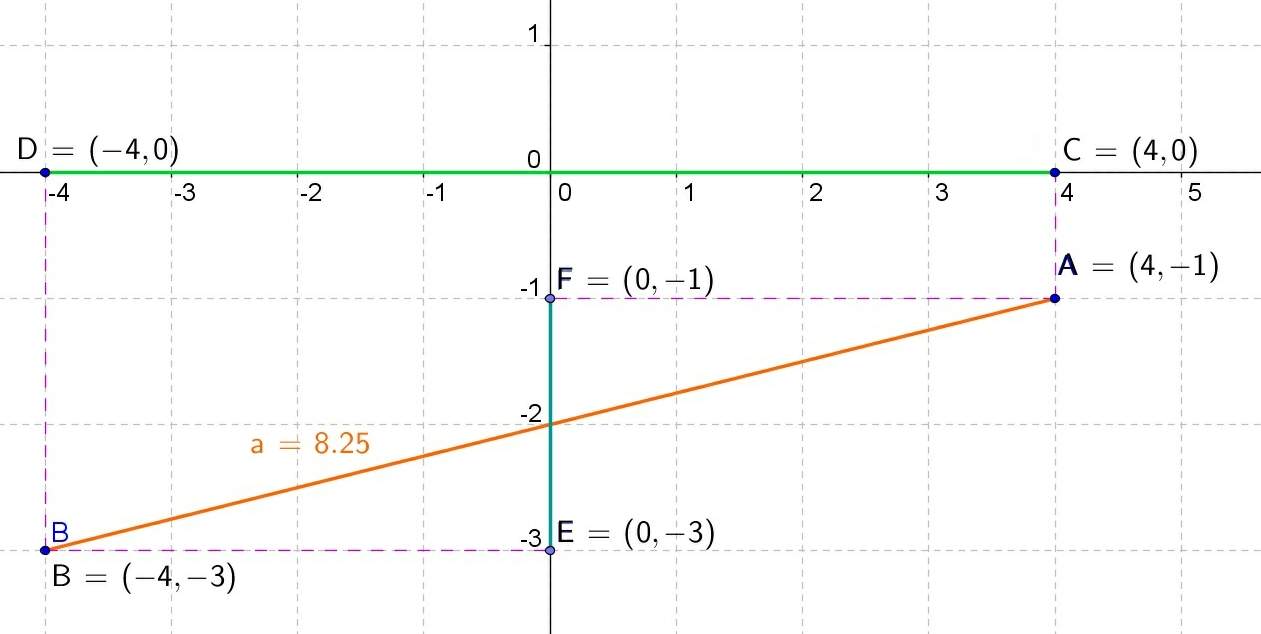
In this case we have the orange segment that is projected on the axis and with coordinates in y -1, -3, while we have to project the points AB on the x axis, we obtain by coordinates in x four, -4.We can observe that both coordinates correspond to those of the points in x and y.
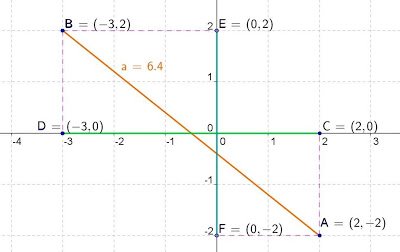
We have again the orange segment of coordinates at its ends (-3.2) and (2, -2).
The coordinates on the x axis (in green) correspond to the coordinates of the points in X, that is, 2 and -3. While the coordinates on the y-axis correspond to those of the points in their coordinates y, that is, -2,2.
Distance between two points
The Cartesian Plane is used as a reference system to locate points in a plane. Another of the utilities of mastering the concepts on the Cartesian Plane is that, from the location of the coordinates of two points it is possible to calculate the distance between they.
When the points are located on the x-axis (of the abscissas) or on a line parallel to this axis, the distance between the points corresponds to the absolute value of the difference of their abscissas (x2 - x1).
When the points are located on the y-axis (of the ordinates) or on a line parallel to this axis, the distance between the points corresponds to the absolute value of the difference of their ordinates. (y1 - y2)
Now, if the points are anywhere in the coordinate system, the distance is determined by the relationship:
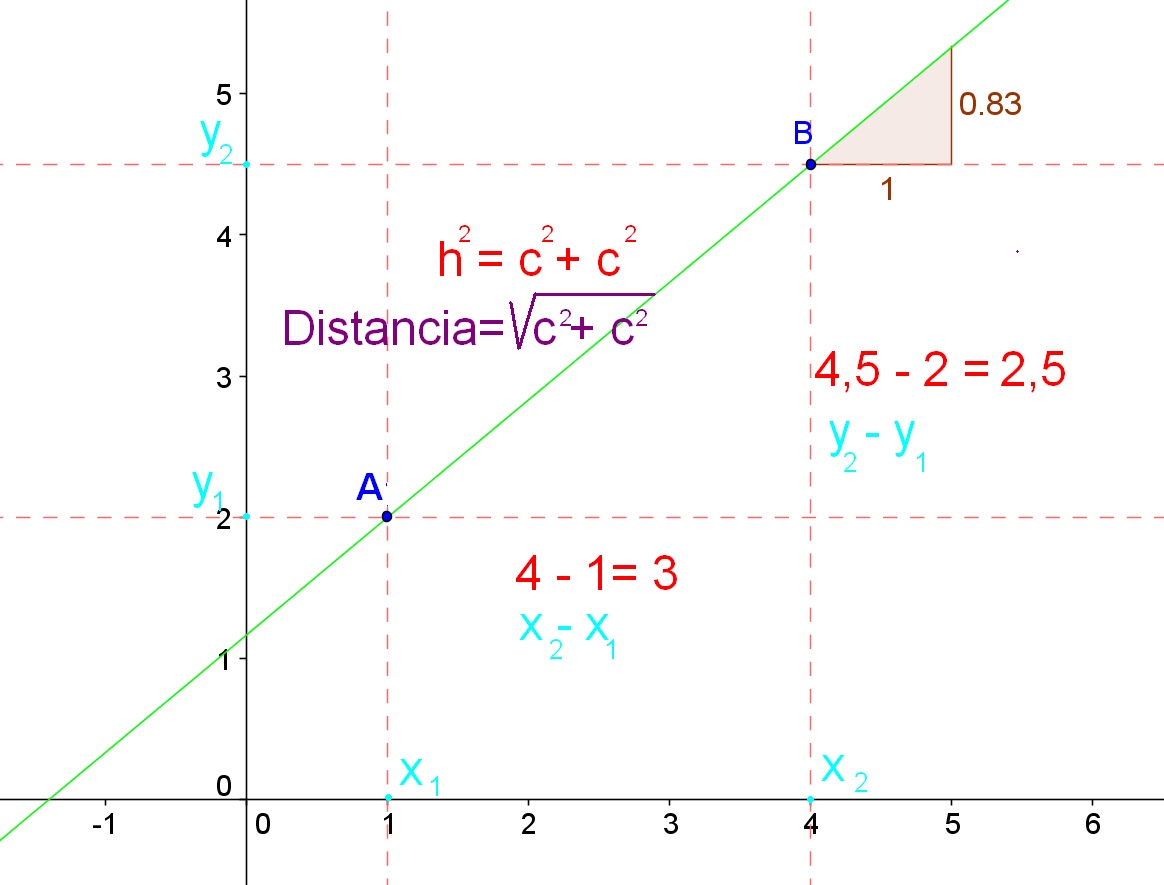
We can observe in the drawing that the projection of segment AB is segment 4-1, we have that the subtraction of both numbers determines the dimension of the segment: Three. Therefore we can say that in any 2 points, the projections of the segment that determine it on the condemned axes are given by the formulas: x = x2-x1
If this construction we have just done, we also do it on the y-axis, we have the segment AB projected on the y-axis and it determines the distance 4,5 minus 2, which is equal to 2.5.
y = y2-y1
Applying the Pythagorean theorem we have that the hypotenuse squared is equal to the sum of the squared squares, consequently if we obtained the dimensions of the projected segments on the Cartesian axes, we can deduce that the distance between any two points of the Cartesian plane is equal to the square root of the coordinate difference in x to the square plus the difference in coordinates in y squared:
Distance between two points = the square root of: (y2-y1) to the square plus (x2-x1) to the square.
Points aligned on a line
Points linearly dependent or aligned
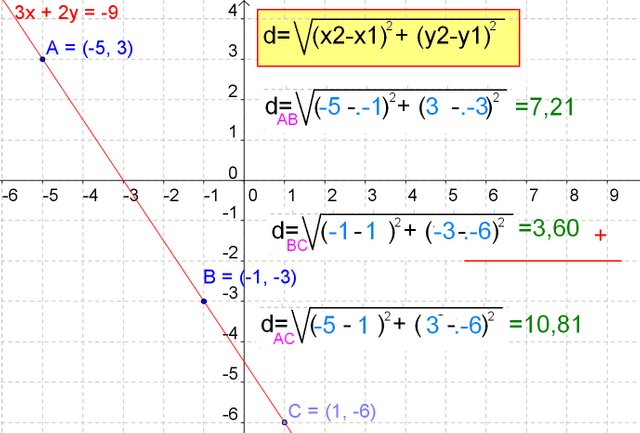
To check if 3 points ABC are aligned and therefore are on a line, we can calculate the distance between two next, for example between points A and B. Next we calculate the distance between B and C, if both distances added determine a number equal to the distance between the ends A and C, this means that the three points are aligned.
If the two distances were not equal, the 3 points would form a triangle, a figure in which the sum of the lengths of two sides is always greater than the length of the other side.
To calculate the distance between any two points, we use the Pythagorean theorem, in which the hypotenuse squared is equal to the squared leg plus the squared leg.
Bibliography :
- Analytical geometry and linear algebra, projection of points. 2016 Sawyer H.Jasson K.
-https://en.wikibooks.org/wiki/Linear_Algebra/Orthogonal_Projection_Onto_a_Line - Analysis of analytical geometry, practical development exercises.2014. Luissanna W. Danci Zaballeta.
-http://www.engineeringdrawing.org/category/projection_of_lines
-http://www.grad.hr/geomteh3d/Monge/03pravac/pravac_eng.html