Mathematical Explanation -Division of polynomial Classes # 1
Hello friends, continuing with my math publications, today I will start a series of publications, related to math classes, where basic concepts of mathematics will be touched and we will also talk about the properties of mathematics, today we begin with the division of polynomials, Now, what we call a polynomial division? Here you can find all the answers of this mathematical property. I invite you to observe this publication.
DIVISION OF POLYNOMIANS
By definition, we know that a polynomial is formed by the addition or subtraction of several monomials. A polynomial can be divided by a monomial or by another polynomial. The operation is very similar to the traditional division of numbers, where there is a divisor, a dividend , a quotient and a remainder. To divide a polynomial is more complex due to the inclusion of algebraic terms that have letters and numbers. Therefore, to explain the division of polynomials.
Exact division of polynomials
In this class we are going to see the division of polynomials.
Consider these two polynomials, one as a dividend D (x), and another as a divisor d (x)
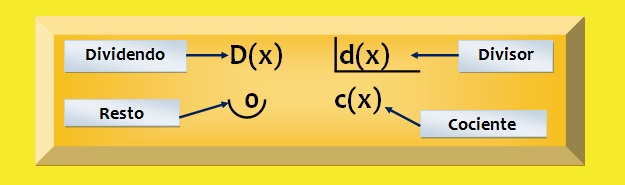
In an exact division of polynomials, the rest is equal to zero.
To divide the polynomial D (x) between the polynomial d (x) is to find another quotient polynomial c (x) such that multiplied by the divisor gives the dividend:
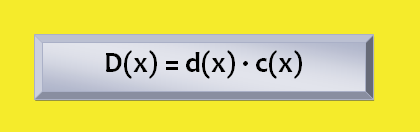
In this case it is said that the division is exact and it is said that the dividend D (x) is a multiple of the divisor d (x) and the quotient c (x). It is also said that d (x) and c (x) are divisions of the polynomial D (x).
Whole division of polynomials
Consider these two polynomials, one as a dividend D (x), and another as a divisor d (x):
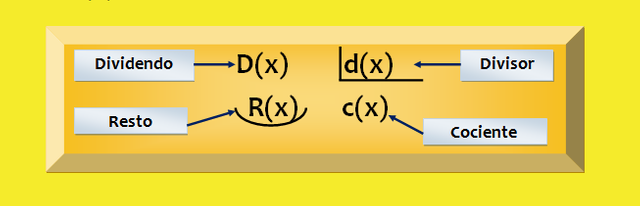
In a whole division of polynomials, the rest is nonzero.
In the whole (or inaccurate) divisions, the dividend D (x) is not a multiple of the divisor d (x), and the fundamental property of the division will always be fulfilled:
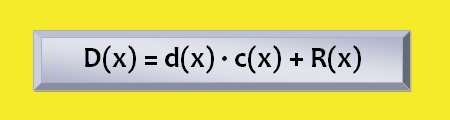
The degree of the polynomial remainder R (x) is always smaller than the degree of the divisor polynomial d (x).

Division of a polynomial by a monomial
To divide a polynomial by a monomial, each monomial of the polynomial is divided by the monomial, until the degree of the dividend is less than the degree of the divisor.
To verify that the division is well done, we look if the fundamental property of the division is met:

In our example:
D (x) = 2x² + x - 2 ⇒ Degree of D (x) = 2
d (x) = x ⇒ Degree of d (x) = 1
c (x) = 2x + 1 ⇒ Degree of c (x) = 2 - 1 = 1
Division of a polynomial by another polynomial
Consider these two polynomials:
To carry out the division of D (x) between d (x), proceed as follows:
1 . The polynomials are placed as in the division of numbers and ordered in an increasing way.
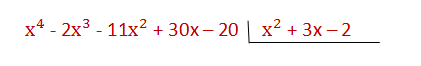
2 . The first monomial of the dividend is divided by the first monomial of the divisor. The result is put in the quotient.
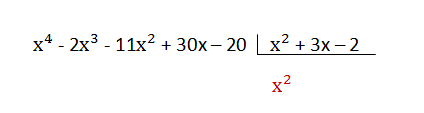
3 . The quotient is multiplied by the divisor and the product obtained is subtracted from the dividend:
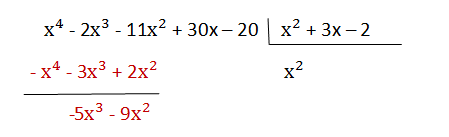
4 . The following term is lowered, 30x, and it is divided, as in section 2, the first monomial of the dividend (-5x³) by the first monomial of the divisor (x²)
and it is placed -5x in the quotient
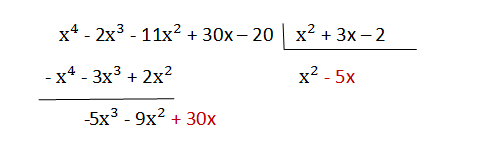
5 . Multiply -5x by the divisor (x² + 3x - 2) and the product obtained is subtracted from the dividend:
Since we have to subtract -5x³ - 15x² + 10x from the dividend, we add the opposite:
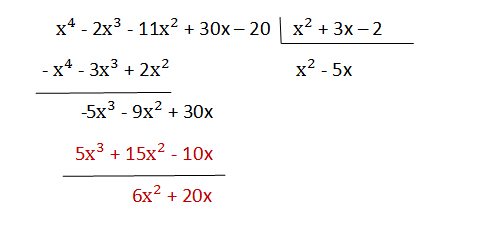
6 . The last term, -20, is lowered, and the first monomial of the dividend (6x2) is divided, like sections 2 and 4, by the first monomial of the divisor (x²)
6x² ÷ x² = 6, and 6 is placed in the quotient
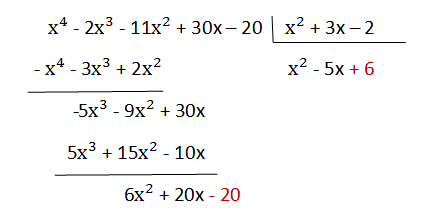
Bibliogaphy :
- https://en.wikipedia.org/wiki/Polynomial_long_division
- https://en.wikipedia.org/wiki/Polynomial_long_division
- http://www.webmath.com/polydiv.html
- https://www.mathsisfun.com/algebra/polynomials-division-long.html
- http://www.mesacc.edu/~scotz47781/mat120/notes/divide_poly/long_division/long_division.html