深度学习笔记 III – 卷积神经网络的直观解释 C - Introducing Non Linearity & Fully Connected

#1 深度学习笔记 I – 卷积神经网络的直观解释 A - 整体结构
#2 深度学习笔记 II – 卷积神经网络的直观解释 B - Convolution & Pooling Step

这一篇用于记录卷积神经网络中另两个主要的操作Non Linearity and Classification（Fully Connected Layer），加上#2中的Convolution and Pooling step, 这四个操作构成了所有卷积神经网络的最基本结构模块。

添加非线性因素（Introducing Non Linearity (ReLU)）

这一步其实是在卷积操作之后，Pooling操作之前的。但还没有搞明白这一步背后的数学原理，所以在上一篇没有记录，这一步还需要学习，会在后面的笔记中专门记录一篇。目前的理解是这一步是为了添加非线性因素，因为卷积神经网络要学习的真实数据都是非线性的，而卷积操作是乘法和加法的线性操作。添加非线性因素的这一步用到了叫做激活函数的概念，这里记录的是ReLU激活函数（为什么叫激活函数？），还有另两个使用概率高的激活函数是tanh or sigmoid，但ReLU据说已经被证实在大多数情况下要比另两种的表现更好。（翻译成激活函数，不要误解是指这个函数去激活什么，而是指如何把“激活的神经元的特征”通过函数把特征保留并映射出来，这是神经网络能解决非线性问题关键）

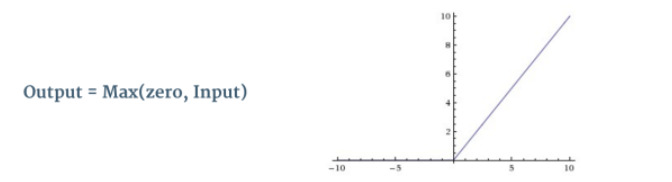
ReLU是Rectified Linear Unit的缩写，函数表达式很简单，就是小于零的部分，取零，大于零的部分不变。

下图很好的说明了ReLU操作的结果，左边是卷积操作过后得到的特征图，经过ReLU操作后，得到右边的图中的像素值全部都是大于零的值。

Image source [1]

等一等（Story so far）

回顾一下目前记录的三个操作步骤，卷积->引入非线性元素->Pooling，这三步都是任何卷积神经网络的基本操作步骤。下图中，展示了两套这样的三步操作，第二次卷积的输入值是上一套卷积->引入非线性元素->Pooling操作的输出值。这两套卷积->引入非线性元素->Pooling操作不同的时候，第二套中有6个过滤器（Filter），其余的卷积和Max Pooling都是一样的。

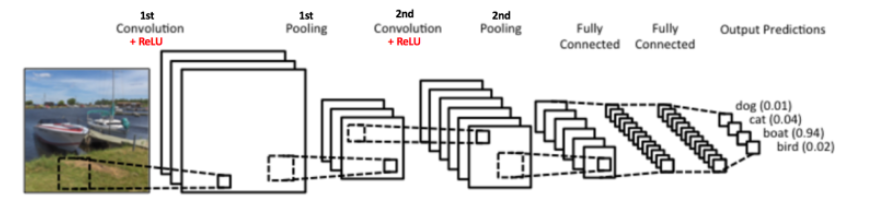
Together these layers extract the useful features from the images, introduce non-linearity in our network and reduce feature dimension while aiming to make the features somewhat equivariant to scale and translation. [2]

全连接层（Fully Connected Layer）

上图中在第二组卷积->引入非线性元素->Pooling操作之后得到结果被作为输入值送给全连接层。该层的主要作用就是连接特征图到传统的多层感知器（这个多层感知器需要接下来单独一篇记录，这篇文章讲的不错）。全连接的意思就是在前一层的神经元连接到下一层中的每一个神经元。卷积层和Pooling层的输出代表了输入图像的高级特征， 全连接层的目的是使用这些高级特征将输入的图像分类为基于训练数据集的各种类别（例如猫，狗，汽车，人等等）。
例如下图中的全连接层就是将输入图像的特征图归纳为四中可能的类别，并且给出可能性大小的值。从图中可以看到船的类别的可能性最大，所以输入图像应该是一艘船（这里的记录顺序不够好，应该先记录一下多层感知器，没有多层感知器的知识，这一步全连接很唐突，后面的文章补上）。

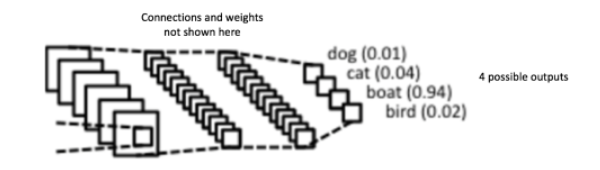
所有结果的可能性的总和应该为1（这里为什么是1.01？），这是由于应用了Softmax as the activation function在全连接层的输出层中（Softmax函数的功能其实就是全相加再做除法，得到各个值的比重）。

Apart from classification, adding a fully-connected layer is also a (usually) cheap way of learning non-linear combinations of these features. Most of the features from convolutional and pooling layers may be good for the classification task, but combinations of those features might be even better [3].

是时候把它们全都搞到一起开始学习训练了（Putting it all together – Training using Backpropagation）

之前这些所有的步骤，卷积和Pooling可以看作是特征获取者；全连接层可以看作是分类者。可以开始看看训练是怎么回事了。如下图所示，输入图像是船，所以全连接层的输出结果应该是[0 0 1 0]。所以要训练这个网络，

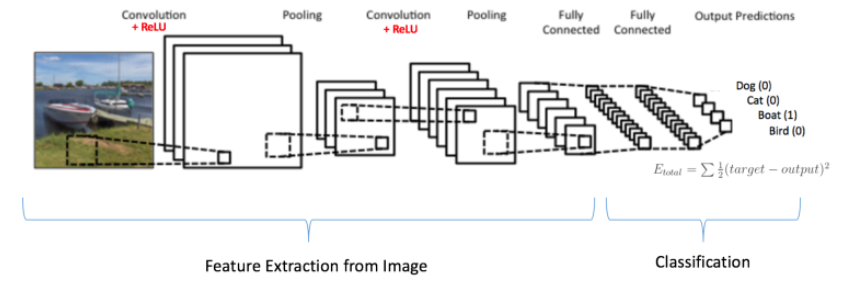
整体的训练学习可以总结为以下几步：
第一步：初始化所有的过滤器和参数，以及权重值。
第二步：选择一个训练图片，经过正向的神经网络操作（卷积，Pooling，全连接），得到一组不同类的可能性的值,因为权重值都是随机赋予的在第一步中，所以得到值也是随机的，例如结果是[0.1 0.5 0.3 0.1]。
第三步：计算误差。
第四步：利用反向传播去调整过滤器中的数值以及全相连层中的权重值，其中权重的调整是根据它们对最终误差的影响大小做调整的。当调整到输出结果可以判定输入图像的分类时（例如[0.1 0.1 0.7 0.1]），学习过程结束（这里需要单独一篇记录一下如何做调整的）。

When a new (unseen) image is input into the ConvNet, the network would go through the forward propagation step and output a probability for each class (for a new image, the output probabilities are calculated using the weights which have been optimized to correctly classify all the previous training examples). If our training set is large enough, the network will (hopefully) generalize well to new images and classify them into correct categories.

我记录的笔记，完全把卷积神经网络过度简单化了，也没有谈任何这其中的数学原理。如果想学习这其中的数学背景的可以阅读这篇文章：Convolutional Neural Networks:Math->Code。我是学工程的，是为了应用卷积神经网络，哎，导师要求月底前搞明白caffe，可是今天离caffe的距离还是好远。

Note* 卷积神经网络中并不一定非要卷积，添加非线性，Pooling这样的操作一套接一套重复好几遍。也可以卷积好几遍，然后接一次添加非线性和Pooling。

玩起来，即使你根本不打算知道卷积神经网络是什么 （Let's Play!!!）

Adam Harley开发了一个让你可视的神经网络模型用来让你看到神经网络是如何识别单个数字的，非常炫！强烈建议进去玩一下，即使你不打算和神经网络有交集，只需要你用鼠标手写输入一个数字，整个神经网络的各个层全都显示出来了。

Adam Harley created amazing visualizations of a Convolutional Neural Network,I highly recommend playing around with it to understand details of how a CNN works.

下图中就显示了卷积神经网络是如何识别数字6的，因为空间有限的原因，添加非线性的操作没有单独列出来。

第一步卷积操作，5X5的过滤器在32X32的输入图片中以步幅1滑动，可以看到这里有6个过滤器，说明depth的值是6（与要识别的数字6纯属巧合）。

Max Pooling操作，2X2的小矩阵在卷积结果上取最大值（越亮的像素块的值越大），得到Pooling后的结果。

这下直观的看到了什么叫全相连了吧（前一层的神经元与后面一层的每一个神经元都相连），最后最亮的点就是数字6，说明输入的数字被识别为是6的可能性最大。

可以尝试一下写一个你认为不好识别的数字，看看结果如何：D

This post was originally inspired from An Intuitive Explanation of Convolutional Neural Networks by Ujjwalkarn, I got the permission from original author by e-mail let me use it. All images and animations used in this post belong to their respective authors as listed in References section below.

在这个秋天，为自己的学习过程记录。

Reference
[1] http://mlss.tuebingen.mpg.de/2015/slides/fergus/Fergus_1.pdf
[2] https://github.com/rasbt/python-machine-learning-book/blob/master/faq/difference-deep-and-normal-learning.md
[3] https://stats.stackexchange.com/questions/182102/what-do-the-fully-connected-layers-do-in-cnns/182122#182122

---

谢谢阅读 !

Please feel free to upvote, comment and follow me @victory622

---