Vibration - physics explained
It is time for some fun science again! I have been thinking about what this post will be for the last two days. The first idea was to write about sound and then I realized how that topic is really huge and a post about it would be just too long. I realized that before sound I should explain waves first and in my next lesson move on to sound. That was all fine but there is no understanding of waves without vibration and periodic movement first. So, the vibration it is. Before we start, here is a list of previously published posts in my series Physics explained:
DOPPLER EFFECT
COLD BOILING WATER
HOW DO WE SEE COLORS
LEARN ABOUT RAINBOWS
EVERYTHING IS MAGNETIC!
NEWTON'S LAWS OF MOTION
DIFFERENCE BETWEEN HEAT AND TEMPERATURE
CALCULATE THE SPEED OF LIGHT USING CHOCOLATE
To follow along this post, no previous knowledge of physics is necessary, however, this post will be needed to understand those that will follow it so think about this as lesson 1, waves as lesson 2 and then finally, sound as the lesson 3. Enjoy the post and feel free to contact me if you have any questions or want to know more. Are you ready to learn about vibration? Let's go!



When things vibrate, they move back and forth from their equilibrium position. That is the same position in which an object would be if it was not moving at all, the position where the net force on that object is zero. So, if we have an object that can vibrate and we apply an external force on it to disturb that state of equilibrium, it will start moving away from the equilibrium, stop at some point and come back to equilibrium, pass it and move to the other side, then stop and come back and so on and so on...

We see vibration everywhere in our daily lives. From bobblehead dolls in our cars, pendulum clocks, balls bouncing off walls or floors, children on swings, trees swinging in the wind or any other motion of shaking and swinging. There is usually elastic thing involved or a one that is hanging from something like a pendulum. These are all examples that we can see but if we go deeper we will find that in fact, everything vibrates, even solid objects that seem like they are still. In solids, particles are vibrating too and only at the temperature of absolute zero (-273 °C) all movement stops. Since I have covered electrons in my previous posts, we will stick to macrophysics this time and discuss vibration and periodic motion that we can clearly see.

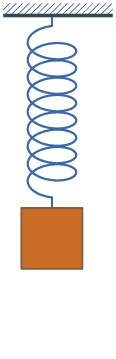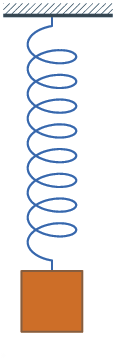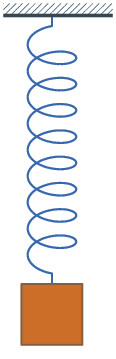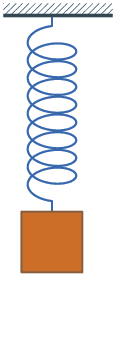
When vibrations are regular and repeated, we categorize them as periodic. An object moves over the same path over the course of time and the motion repeats itself until the damping stops it. Mass on a spring and pendulums are the best examples to learn about periodic motion so let's see the mass on a spring. It is in the gif right from this text.
Look at that animation and pick a starting position the mass is in. To be on the same page with this, let's start with mass being at the bottom. From there, it will go up to equilibrium, pass it and continue going up where it will stop and change direction and start coming back. On its way back it will again pass the equilibrium and come back to the bottom. We call this a cycle and it is always made of 4 parts. If we started from the equilibrium and the mass went up, the cycle would not be when it first came back but the second time. The mass goes from equilibrium up, comes back, passes it, goes down and then comes back to equilibrium.
Time for the mass to complete a cycle is called PERIOD
Since time is measured in seconds, units for the period are also seconds and we use the capital letter T as its symbol. If we turn that definition around and ask ourselves how many cycles take place in a period of time then we have a frequency. We label frequency with f and measure it in Herz. Here is the relation between period and frequency:
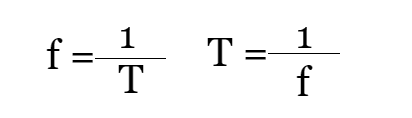
They have a reciprocal relationship. A period is a time for one full cycle to complete itself and a frequency is the number of cycles that are completed per time. We can easily get one from the other so to define any periodic motion we need only one of them. The other thing that is often mentioned in periodic motion is amplitude. Remember when I told you to imagine a mass starting from the bottom position? That is amplitude. The symbol we use is capital letter A and as any other distance, we measure it in meters.
The amplitude is the maximum displacement
of an object from its equilibrium position


Since we already said some basic things about the mass on a spring, this is a good time to introduce ourselves to the simple harmonic oscillator. It consists of a weight attached to one end of a spring while the other end is connected to a rigid support. When the system is left at rest at the equilibrium position then net force acting on the mass is zero. If the mass is displaced from the equilibrium position, the spring exerts a restoring elastic force that obeys Hooke's law.
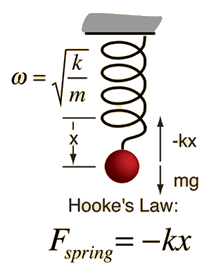
Hooke's law states how the force (F) needed to extend or compress a spring by distance x scales linearly with respect to that distance. That force always has the opposite direction from the movement and displacement x because when the spring is compressed, the force wants to extend it and when it is extended, it wants to compress it. The force tends to restore the system to equilibrium. This is the explanation for the minus sign in the formula: F = −kx
F (in Newtons) in that formula is the restoring force, x is the displacement (in meters) and the k is the spring constant (N·m−1) that depends on the material from which the spring is made of.
Let's see the entire motion
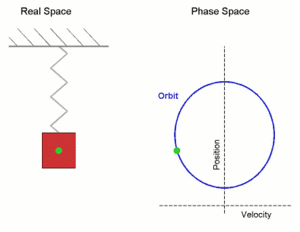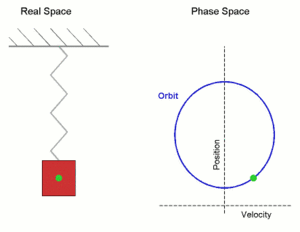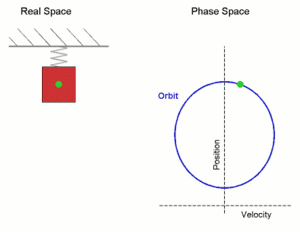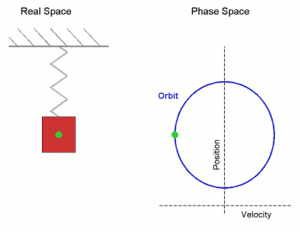
When we put a mass on a spring and the system is at rest, the mass is at the equilibrium position. The net force is zero because the force of the spring is equal to mg that is pulling the mass towards the ground. When we displace the mass from its equilibrium position and let it go, it experiences a net restoring force. The mass moves towards the equilibrium position. The closer the mass gets to equilibrium the smaller the restoring force is until it becomes zero in the equilibrium position. The acceleration is zero before the mass started to move from the bottom but it is the highest as soon as we let it go and that is the starting point of this movement. The acceleration is decreasing the closer the mass gets to the equilibrium where its value is zero.
At the equilibrium, the mass has momentum and it continues to move up while the spring compresses. As the spring is compressing the acceleration is increasing. The restoring force is slowing the mass down until it stops at the amplitude position where the acceleration reaches its highest value again and the mass starts moving back down while the acceleration decreases again until it reaches zero value at the equilibrium again. When the mass passes the equilibrium it starts to slow down until it reaches the bottom amplitude from where it started. If there is no energy loss, this movement will repeat itself and we have a simple harmonic oscillator with harmonic motion. Since there is an energy loss because of damping, the amplitude will shorten more and more with time until it finally becomes zero and the movement stops.
What about energy?
If you remember that a body has potential energy when it is at rest and kinetic energy when it has speed, you will easily comprehend what happens with energy in this motion that we described. Let us look at the graph.
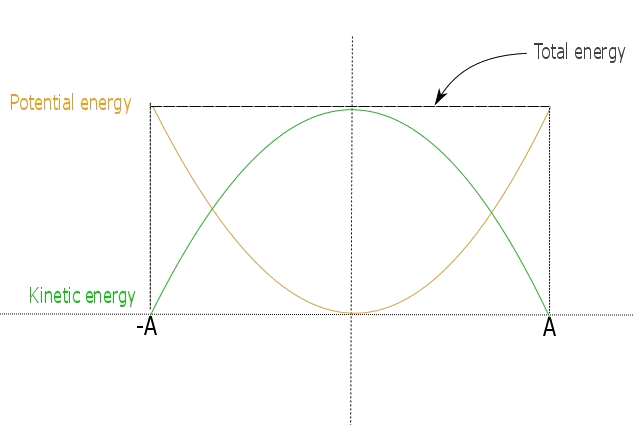
Keep in mind that the total energy is always the sum of kinetic and potential energies. We started in the amplitude position where the body is at rest before we have let it go. Since it is at rest, there is no kinetic energy and the entire energy is potential. When the body starts moving, its potential energy decreases and the kinetic one increases as it is picking more and more speed. In the equilibrium position, the potential energy is zero and the entire energy is kinetic. When the body continues to move to upper amplitude, that kinetic energy is decreasing and the potential one increasing until the position of amplitude where there is again no kinetic and the entire energy is potential. I think it is time for a review of what we have covered so far...
| Position | Energy | Acceleration | Force | Speed |
|---|---|---|---|---|
| Lower amplitude | POTENTIAL | maximum | maximum | zero |
| Equilibrium | KINETIC | zero | zero | maximum |
| Upper amplitude | POTENTIAL | maximum | maximum | zero |
As you can see, displacement, speed, and acceleration are periodic. We can solve differential equations to get solution functions. Those functions are trigonometric. If this is too much for you, I won't mind if you scroll through this part. :)
| Physical quantity | Solution function |
|---|---|
| displacement | x = cos(ωt) |
| speed | v = -Aωsin(ωt) |
| acceleration | a = -Aωωcos(ωt) |
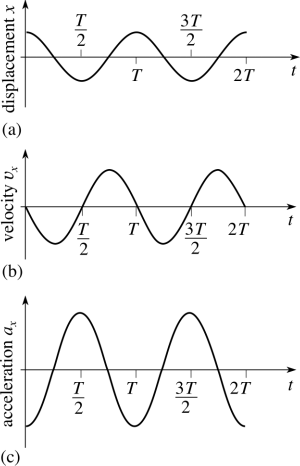
Those are solutions to differential equations and ω = 2πf is the angular frequency. We can see the graphs of those function and notice how everything can be explained just by looking at them.
As you can see from these graphs, displacement starts from amplitude, velocity from zero because it is zero there and acceleration from its maximum value. Functions are periodical and they change in a way that we already explained.
We are now moving to an important question regarding the period and the frequency. What do they depend on? Will the movement change if we change the mass or will it change if we have the same mass but increase the amplitude?
The period and frequency are independent of the amplitude
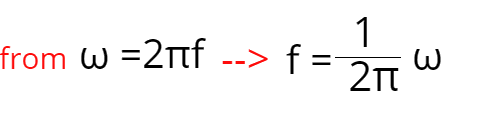
It does not matter if you pull that mass down by just a couple of centimeters or by a meter, the period and the frequency will be the same. Let's see why that is. We know that angular momentum is ω = 2πf and we also know that angular moment depends on mass and the spring constant which is shown with these formulas:
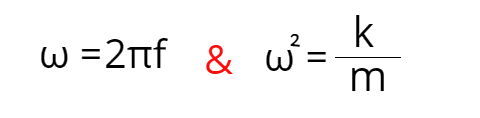
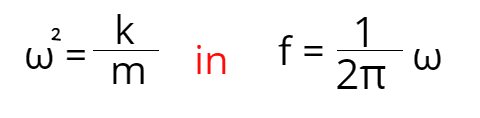
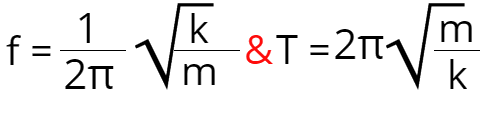


As I said in the beginning, to get to sound we first need to discuss waves and to start talking about waves we needed vibration. In this physics explained post we have covered vibration and everything we will need regarding harmonic motion from displacement and acceleration to energies and frequency. Be patient, waves are coming soon, are you ready for them? Until next time
KEEP YOUR SMILE ON
RESPECT YOUR INNER GENIOUS!

To learn more about this topic, be sure to check out these resources:
Simple harmonic motion
Vibrational motion
Vibration
Periodic motion
Hooke's law
Harmonic motion
If you are interested in something physics (or science in general) related, tell me and I would be happy to make a post about it and explained it. Promoting science and making it understandable gives me great joy, I would be happy to help you.

Image sources:
- gif image of mass on a spring is from wiki and can be found here
- cover image is from pngtree and is royality free, it can be found here
- clipart in my titles is from pixabay and is here
- red mass on spring is from hyperphysics.phy and is here
- real space and phase space gif is from wiki and is here
- graph with energies is from Periodic Motion. Brilliant.org. Retrieved 08:25, July 25, 2018, from https://brilliant.org/wiki/identifying-periodic-motion/
- 3 graphs are from physics.brocku and are here
- pendulum clock is from wiki and is here
- all the other images with equations I made myself
- cover image is from pngtree and is royality free, it can be found here
- clipart in my titles is from pixabay and is here
- red mass on spring is from hyperphysics.phy and is here
- real space and phase space gif is from wiki and is here
- graph with energies is from Periodic Motion. Brilliant.org. Retrieved 08:25, July 25, 2018, from https://brilliant.org/wiki/identifying-periodic-motion/
- 3 graphs are from physics.brocku and are here
- pendulum clock is from wiki and is here
- all the other images with equations I made myself
PROUD MEMBER OF:



@steemitbloggers

Learned this in my schools but now learning a new kind of wave.Wave of probability in quantum mechanics and it's really great.
Probability is always an interesting subject, I am glad you find it interesting.
At first it is hard to digest but after that it becomes the most interesting topic
It's been a fair while since I thought of amplitude and frequency both at the same time. I got my 2nd class radio engineers ticket about 48 years ago. I learned a lot of things there that I didn't need at the time but all knowledge will be useful in it's time. Thanks for making it time!
It seems to me that all you would have to do to end this series would be explain Gravity Waves in your patient and thorough style to win the Nobel. You can do it, I think.
Thank you for another great thought provoking post. I really enjoyed it.
OH WOW!!! Me explaining gravity? LOL, honey you give me too much credit and overestimate my abilities. It is cute and I am very lucky to have such a passionate encourager like you. Thank you very much 💚
Wow you took me back to school!! Look at you! You have been busy with your Physics series! I love the idea how you are breaking down these aspects and defining what they are. I love the graphics and animations you used to help us get the “picture”! 😄 Thank you for such a thorough outline of vibration
I am so happy when I get a comment like this, thank you honey! I am very glad you enjoyed this 💚
Absolutely! 😉
This took me back to lessons with my physics tutor, a long long LONG time ago! I have a vague feeling that friction came into the equation eventually... it was friction that disturbed the perfect equilibrium of the vibration cycle. I'm not sure if I've got that right, but brilliantly explained once again!
Yeah, friction always comes and screws things up :D Thank you for your lovely comment 💚
The question should be asked, though, based on the fact that "equilibrium position" is, however convenient, a complete delusion-there is an intrinsic frame of roughly constant acceleration, not limited to 4d, but some higher ordinality.
Does motion affect other parameters of a body than positional only?
To basic physics, it doesn't, but empirical evidence continues to mount disproving that in very subtle and startlingly obvious ways.
That would be a wonderful topic for a post, that I haven't more than a few brief moments to spend to develop, but perhaps someone else might be able to spend the time.
OF course simplified newtonian physics does not always include all of the subtle nuances, but I am having trouble understanding the higher ordinality needed with a sine wave. Of course the equilibrium position is a convenient concept in a frictionless environment, but my experience here on Earth is that things eventually stop and settle just so in the middle.
I would read the article you alluded to here though, with gusto!
We do not live in the frictionless environment, there is always a certain amount of damping. Maybe I should have gone further and introduced full equations that do include friction but I was worried it would scare people off :) I am, however, very satisfied with so far reactions and how well received this post is concerning the fact that the majority of my readers are not familiar with the subject. On the other hand, this text is veeeeery simple and not at all explained enough (in my opinion) to satisfy the needs of those with a scientific background or understanding. I am still finding the balance to satisfy both sides :) Thank you for your lovely responses and inputs, they will be taken into consideration and are very much appreciated. 💚💚💚
That's a very good approach and I like to keep it simple as well. I also like comments that clear the things for everyone. You are doing a great job!
Hey @zen-art
Here's a tip for your valuable feedback! @Utopian-io loves and incentivises informative comments.
Contributing on Utopian
Learn how to contribute on our website.
Want to chat? Join us on Discord https://discord.gg/h52nFrV.
Vote for Utopian Witness!
Thank you for those motivating green hearts!
I feel like being on steem with people like you makes me smarter and happier :)
DId you understand @tvulgaris' question? I thought that he was saying that there is no equilibrium, and I think that things do actually arrive to equilibrium as long as we include friction. Also, as you listed on your charts, the equilibrium is at the point where velocity is maximum.
This post was shared in the Curation Collective Discord community for curators, and upvoted and resteemed by the @c-squared community account after manual review.
Thank you very much deer C-squared people 💚💚💚
I feel like I have learned something today by stopping in, thanks for lesson. Look forwards to part two of this section.
I am glad you stopped by and that you found this interesting, I am sure the waves will be even better to read about. Thank you for your feedback 💚
I had always heard that every single thing on earth has a resonance frequency that is determined by the vibration of the object. The waves are the form it takes when measuring with a scope. That is how a singer can shatter glass with their voice, by changing the vibration of the glass by filling the air with a sound vibration that acts on the glass.
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by zen-art 💚 from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, theprophet0, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Thank you! I am glad that you found this post valuable and your support is very much appreciated 💚
Hi @zen-art!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Thank you! Your support is very much appreciated!!! 💚💚💚