Blockchain Decrypted - How mining works
Credit
To be very clear, the below is largely based on Azotic’s post on Reddit from February 2013 (https://www.reddit.com/user/azotic); he/she provided such a great explanation that I didn’t see the point in rewriting a lot of it. This chapter is purely here for reference in later chapters.
Introduction
Blockchain “proof-of-work” mining usually comes with a statement that miners “solve a difficult math problem” or miners “guess for the answer” and while both are true, neither are accurate; other times the answer given is too arcane, talking about such-and-such hash function this, algebraically that, Merkle trees and branches and leafs, etc.
This is aimed at being a non-technical explanation, to simplify mining and introduce the concept to people unfamiliar with it.
Blockchain Mining
It’s not really about computers solving complex mathematical problems, it is more about computers taking structured guesses at a rapid pace to solve the mathematical equation. While the end result is indeed a solution, the way of getting to the solution is not by solving it but by running a growing sequence of numbers until you arrive at the solution. I.e. actual intelligence is not required to mine. That is also the reason why GPU and ASIC mining have replaced CPU mining.
Hash Functions
To start to understand mining, you have to understand what a hash function is and that there are a variety of predetermined hash combinations in the whole blockchain story.
A hash function takes an input and creates a seemingly random output; important to note here is that while the output is randomized it is consistent, I.e. every time you enter the exact same input you will receive the exact same output. Aside from this, it is very difficult (astronomical) to determine an input if you only have the output.
An example of a very simple hash function using prime numbers:
a. Using a calculator, take the square root of 3, this will give you 1.7320508075887729352744634150
b. Now take the digits from the 5th place after the decimal all the way to the 10th place after the decimal, this gives you 508075
c. Try this again with another prime number, for example, 11, this will give you 3.3166247903553998491149327366707
d. Again, take the digits from the 5th place after the decimal all the way to the 10th place after the decimal, this gives you 247903
e. That is, in its simplest form, a hash function, all be it a very weak one.
f. For any given prime number, we can find a number, (those 6 digits from 5-10: 508075) that seem to have nothing to do with the input (the square root of 3) but that can be consistently calculated and that cannot be easily reconstructed to give you the input.
g. If I give you the number 512754, what would the input be?
h. You can guess it by starting to calculate the different square roots of prime numbers, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, etc. and looking at the 5th to 10th numbers in their sequence and compare it to the number 512754
i. You would find it when you hit the number 13 … congratulations, if you did the calculations, you just became a miner.
So how does it work in Bitcoin for example?
a. In Bitcoin they use a hash function called SHA-256, meaning a Secure Hash Algorithm (SHA) that is 256 bits, this belongs to the SHA-2 family which consists of 6 different hash functions. SHA-256 is a hash function that is computed with 32-bit words.
b. This function can use any text (minimum zero characters) and convert that into a cryptographic hash.
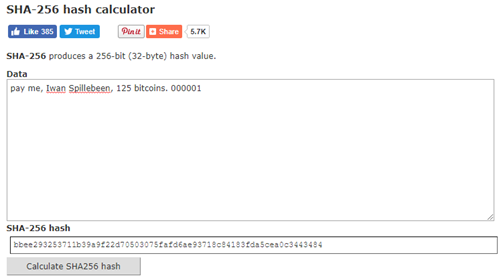
c. A visual example:
c i. In a SHA-256 Hash calculator, type the following text (without the quotes): “pay me, Iwan Spillebeen, 125 bitcoins. 000001” and then press calculate. You can find one at the following link: http://www.xorbin.com/tools/sha256-hash-calculatorc ii. You will receive the following cryptographic hash: bbee293253711b39a9f22d70503075fafd6ae93718c84183fda5cea0c3443484
c iii. As you can see, it would be virtually impossible to derive the text: “pay me, Iwan Spillebeen, 125 bitcoins. 000001” from the hash: bbee293… yet anytime someone puts that exact same text into a hash generator they will receive the hash as an outcome (provided they match the text exactly).
Proof-of-Work (PoW)
So why would you get bitcoins or other cryptocurrency coins for doing that? The answer is simple, you don’t. Cryptocurrencies such as Bitcoin reward miners based on a concept of Proof-of-Work (PoW).
a. The miner needs to prove that they have done work “mining” the block, this is done by assigning a predetermined (changeable) output to the hash of a block. I.e. if you take a block and you take all the hashes of the transactions and the hash of the previous block and the date / timestamp of the block, you will receive a hash for this block. In cryptocurrencies this hash however needs to comply with certain conditions, the hash of a block needs to start with a zero (or a number of zeros). So miners start adding numbers to the block in a predetermined field (the nonce) and recalculate the hash of the block until the hash of the block starts with a zero (or a number of zeros).
b. The nonce in a Bitcoin block is simply a 32-bit (4-byte) field whose numerical value is set so that the hash of the block will contain a run of leading zeros.
c. You can do the same in my example by gradually increasing the number from 000001 to 000002 and recalculating the hash until you receive a hash with a zero in front. You’ll need to do so 17 times to get to the first hash starting with a zero: 0169ab403000e060e708a6e51d139eb0421c9d27f872b726f40d01049de75efd
e. Per the example above, as soon as you get to 000017 the hash starts with a zero: 0169ab403…. so there is now proof of work, I.e. 17 attempts to get to a hash starting with zero. I can share this with the network and get this easily validated.
f. Obviously miners don’t use a “pay me, Iwan, …” text but transactions and other data but this is the core principle of mining.
g. Since nobody knows up front how to take a given output to create a given input with this hash function, we can prove that it took some work to get to an output that starts with a zero. Obviously computers can calculate this at breakneck speed rather than clicking on a generate button, that is why currently (11/01/2018) bitcoin hash outputs for blocks start with 18 zeros in order to be accepted by the network as a solution.
h. Also important to note is that the nonce isn’t just sequential, it is different for every block, as it depends on the hash of the block, which comprises of all the elements in the block. Below an example of actual Bitcoin blocks mined:


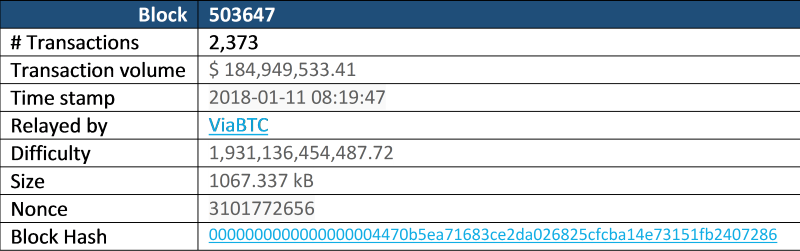
i. You can see from this example that the Nonce for the latest block (503647) was 3101772656, whereas the nonce for block 503646 was 366664386 and the nonce for block 503645 was 190677343. The difficulty for each block was the same however.
j. You can also see that the size of the block and the number of transactions or even the transaction volume have no influence on the mining difficulty of the block in question.
k. There are a number of other interesting items you can learn from this block summary but we’ll talk about that later.
l. You can find the details of each block on the blockchain:
503645: https://blockchain.info/block/0000000000000000000818f1680aef2ccbe6efc003975e7ec0ea0f5465ed9dbc
503646: https://blockchain.info/block/000000000000000000246276d70a63fb0f3adc8f94a8516361310543f170ef63
503647: https://blockchain.info/block/0000000000000000004470b5ea71683ce2da026825cfcba14e73151fb2407286
Network Validation
So how does the network validate your proof of work as a miner and therefore agree that you should get the shiny newly minted bitcoins?
a. They do this quite easily and quickly by simply looking at the block you’ve created, and all the data in it (transactions, hashes, previous block hash, date / time stamp, etc) and by checking your input (transactions) and output (starting with 18 zeros) and calculating this output by generating the hash of the block, adding the nonce and receiving the same answer as you gave them.
b. Provided your time stamp is the earliest one to find the solution, once one computer validates your solution, it broadcasts this validation again to the rest of the network, they validate, etcetera, until the entire network (51%) agrees and thus honour your address with the newly minted coins. This is all captured in that same block, in the Coinbase Transaction section of the block in question, which doesn’t have an input or from addresses.
c. You can see this when looking at the block on Blockchain.info, the first transaction in the list is the allocation of coins, it states: “No Inputs” and “Unable to decode output address”.
Changing the difficulty
We’ve seen how to do proof of work, how to mine and what the nonce is. So how is the difficulty determined?
The difficulty is determined by the number of zeros you need to start the block hash, this difficulty is adjusted every 2,016 blocks. This adjustment can be up (more difficult) or down (less difficult) and completely depends on the “hash rate” of the network over time.
The “hash rate” is the total power of the network trying to find solutions to blocks, currently this is at about 16,000,000 terra hashes per second (yep, 16 million trillion hashes per second): https://blockchain.info/charts/hash-rate (date of posting 11/01/2018) at a difficulty of 18 zeros.
A solution is found approximately every 10 minutes for one block, this is artificially kept at this 10 minutes time frame, and the difficulty is adjusted up or down to stick to this 10 minute time frame in Bitcoin. Ethereum for example allows blocks to be mined every few seconds.
The difficulty setting is determined by the Bitcoin users (yes the users) not on a consensus basis; each bitcoin user calculates the difficulty of the solutions that they will accept and relay this information to other nodes on the network.
That doesn’t mean that different nodes will accept different difficulties, at 2,016 block intervals each one calculates (and arrives at the same conclusion) the difficulty by checking the timestamp on the most recent solution it has received and compares this to the time stamp of the solution that came 2,016 solutions before the current one (2,016 in Bitcoin simply because there are 2,016 10-minute periods in a two week time frame and a block is mined approximately every 10 minutes).
This check can actually be performed sooner (instead of at 2,016 block intervals) this interval is simply the one used at Bitcoin. A smart contract could also provide regulation around the difficulty but that’s a different discussion.
The amount of time that has elapsed in Bitcoin should be 2 weeks, because solutions should be coming in at about 10 minute intervals. If the elapsed time is less, it means the difficulty is too easy and needs to be increased (automatically), if the elapsed time is more, if means the difficulty is too high and needs to be decreased. So that they can keep this constant 10-minute interval.
The reason they do this in Bitcoin is that they have a predetermined time by which they want all coins to be released, mining from then onwards will be exclusively paid by transaction fees and no longer by newly minted Bitcoins. Transaction fees are already part of the structure and you can see the fees paid for each block at blockchain.info or the block links above.
This gives Bitcoin “predictable scarcity”, I.e. no flooding the market with coins, one of the qualities that a unit of currency or barter must have to make it worth something (or at least a placeholder for something that is worth something).
If you look back at the block summary above, you will notice that the current time between the blocks is actually much more than 10 minutes, it sits closer to the 14 minute mark (which is 40% to high) and this indicates that there is likely a current decline in hash rate on the network (I.e. fewer miners) and may result in the next difficulty check generating a downwards adjustment of the difficulty to bring it closer to the 10 minute mark. This system is completely self-adjusting.
Other Information
As outlined above, there are a variety of “predetermined” hashes associated with public keys, private keys, block hashes, Merkle roots, etc.
To find out more about public and private keys are generated, and the use of different prefixes for hash addresses see the following links:
a. https://en.bitcoin.it/wiki/Address
b. https://en.bitcoin.it/wiki/List_of_address_prefixes
c. https://en.bitcoin.it/wiki/Technical_background_of_version_1_Bitcoin_addresses
Acknowledgements / References
As stated, the above is largely based on Azotic’s post on Reddit from February 2013 (https://www.reddit.com/user/azotic); he/she provided such a great explanation that I didn’t see the point in rewriting most of it. This chapter is purely here for reference in later chapters.
Artwork:
• Title page “Intelligent Solutions” courtesy of http://www.hloom.com/cover-pages/
• Page header “Abstract blue lights” created by Kotkoa - Freepik.com
Other references:
• https://blockchain.info/charts/hash-rate
• https://blockchain.info
• https://www.reddit.com/user/azotic
• https://blockchain.info/charts
Contact me
You can contact me here with any questions, suggestions and / or to discuss the topic of this document:
LinkedIn: https://www.linkedin.com/in/iwanspillebeen/
CryptoPub: https://thecrypto.pub/u/iwan.spillebeen
Disclaimer
Blockchain – Decrypted is written as a series of chapters, aimed at demystifying the various workings of blockchain technology. Where appropriate I use examples from existing or to-be cryptocurrencies, these examples are just that, examples, and do not aim at promoting or otherwise endorsing any given cryptocurrency.
This document does not constitute legal or financial advice and I do not make any guarantees or promises as to any results that may be obtained from using my content. No one should make any investment decisions without first consulting his or her own financial advisor and conducting his or her own research and due diligence. I disclaim any and all liability in the event any information, commentary, analysis, opinions, advice and/or recommendations prove to be inaccurate, incomplete or unreliable, or result in any investment or other losses.