Criptografía de Curva Elíptica de Bitcoin (ECDSA) explicada al detalle (Desentrañando los secretos de Bitcoin)

Ejemplo de curva elíptica ------ Fuente: Elaboración propia
En el presente artículo explicare la Criptografía de curva elíptica de Bitcoin (ECDSA) de la forma más sencilla que sea posible, pero sin descuidar el rigor matemático requerido, debemos recordar que los algoritmos de Criptografía Asimétrica tal como el ECDSA se basan en un par de claves, clave privada y clave publica, las cuáles básicamente son números, la clave privada corresponde a un número que nos permite gastar los fondos mientras que la clave pública es un número en base al cual se genera la dirección a la que se envía el dinero.
La clave pública puede ser generada a partir de la clave privada de forma fácil mientras que el proceso inverso es imposible de realizar con la potencia computacional existente en la actualidad. El proceso mediante el cual se genera la clave pública a partir de la clave privada se conoce como multiplicación de curva elíptica.
Para entender cómo funciona este proceso al detalle primero debemos entender algunos conceptos matemáticos importantes.
Cuerpos Finitos
Un cuerpo finito o campo finito, es un cuerpo definido sobre un conjunto finito de elementos, ¿Confundido? aclaremos que es un cuerpo.
Un cuerpo es una estructura algebraica formada por un conjunto y dos operaciones básicas llamadas adición y multiplicación (no necesariamente son iguales a la adición y multiplicación de números reales) que se pueden realizar entre todos los elementos del cuerpo y cumplen las propiedades: asociativa, conmutativa y distributiva de la multiplicación respecto de la adición, además de la existencia de elementos neutros e inversos tanto para la adición como para la multiplicación.
Es decir, si a, b y c pertenecen al cuerpo K y a es distinto de 0 entonces deben cumplirse las siguientes propiedades:
Se debe recordar que el elemento neutro para la adición se denota por 0 pero no necesariamente corresponde al número real cero, lo mismo aplica para el elemento neutro multiplicativo (1). Un ejemplo de cuerpo son los números racionales ya que los mismos cumplen con todas las propiedades listadas anteriormente, los números racionales son un cuerpo infinito como es evidente.
El cuerpo de los enteros modulo P
La aritmética modular consiste en un sistema aritmético para clases de equivalencias de números enteros, se basa en realizar la adición o multiplicación de dos números de forma similar a la adición y multiplicación en el conjunto de números enteros y luego calcular el residuo al dividir entre un número entero llamado modulo (denotado por p), por ejemplo:
5 + 10 = 2 (modulo 13) debido a que 5 + 10 = 15 luego 15/13 es 1, y el residuo es 2
12 + 10 = 9 (modulo 13)
12 * 10 = 3 (modulo 13) debido a que 12 * 10 = 120 luego 120/13 es 9, y el residuo es 3
6 * 6 = 1 (modulo 7)
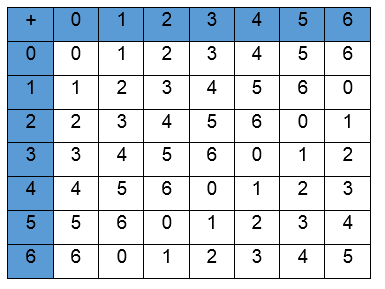
El conjunto de los enteros módulo p consiste en todos los números enteros desde 0 hasta p−1 con las operaciones de adición y multiplicación basadas en la aritmética modular (modulo p) también conocida como “aritmética del reloj”.
Un ejemplo sería el conjunto de enteros módulo 7, el cual está conformado por el conjunto numérico {0,1,2,3,4,5,6} y las dos operaciones adición y multiplicación en aritmética modular, las tablas de esas dos operaciones serían las siguientes:

Tabla N° 2 Multiplicación en F7
Se puede verificar cualquiera de las operaciones mostradas en las tablas, por ejemplo:
5 * 4 = 6 (modulo 7) debido a que 5 * 4 = 20 luego 20/7 es 2, y el residuo es 6
Para que el conjunto de los enteros módulo p sea un cuerpo, p debe ser un número primo, este requisito asegura que todos los elementos del conjunto tendrán un inverso multiplicativo. El conjunto de enteros módulo 4 no es un cuerpo debido a que 2 no tiene inverso multiplicativo, es decir, no existe solución para la ecuación:
2 * x = 1 (modulo 4)
Los cuerpos de enteros modulo p los denotaremos por Fp, en cuanto a los inversos aditivos debemos recordar que el inverso en F7 de 3 no es (-3) sino más bien 5, debido a que
3 * 5 = 1 (modulo 7)
Inversos multiplicativos modulo P
En cualquier cuerpo finito todo elemento distinto de 0 tiene un inverso multiplicativo según podemos ver en la tabla n° 2 para el cuerpo de los enteros módulo 7, se cumple:
1 * 1 = 1 (módulo 7)
2 * 4 = 1 (módulo 7)
3 * 5 = 1 (módulo 7)
4 * 2 = 1 (módulo 7)
5 * 3 = 1 (módulo 7)
6 * 6 = 1 (módulo 7)
En este caso pudimos encontrar los inversos multiplicativos usando las tablas previamente construidas, para cuerpos finitos con un valor de p muy grande se utiliza el algoritmo de Euclides extendido el cual permite encontrar el inverso multiplicativo de un elemento en un cuerpo finito. Lo importante es comprender que mientras p sea primo, siempre existirá un inverso multiplicativo para cada elemento.
Curvas elípticas en cuerpos de enteros módulo P
En general, una curva elíptica en Fp, es una función definida de la siguiente forma
O visto desde la perspectiva de adición y multiplicación dentro de Fp
En el caso de Bitcoin la curva elíptica usada se define específicamente en el estándar secp256k1 de la siguiente forma:
Donde p es igual a:
Por lo tanto el valor de p es un número bastante grande, esto quiere decir que el cuerpo Fp posee una gran cantidad de elementos (específicamente p elementos) así que encontrar las tablas de adición y multiplicación para este cuerpo no es computacionalmente posible, sin embargo se resuelven las operaciones para cada caso particular.
Dada la curva:
Los pares (x,y) que satisfacen dicha ecuación representan el conjunto de puntos de la curva elíptica, es importante señalar que esta curva posee un número total de puntos igual a:
115792089237316195423570985008687907852837564279074904382605163141518161494337
Para los ejemplos que se mostrarán en el presente artículo se usarán curvas elípticas con un valor de p más pequeño, en el caso de la curva secp256k1 el número de puntos totales es menor al valor de p.
Ejemplo de curva elíptica:
Esta curva elíptica viene dada por la misma función de la curva elíptica de Bitcoin pero se ha cambiado el valor de p, la gráfica de dicha curva se muestra a continuación.
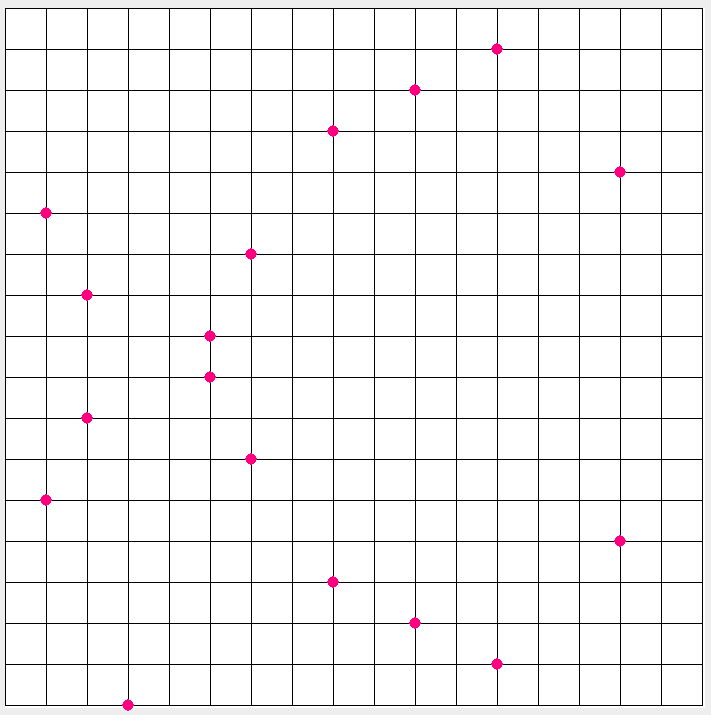
Curva elíptica en F17 ------ Fuente: Elaboración propia
Los puntos de esta curva son los siguientes
(1,5) ; (1,12) ; (2,7) ; (2,10) ; (3,0) ; (5,8) ; (5,9) ; (6,6) ; (6,11) ; (8,3) ; (8,14) ; (10,2); (10,15) ; (12,1) ; (12,16) ; (15,4) ; (15,13)
Según se muestra en la gráfica esta curva posee 17 puntos, esta gráfica se suele denominar curva elíptica debido a que es una proyección de la curva elíptica real:
Se puede observar que la curva elíptica en F17 es más bien una proyección de puntos dispersos en un plano bidimensional de números enteros menores que p. Para cualquiera de los puntos mostrados podemos verificar que se cumple la ecuación de la curva elíptica, por ejemplo para (10,15)
Casi todos los puntos tiene un punto simétrico dentro de la curva, por ejemplo (10,2) y (10,15) son puntos simétricos, en general los puntos simétricos son de la forma (x1, y1) y (x1, p-y1), la excepción seria el punto (3,0) debido a que aplicando la formula su inverso seria el mismo punto.
Grupo Abeliano a partir de una curva elíptica
Un grupo es una estructura algebraica formada por un conjunto y una operación básica llamada adición (no necesariamente igual a la adición de números reales) que se puede realizar entre todos los elementos del grupo, la adición en un grupo es asociativa y tiene un elemento neutro.
Es decir, si a, b y c pertenecen al grupo K
a + b pertenece a K (K es cerrado para la adición)
( a + b ) + c = a + ( b + c ) (Asociatividad de la adición)
a + 0 = a (Elemento neutro para la adición)
Un grupo abeliano es un grupo en el cual la operación interna es conmutativa es decir
a + b = b + a (Conmutatividad de la adición)
Dados los punto de la curva elíptica
Y un punto adicional llamado “punto al infinito” (0,0), el cual no satisface la ecuación de la curva se forma un grupo abeliano, la operación de adición de puntos se define de la siguiente manera:
Tres puntos en una curva elíptica están alineados si su suma da cero P1 + P2 + P3= (0,0), es decir, P1+P2 = -P3 donde -P3 corresponde al punto simétrico a P3, adicionalmente podemos decir que tres punto en Fp están alineados si existe una línea recta que los conecta, sin embargo, las líneas rectas en Fp no son iguales a las líneas rectas en los números reales.
Una línea recta en Fp es el conjunto de puntos (x,y) que satisfacen la ecuación
Que es la misma ecuación para los números reales pero aplicando aritmética modular, por ejemplo en F17 los puntos (2,7) y (5,8) están alineados en la recta:
Probando con los otros puntos de F17 se demuestra que el tercer punto alineado en dicha recta es (12,16) por lo tanto el resultado de la adición es el simétrico de (12,16), es decir, (12,1) en caso de que se sume un punto P1 con el mismo, como no puede trazarse una línea recta entre ambos puntos, la línea recta se extiende para ser la tangente sobre la curva en P1, esta tangente intersectará a la curva en un punto, el simétrico de dicho punto es el resultado de la adición.
Propiedades de la adición de puntos
P1+ 0 = 0 + P1 = P1
P1+ (-P1) = 0 un punto más su simétrico es igual al punto al infinito
Las ecuaciones para calcular la suma de dos puntos son las siguientes, dados P1 =(X1, Y1) y P2 =(X2,Y2) su suma es igual a P3 =(X3,Y3)
La demostración de porque estas formulas funcionan va más allá del ámbito de este artículo. Ahora definimos la multiplicación escalar
Donde n es un número entero menor que p, por ejemplo en F17 si definimos P1 = (1,5) y multiplicamos por un escalar n obtendríamos los siguientes puntos dependiendo del valor de n

Tabla N° 3 Multiplicación escalar en F17
Al multiplicar por diferentes valores escalares tomando (1,5) como punto generador hemos obtenido un subgrupo cíclico compuesto por 9 elementos que se repiten continuamente, si queremos generar un subgrupo con un gran número de puntos debemos prestar atención al valor del punto generador que seleccionamos. En el caso de la curva elíptica de bitcoin el punto generador es el siguiente
X=55066263022277343669578718895168534326250603453777594175500187360389116729240
Y=32670510020758816978083085130507043184471273380659243275938904335757337482424
El punto obtenido al multiplicar el punto generador G por la clave privada es la clave pública la cual se suele representar en dos formatos diferentes, comprimida y descomprimida.
La clave pública descomprimida inicia con “04” seguido de la coordenada X en hexadecimal y luego la coordenada Y en formato hexadecimal, mientras que la clave pública comprimida inicia con “02” o “03” (si la coordenada Y es par inicia con “02”, en caso contrario inicia con “03”) seguido de la coordenada X en hexadecimal.
En síntesis el proceso de generar la clave privada a partir de la clave pública consiste en tomar la clave privada como numero escalar y multiplicarla por el punto generador de la curva secp256k1, el punto obtenido será la clave pública Bitcoin. Finalmente para obtener la dirección bitcoin a partir de la clave pública se aplican dos algoritmos de hashing, específicamente SHA256 y RIPEMD160 los cuales serán abordados en un próximo artículo.


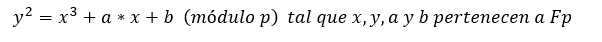

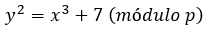



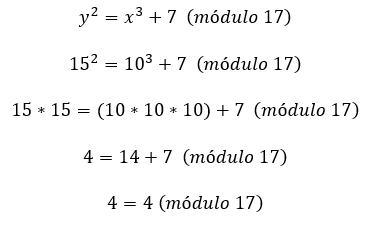
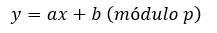

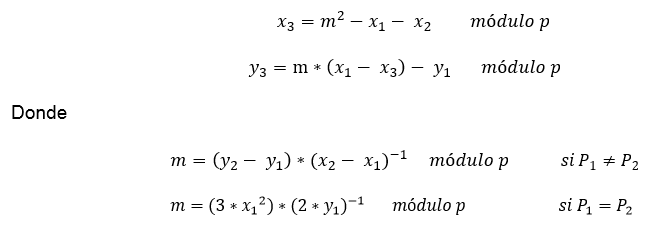

Te felicito!! Es un muy muy buen trabajo. He leído mucho acerca de como funciona bitcoin, pero nunca había bajado al detalle de conocer la fórmula para pasar de llave privada a pública.
Sería interesante abordar el tema de por qué no puede ser reversible. Entiendo que la clave aquí son los números grandes cuya factorizacion posee grandes números primos y por tanto es difícil de lograr.
Excelente post. Te dejo mi upvote y reestem.
Muchas gracias por tu apoyo, en relación a la reversibilidad del proceso de Multiplicación escalar en Curvas Elípticas, es decir, encontrar la clave privada a partir de la clave pública es un problema que se conoce como el Problema del Logaritmo Discreto en Curvas Elípticas (PLCDE) el cual es de extremada dificultad al punto que no puede ser resuelto con la potencia computacional y los algoritmos existentes en la actualidad, y aunque en el futuro se descubriera un algoritmo que resuelva este problema en tiempo polinomial debemos recordar que las direcciones bitcoin enmascaran la clave pública usando dos algoritmos de hashing el SHA256 y RIPEMD160, de allí la opinión de muchos usuarios de bitcoin entre los cuales me incluyo de no reutilizar direcciones una vez que hemos gastados los fondos, porque al firmar una transacción exponemos la clave pública la cual queda registrada en la blockchain.
Gracias por la respuesta. Esto de no reutilizar direcciones es en caso de que exista un algoritmo que resuelva en tiempo polinómico, pero como aun no existe no hay problema, cierto?
Claro por ahora no hay problema, pero se cree que con la llegada de la computación cuántica la seguridad de bitcoin podría verse afectada
saludos amigo tienes mi voto espero contar con el tuyo https://steemit.com/spanish/@davidjose28/problemas-con-bandwidth-remaining-o-limite-de-ancho-de-banda-excedido
Que buen trabajo! Si quiero citar tu articulo, cual es tu apellido e iniciales?