Latest Research Papers In Condensed Matter Physics | (Cond-Mat.Stat-Mech) 2019-01-27
Statistical Mechanics
IR-truncated 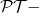 symmetric
symmetric 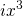 model and its asymptotic spectral scaling graph (1901.08526v1)
model and its asymptotic spectral scaling graph (1901.08526v1)
Uwe Guenther, Frank Stefani
2019-01-24
The
symmetric quantum mechanical
model over the real line,
, is infrared (IR) truncated and considered as Sturm-Liouville problem over a finite interval
. Via WKB and Stokes graph analysis, the location of the complex spectral branches of the
model and those of more general
models over
are obtained. The corresponding eigenvalues are mapped onto
invariant asymptotic spectral scaling graphs
. These scaling graphs are geometrically invariant and cutoff-independent so that the IR limit
can be formally taken. Moreover, an increasing
can be associated with an
constrained spectral UV
IR renormalization group flow on
. The existence of a scale-invariant
symmetry breaking region on each of these graphs allows to conclude that the unbounded eigenvalue sequence of the
Hamiltonian over
can be considered as tending toward a mapped version of such a
symmetry breaking region at spectral infinity. This provides a simple heuristic explanation for the specific eigenfunction properties described in the literature so far and clear complementary evidence that the
symmetric
models over the real line
are not equivalent to Hermitian models, but that they rather form a separate model class with purely real spectra. Our findings allow us to hypothesize a possible physical interpretation of the non-Rieszian mode behavior as a related mode condensation process.
Statistics of heat transport across capacitively coupled double quantum dot circuit (1901.08512v1)
Hari Kumar Yadalam, Upendra Harbola
2019-01-24
We study heat current and the full statistics of heat fluctuations in a capacitively-coupled double quantum dot system. This work is motivated by recent theoretical studies and experimental works on heat currents in quantum dot circuits. As expected intuitively, within the (static) mean-field approximation, the system at steady-state decouples into two single-dot equilibrium systems with renormalized dot energies, leading to zero average heat flux and fluctuations. This reveals that dynamic correlations induced between electrons on the dots is solely responsible for the heat transport between the two reservoirs. To study heat current fluctuations, we compute steady-state cumulant generating function for heat exchanged between reservoirs using two approaches : Lindblad quantum master equation approach, which is valid for arbitrary coulomb interaction strength but weak system-reservoir coupling strength, and the saddle point approximation for Schwinger-Keldysh coherent state path integral, which is valid for arbitrary system-reservoir coupling strength but weak coulomb interaction strength. Using thus obtained generating functions, we verify steady-state fluctuation theorem for stochastic heat flux and study the average heat current and its fluctuations. We find that the heat current and its fluctuations change non-monotonically with the coulomb interaction strength (
) and system-reservoir coupling strength (
) and are suppressed for large values of
and
.
A simple closure procedure for the study of velocity autocorrelation functions in fluids as a "bridge" between different theoretical approaches (1901.08501v1)
V. V. Ignatyuk, I. M. Mryglod, T. Bryk
2019-01-24
Velocity autocorrelation functions (VAF) of the fluids are studied on short- and long-time scales within a unified approach. This approach is based on an effective summation of the infinite continued fraction at a reasonable assumption about convergence of relaxation times of the high order memory functions, which have purely kinetic origin. The VAFs obtained within our method are compared with computer simulation data for the liquid Ne at different densities and the results, which follow from the Markovian approximation for the highest order kinetic kernels. It is shown that in all the thermodynamic points and at the chosen level of the hierarchy, our results agree much better with the MD data than those of the Markovian approximation. The density dependence of the transition time, needed for the fluid to attain the hydrodynamic stage of evolution, is evaluated. The common and distinctive features of our method are discussed in their relations to the generalized collective mode (GCM) theory, the mode coupling theory (MCT), and some other theoretical approaches.
Simultaneous Phase Separation and Pattern Formation in Chiral Active Mixtures (1901.08496v1)
Demian Levis, Benno Liebchen
2019-01-24
Chiral active particles, or self-propelled circle swimmers, from sperm cells to asymmetric Janus colloids, form a rich set of patterns, which are different from those seen in linear swimmers. Such patterns have mainly been explored for identical circle swimmers, while real-world circle swimmers, typically possess a frequency distribution. Here we show that even the simplest mixture of (velocity-aligning) circle swimmers with two different frequencies, hosts a complex world of superstructures: The most remarkable example comprises a microflock pattern, formed in one species, while the other species phase separates and forms a macrocluster, coexisting with a gas phase. Here, one species microphase-separates and selects a characteristic length scale, whereas the other one macrophase separates and selects a density. A second notable example, here occurring in an isotropic system, are patterns comprising two different characteristic length scales, which are controllable via frequency and swimming speed of the individual particles.
Evidence for Supersymmetry in the Random-Field Ising Model at D = 5 (1901.08473v1)
Nikolaos G. Fytas, Victor Martin-Mayor, Giorgio Parisi, Marco Picco, Nicolas Sourlas
2019-01-24
We provide a non-trivial test of supersymmetry in the random-field Ising model at five spatial dimensions, by means of extensive zero-temperature numerical simulations. Indeed, supersymmetry relates correlation functions in a D-dimensional disordered system with some other correlation functions in a D-2 clean system. We first show how to check these relationships in a finite-size scaling calculation, and then perform a high-accuracy test. While the supersymmetric predictions are satisfied even to our high-accuracy at D=5, they fail to describe our results at D=4.

Don't forget to Follow and Resteem. @condensed-matter
Keeping everyone inform.
Source
Copying/Pasting full or partial texts without adding anything original is frowned upon by the community. Repeated copy/paste posts could be considered spam. Spam is discouraged by the community, and may result in action from the cheetah bot.
More information and tips on sharing content.
If you believe this comment is in error, please contact us in #disputes on Discord
Hi! I am a robot. I just upvoted you! I found similar content that readers might be interested in:
https://arxiv.org/abs/1901.08512