The Surefire Way of Investing: How best to spend your money
Compound Interest - Math neves lies
Compound interest is the eighth wonder of the world. He who understands it, earns it ... he who doesn't ... pays it.
- Albert Einstein
"Cool dude. Sounds epic. Einstein knew his shit, I guess. But what actually is compound interest ?"
It is really quite simple. We just need a little bit of math to start understanding why this effect is so powerful. Compound interest is what happens to a given sum, for example a cash stack, when it over a set unit of time increases by a set percentage. This phenomena is mathematically expressed by the following formula:
Where z is cash starting amount, p the interest rate, x the amount of time that has passed and Z(x) is our new stack after x amount of time.
Let's put in some numbers.
Say you start off with 1000 USD. Then z will be substituted for this amount. The most likely place for the money to be situated is in the bank, maybe in savings account, which for the purpose of this example we'll guess offers a return rate of 0.5 %. Then p should have a value of 1.005. We now have our set values, and so the only variable which ultimately decides our final value Z is time; represented byx. And since rate of return promised by the bank is annual, will x be the number of years the cash has been chilling in the savings account.
So, after one year the amount of money will have accumulated by:
Not much all thing considered. The interesting thing however, is that now we have a new, higher value which will receive the same 0.05 %. I admit that it still does not sound all that impressing. Even after the a good few years the results fail to compel.
Two years:
"Hmmm. Seems more like we are just getting an annual flat amount of 5 dollars instead of any percentage."
Yup, 0.05 % is really low, practically speaking. It is not until four years have gone by before you can start counting anything more than the +5 USD / year, and then only cents!
It is clear that we need to up the amount of time. A decade lends a somewhat better view of where this savings account is going.
We see that this number is still just a tiny bit bigger than what our exceptions from that first impression of +5 USD / years initially would tell us. In fact, we are doing a mighty 1 dollar better!
Disappointed or not, at least now we we have a mathematical understanding behind the concept. We continue with the use of a graph, whereby the formula's sleeping potential may really come to light.
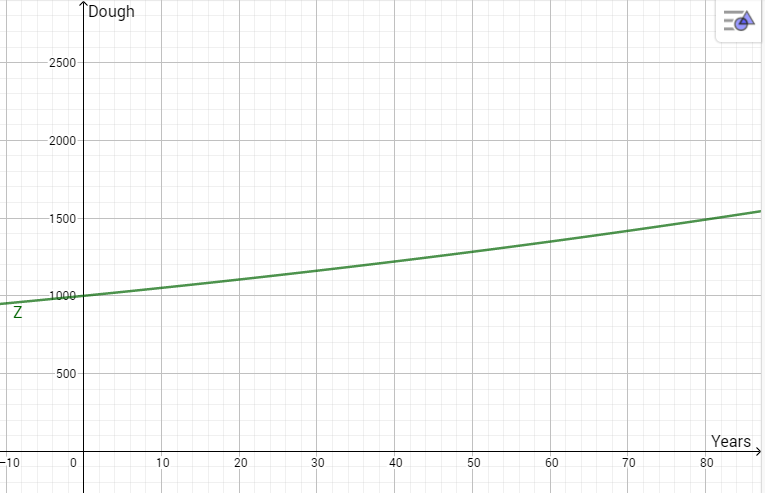
"Wow."
"That's really..."
"...really..."
"...REALLY..."
"...SHITTY."
Damn right! To you, the banking option presents only one real benefit, namely the safekeeping of your money. The interest rate should only be seen as a small bonus helping to protect value of your capital against inflation. Although, it should be said, chances are that the offered rate in fact is lower than the that of the inflation, meaning that your money is slowly decreasing in actual purchasing power!
Ok. So at the very least we now see that the idea of the savings account is an empty sack of straw. There is nothing to it in terms of effective accumulation. Admittedly, the interest rate used in this example probably toward the lower end of what most banks could provide, but for you to get the best deal (and then we're not even talking 2 %) you would commit to making your liquid capital quite immobile for a fairly long time.
Higher interest rates are usually only granted when you do some or all of the following:
Better rate always translates into the worsening of the other conditions.
But what if we just hold for a really long time, so that x gets huge
Sure. Let's have a look at the same graph, now with much higher values of x.

Holy boly! After 1200 the stack will have grown to roughly 400 000 USD! That translates into far more than just +5 USD / Year. In fact, from that year to the next the holding would increase by 2000 USD.
"Fuck yeah, dude! Let's build a time machine, travel back to 30 AD, steal Judas' 30 pieces of silver, put them in a savings account and then back to the future for SAVAGE CASH!"
YEAAAAH. We would make:
Except for the fact that we forgot to adjust for inflation. 2% yearly loss in respect to purchasing power is expected:
Ops! We would be losing money from the get-go.
Ok. So I guess banks suck?
Well, math doesn't lie. Banks are certainly a below par option when it comes to looking after the longevity of your wealth. We we want to receive the benefits of compounding interests, we need to make sure that ? can beat out the inflation. But which investment is the surefire way to achieve just that?
Long-term Growth
Of course, if our investment is to yield any profits, it need to be allocated to something which can provide some sort of value: meeting a need with a solution we find helpful. We humans have always created value in this sense, and we will continue to do so until the end of times. This ceaseless creation of value is a cornerstone of our worldview: we always strive toward making things better. It is the foundations of economics and therefore what allows us to have confidence in our investment.
Then why do so many of us actually lose money in the markets? Aren't you painting the an overly optimistic picture of things?
Yes, short term most of us leave the markets poorer than we arrived. Especially day-traders, 90 % of which go in the red. One way of explaining this loss of value (how I currently see it anyway) is as a result which can play itself out in the short-term by virtue of our own flaws. The awareness that we are creating value will occasionally corrupt us; greed and blind optimism lead to bad assessments as to the real worth of something. But long-term we are still creating value, so if our investment operates on a sufficiently long timescale, we should be set.
Gold?
Nope. That's a bet against growth.
Property?
Ok, if you can afford it. Naaaa, we'll start looking at stocks and how we can make an investment in the stock market grant compounding growth.
Let's say you have 500 bucks you want to invest in the stock market. How do you go about it? Do you put it all into one promising player or do you spread it out? Given how we are only interested in long-term performers, you would have to invest in something you would be comfortable holding even if you went to jail for five years. If you can justify that level of confidence, it probably an excellent pick. Though not risk free. And since we want a method which approximates guaranteed returns, this approach fails. Even if you were willing to bet your life on your one winner investment, you still can't predict the future. It could all go to shit. Shit we need to protect ourselves against.
Index Fund
Having faith in one particular stock could more often than not be translated into having confidence in the market that stock represents. If we spread our investment across all stocks, we massively decrease our risk. Through diversification we protect ourselves from being burned as a result of one company's failure.
BORIIING! No risk, no reward, right?
Not at all. This attitude toward investing is arguably the most successful one. Index Funds are passively traded mutual funds which simply mimic the market as a whole. That is to say that if the market index goes up 2%, so does your investment. This is in contrast to actively traded funds, which are trying to beat the market.
But then surely it's better to invest in an actively traded fund?
Yeah, one would think so, right? Though the fact is that 96% of all mutual funds don't beat the index. Plus the fees are higher. Now let's have a look at the S&P 500 Index Fund.
The S&P 500 is an index fund consisting of roughly 500 american large-cap companies.
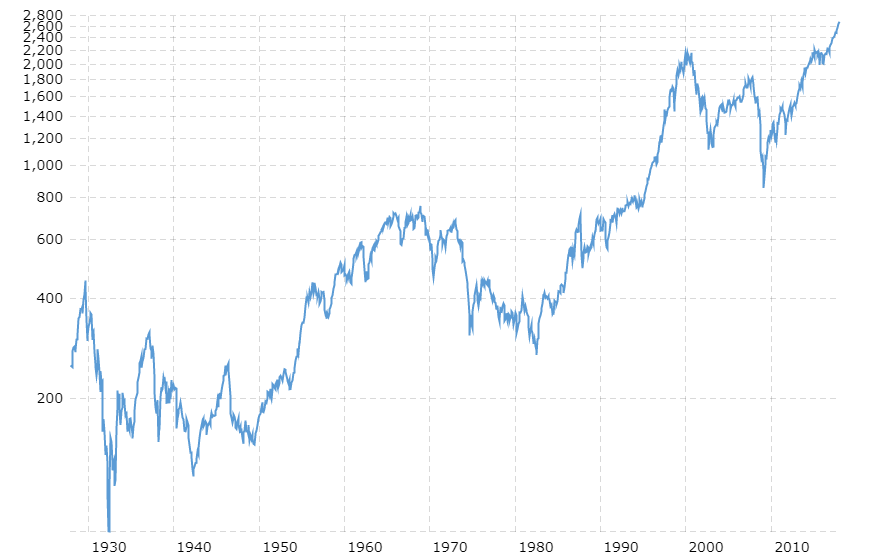
Not bad. With an average annual return of 7 % (adjusting for inflation) it tells a whole 'nother tale when implemented into our familiar formula.

30 000 USD after 50 years, from an initial investment of only 1000 USD is not bad at all.
Well, sure that's quite alright. But the S&P graph shows some clear recessions. What if you accidentally bought a top?
Good point. Luckily it's a risk we don't a have to accept. Remember how we are only operating on a long-term scale? That is why we diversify. And that is why we won't spend all our ammunition at once, but rather a set sum periodically. Once a week or once a month for example. This is called dollar cost averaging and helps mitigate the risk you expose yourself to. When the market goes down you receive more shares, while when it goes up you receive fewer, but your previous buys appreciate in value. This approach is an effective hedging strategy against volatility and a thus a notably effective tool for investing in cryptocurrencies.
It's all about them Cryptos
Of course, the twist at the end is that this investing strategy is the perfect way to tackle the crypto market. In some sense, applying it to cryptos is even easier: Bitcoin is already functioning as the index, having every other currency pegged to it. Bubble or not, if you have long term faith in this market, just slowly buy your way into Bitcoin. Then you get the best of both worlds.
Nice to see you back again @fisch. With the strong SBD things are looking good. Yes, compound interest is the strongest force in the Universe, but most people do not get it. You just reminded me that I have bought to much silver lately. Precious metals just keep up with CPI over time. Stocks is the King. One of my favourites books on stocks focusing on compound interest and stuff is Stocks for the Long Run by Jeremy Siegel.