Modeling one's return as a function of Worst Case Risk-Adjusted Return
Below I will show some modeling for a general portfolio optimization problem. In this portfolio, we are trying to find an optimal Worst-case Risk Adjusted Return given a vector of expected returns. We do not know exact details about the covariance matrix of our returns, however. We do have upper and lower bounds on each value of our covariance matrix as well as a positive semi-definite covariance matrix. Under the assumption that we are not expert investors and have varying non-negative risk-tolerance levels, we will only take long positions in our portfolio and only make investments in stocks that have positive mean valued returns. One can formulate the problem as follows:
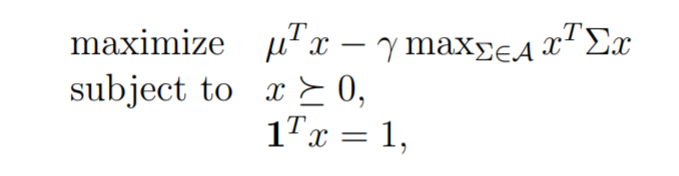

In this form, A serves as the region of all possible covariance matrices, x serves as the weight vector we are trying to find for our portfolio, Sigma is our covariance matrix, and gamma serves as our specified risk metric.
Note: the lower that gamma is, the lower we weight it in our multi-objective function and therefore it has an inverse relationship with risk-tolerance.
One can reformulate this as a semidefinite programming problem (a fancy way to say convex optimization problem) using the follow reformulation with the help of a principle called the Schur complement:
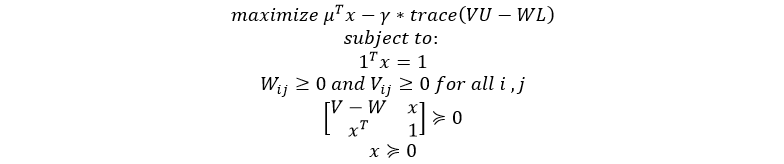
With a given dataset, I was able to compute the expected returns and worst-case risk as a function of the risk-tolerance parameter by solving the convex optimization problem stated above using a convex optimization toolbox.

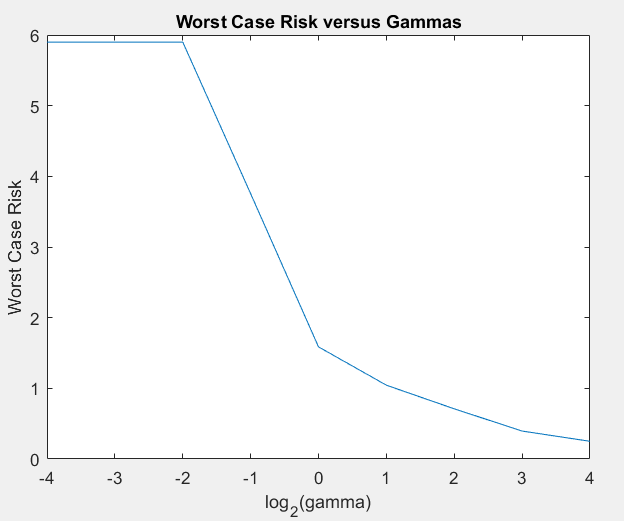
As gamma increases, we see that the overall returns decrease but so too does the risk profile of our portfolio. In fact, at a very small value of gamma at 0.0625 we see that the mean return is 11.2% with a worst-case risk variance of about 5.9%. We might consider that to be a little volatile (even though that would still yield a pretty decent return in a bad scenario). However, with a higher value of gamma at 1 we obtain a mean return of 8.847% with a worst-case-risk of 1.5865%. This does not have nearly as much upside as the previous gamma level but the return is more consistent and in a bad scenario would be more likely to yield a better return (in fact, it would be most likely to yield the best return in a bad market year). At the extreme case of gamma at 16, we have a poor expected return of 3.6780% with a worst-case risk of 0.2507% which means that are portfolio is nearly risk-free at the price of minimal returns.
I hope you enjoyed this exercise in Portfolio Optimization. If you have any questions, feel free to ask me below!
This post has received a 16.48 % upvote from @boomerang.
Good post Continue to work!
ohh yes stemians! do not forget ya Follow @gadisindo
gallery Female Indonesia and make us proud of her beautiful woman Indonesia! and vote too yes THANK YOU