"SLC-S22W1/Variables and Expressions"

Hari ini aku mengikuti kontes yang diadakan oleh @khursheedanwar tentang SLC S22W1//Variables and Expressions. Aku mengajak teman-teman untuk berpartisipasi pada kontes ini @teukuipul87 @zulbahri @assidiq.
A variable is a symbol or letter used to represent an unknown or changeable value in a mathematical expression.
Example: In a simple algebraic expression like “2x,” the letter “x” is a variable. This indicates that the value of “x” can vary depending on the situation or mathematical problem being discussed.
Exponential Expressions: Expressions that involve powers or exponents. Example: 2^x or e^(3x).
Logarithmic Expression: An expression involving the logarithmic function. Example: log(x) or ln(2x).
Practical Example
Suppose we want to know the relationship between temperature (x) and paint drying time (y). Experiments show that the relationship can be modeled by an algebraic expression:
y = 2x - 5
In this example:
- x is the independent variable (temperature)
- y is the dependent variable (paint drying time)
- 2x - 5 is the algebraic expression that describes the relationship between x and y.
(The more you will be detailed and accurate,the more your task will be perfect!)
No, evaluate is not the same as solve. Evaluate is used for expressions that do NOT have an equal sign. When evaluating, the value of the variable is given. Solve is used for equations that DO have an equal sign. When solving an equation, the value of the variable is not given.
To write and evaluate an expression, start by substituting the given values for each variable into the expression. Then use the order of operations, also known as PEMDAS, to simplify the expression.
The first step in evaluating an expression is to identify the values assigned to each variable, and then substitute those values into the expression for those variables.
Evaluating an expression with exponents means taking the base of the exponent and multiplying it by itself as many times as the exponent itself represents. For example, if we have three squared, that means multiplying the base 3 by itself twice. The final answer is three times three, which equals 9.
Simplify this expression: 3(2x - 1) + 2(x + 4) - 5


Evaluate this expression: (x^2 + 2x - 3) / (x + 1) when x = 2
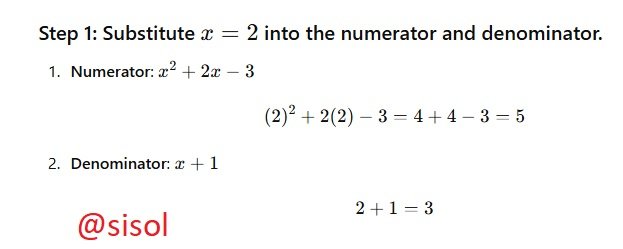

Solve the following equation: 2x + 5 = 3(x - 2) + 1


Suppose there's a bakery selling a total of 250 loaves of bread per day. They are selling whole wheat and white bread loaves with numbers of whole wheat loaves sold being 30 more than the number of white bread loaves. If x is representing number of white bread loaves sold out and bakery is making a profit of $0.50 for each white bread loaf and $0.75 for each whole wheat loaf then please write an expression for representing bakery total daily profit.
- Total loaves sold per day: 250.
- Whole wheat loaves sold 30 more than white loaves.
- x: number of white loaves sold.
- Profit per white loaf: $0.50.
- Profit per whole wheat loaf: $0.75.




Suppose that cost of renting a car for a day is re-presented by the expression 2x + 15 and here x is the number of hours in which car is rented. If the rental company offers a package of 3x - 2 dollars for customers who take car at rent for more than 4 hours then write an expression for the total cost of renting the car for x hours and show how you simplify it.

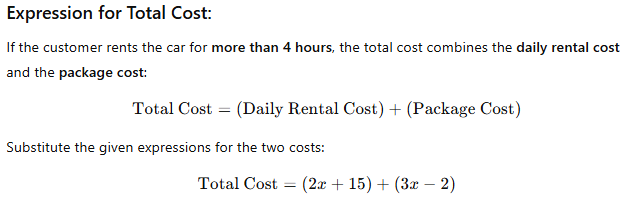

Regards @sisol