알고리즘 공부 Part2 : 최대공약수 찾기
이번 포스팅에서는 최대 공약수를 찾는 알고리즘에 대해서 공부 해보겠습니다.
예제는 전부 Python으로 작성하였습니다.
최대 공약수
최대 공약수란 주어진 두 정수의 약수 중에서 가장 큰 공통이 되는 약수를 말합니다.
예를들어 100과 30의 최대 공약수를 구해 봅시다.
100 약수 : 1,2,4,5,10,20,25,50,100
30 약수 : 1,2,3,5,6,10,15,30
이중 공통이 되는 약수는 1,2,5,10 이고 가장큰 최대 공약수는 10입니다.
보통 소인수 분해를 통해 구하게 되는데
| 2 | 100 | 30 |
|---|---|---|
| 5 | 50 | 15 |
| 10 | 3 |
아래 표와 같이 2와 5로 나눈후 더 이상 떨어지는수가 없어 2 * 5 = 10을
최대공약수로 구합니다.
유클리드 알고리즘
위의 30과 100은 10이라는 최대 공약수를 가집니다. 이 최대 공약수를 G(Greatest Common Divisor) 라고 가정합시다.
A = aG (30 = 3 * 10)
B = bG (100 = 10 * 10)
여기서 a와 b는 G(최대 공약수)를 제외한 값들을 곱한 값을 의미 합니다. 그리고 a와 b는 서로소(공통되는 약수가 1밖에 없는 경우)입니다. 예를들어 3의 경우 약수는 1,3이고 10은 1,2,5,10 입니다. 따라서 공약수는 1입니다.
a-b와 b는 서로소이기 때문에 A-B와 B의 최대 공약수 역시 G입니다. 공식은 아래와 같습니다.
A-B = a * G - b * G = (a-b) *G
함수의 이름은 Greatest Common Divisor의 약자로 GCD로 정하겠습니다.
def GDG(a,b):
if a < b :
t = a
a = b
b = t
a = a - b
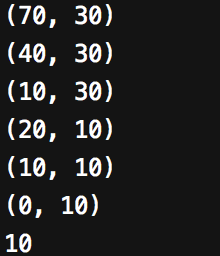
print (a, b)
if (a == 0) :
print(b)
return b
GDG(a,b)
if __name__ == '__main__':
GDG(30, 100)
유클리드 알고리즘 개선
a와 b값이 차이가 크게 되면 실행시간이 오래 걸립니다. 위의 예제의 경우 6번 실행하면 결과가 나옵니다. 하지만 1과 2000의 최대 공약수를 구할경우 2000번 실행해야 합니다. 따라서 이 문제를 해결해야 합니다.
30과 100의 공약수를 구하는 과정을 보면 (10,30)이 구간 입니다. 이 값을 보면 10은 100/30의 나머지와 동일 합니다.
100 - (30*3) = 10
따라서 %연산을 이용하여 나머지를 구하고 시작한다면 실행횟수를 줄일 수 있습니다.
개선한 코드는 아래와 같습니다.
def GDG(a,b):
t = a % b
a = b
b = t
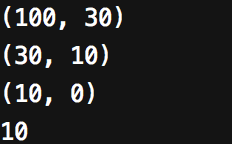
print (a, b)
if (b == 0) :
print(a)
return a
GDG(a,b)
if __name__ == '__main__':
GDG(30, 100)
다음과 같이 개선하면 실행 횟수가 3번으로 줄어든것을 보실수 있습니다.
오늘 포스팅은 여기까지 입니다.
감사합니다.
[소통의 가치 이벤트 #마지막회]에 참여해주셔서 감사합니다. 더 좋은 이벤트로 돌아오겠습니다!^^
즐거운 스팀잇 함께 만들어요!
스팀잇 가즈아!!!!!!!!!!
일교차가 큰 날씨에요 감기조심하세요^^
오늘은 비가 온다고 합니다 우산챙기세요
네 오치님도 감기 조심하세요^^
짱짱맨 호출로 왔습니다.