[쉽게 풀어 쓴 상대성 이론] Chapter 2. 갈릴레이 변환과 갈릴레이 속도 덧셈 공식
안녕하세요. 훈하니 @hunhani입니다.
아인슈타인의 상대성 이론은 과학뿐만 아니라 철학에도 많은 영향을 미쳤습니다. 근대까지만 하더라도 서양에서는 과학과 철학은 하나의 학문이었죠. 철학이 세상의 모든 진리를 탐구하는 학문이기 때문에, 자연의 진리를 탐구하는 과학도 철학의 일부였던 것입니다. 아인슈타인은 "철학은 과학으로부터 결론을 얻어야 한다."고 이야기했습니다. 이처럼, 상대성 이론은 자연과학이나 공학을 전공하는 사람들은 물론 인문사회학을 하는 사람들에게도 절실히 필요한 것이 아닐까 합니다. 과학의 범주를 넘어 누구나 알아두면 도움이 되는 상대성 이론에 대해 [쉽게 풀어 쓴 상대성 이론] 시리즈에서 차근차근 알아가 보도록 하겠습니다. 이전에 포스팅 했었던 물리학도가 들려주는 인터스텔라를 더 재밌게 보기 위한 18가지 이야기과 암호화폐가 100% 망한다고 양자 컴퓨터와 블록체인 보안 이야기에서 상대성 이론에 대해 아주 가볍게 언급했었죠? 이번 시리즈를 통해 보다 자세하게 그러나 더 쉽게 전달해드리도록 노력하겠습니다.

관성계와 갈릴레이 변환
모든 운동은 상대적이며, 등속 운동을 하는 모든 관찰자에게는 동일한 물리 법칙이 적용된다는 갈릴레이의 상대성 원리를 이해하셨다면 이번에 다룰 내용은 훨씬 더 쉽게 느껴지실 것입니다.
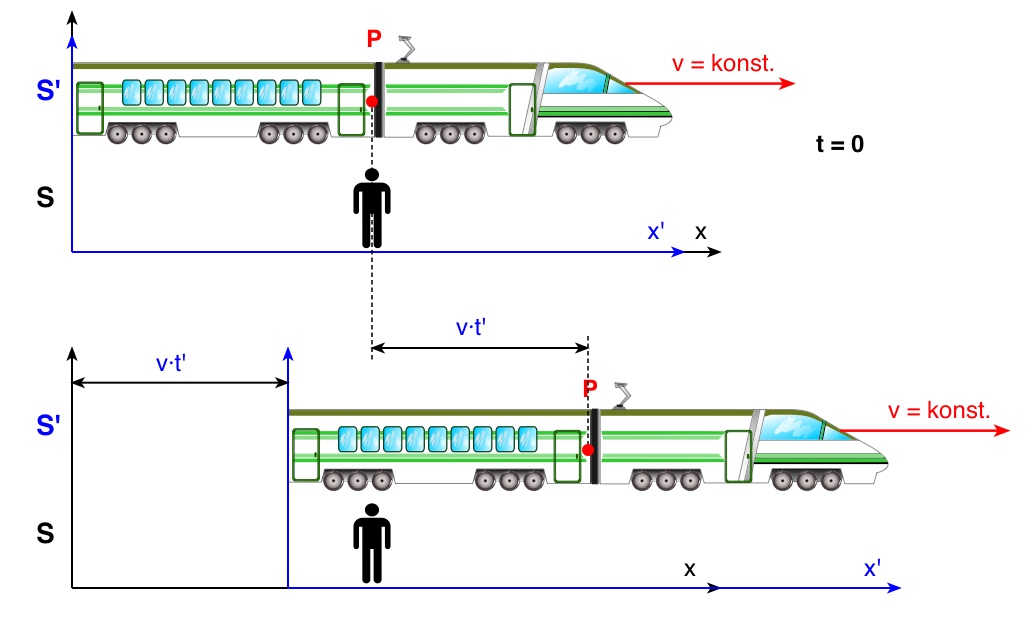
등속 운동하고 있는 기차와 가만히 서있는 관찰자를 생각해보겠습니다. 초기 시점, 관찰자는 기차의 P 지점을 바라보고 있습니다. 시간이 지나 정지 상태의 관찰자와 P 지점 사이의 거리는 어떻게 될까요? 등속 운동하는 기차가 해당 시간동안 이동한 거리에 해당하겠지요. 당연한 이야기지만 여기에 바로 갈릴레이의 상대성 원리가 숨어있습니다. 외부에서 힘이 작용하지 않으면 운동하는 물체는 계속 그 상태로 운동하려고 하고, 정지한 물체는 계속 정지해 있으려고 한다는 뉴턴의 1법칙, 즉 관성의 법칙을 들어보셨죠? 외부에서 다른 힘이 작용하지 않아 서로 정지하거나 등속 운동하고 있는 물체들의 모임을 관성계라고 합니다. 위 상황에서는 기차와 관찰자가 관성계에 해당하겠지요. 이러한 관성계에는 갈릴레이의 상대성 원리가 늘 적용됩니다.

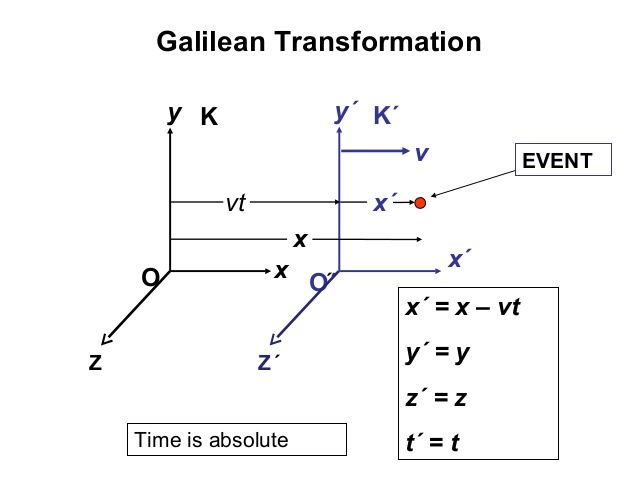
관성계에 속하는 두 직각좌표계가 정지 혹은 등속 운동을 할 때 한쪽 좌표계에서 다른 쪽으로 이동하는 변환을 갈릴레이 변환이라고 합니다. S(x, y, z) 및 S’(x’, y’, z’) 양 좌표계의 축이 서로 평행하고 좌표계 S’가 좌표계 S에 대해 x축의 +방향으로 일정한 속력 v로 운동할 때 시각 t의 변환식은 x’=x-vt, y’=y, z’=z로 주어집니다. 이러한 변환의 경우 **공간의 두 점 사이의 거리는 불변이고 뉴턴의 운동방정식도 그 형식을 변화시키지 않기 때문에 갈릴레이의 상대성 원리의 요구를 만족시키는 것이죠.

그동안 한 쪽은 정지해있고 다른 한 쪽은 등속으로 움직이는 상황만 다루었습니다. 이번에는 양 쪽 모두 등속으로 움직이는 상황을 생각해보지요. 자전거 탑승자는 초속 5m 속도로, 트럭 운전자는 초속 12m 속도로 같은 방향을 향해 움직이고 있습니다. 10초가 지나면 자전거 탑승자는 50m를, 트럭 운전자는 120m를 이동했겠지요. 자전거 탑승자 입장에서 트럭 운전자를 바라보면 10초 동안 몇 m 움직인 것으로 보일까요? 그렇습니다. 120m에서 50m를 뺀 70m이겠지요. 트럭 운전자가 움직인 거리에서 자전거 탑승자 자신이 움직이는 거리를 빼야합니다. 이동한 거리 대신 속도를 대입해도 마찬가지입니다. 트럭 운전자의 속도에서 자전가 탑승자의 속도를 빼야 자전거 탑승자 입장에서 바라본 트럭 운전자의 속도가 나오겠지요. 만약 같은 방향이 아닌 서로 다른 반대 방향을 향해 움직인다면 서로의 속도를 빼는 것이 아닌 더해야하는 것도 아시겠지요? 이처럼 각자의 운동 상태를 고려하여 서로의 속도를 더하거나 빼 한 쪽의 입장에서 다른 쪽의 운동 속도를 구하는 방법을 갈릴레이의 속도 뎃셈 공식이라고 합니다.
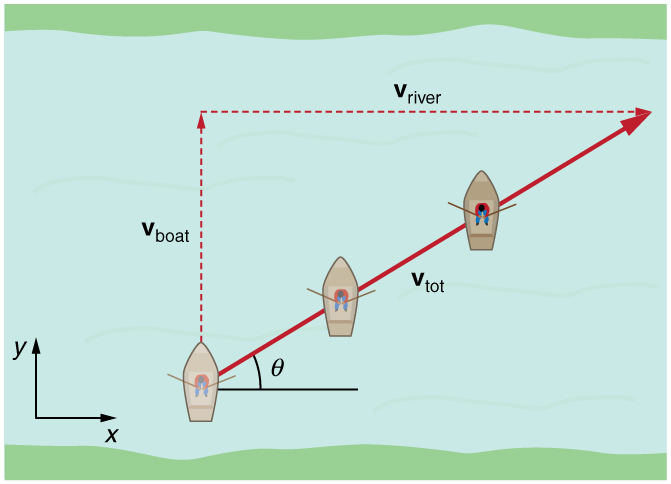
갈릴레이 속도 덧셈 공식을 이용하면 두 물체의 상대 속도를 계산할 수 있습니다. 상대 속도란 관찰자가 관찰하는 대상의 속도를 말합니다. 물체 A, B가 각자 운동하고 있을 때 물체 A와 같은 운동 상태에 있는 관측자가 B의 운동을 보았을 때의 속도를 A에 대한 B의 상대 속도라고 합니다. 관찰자와 관찰하는 대상이 각각 어떤 관성계에 있는지에 따라 상대 속도가 달라지지요. 같은 물체라도 관찰자에 따라서 서로 다른 좌표계를 도입하므로 대상의 속도는 그 크기와 방향이 달라집니다. 예를 들어, 배가 실제로 움직이는 속도를 구하려면 배 자체가 나아가는 속도에 흐르는 강물의 유속을 합해야 합니다. 비행기가 실제로 움직이는 속도를 구하기 위해 비행기가 나아가는 속도에 풍속을 더하는 것도 마찬가지 이유이죠.

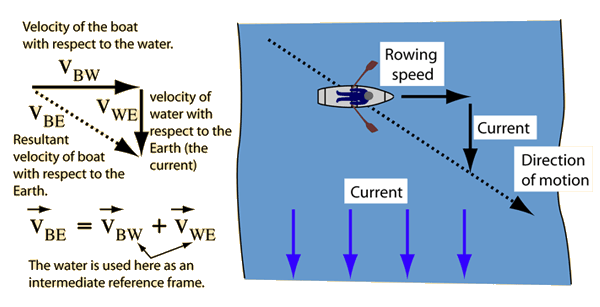
갈릴레이 속도 덧셈 공식은 너무나 간단하고 직관적이기 때문에 아무도 이 공식이 틀렸을 거라고 절대 생각하지 않았습니다. 갈릴레이 속도 덧셈 공식은 당대에 진리라고 믿는 물리 법칙이었죠. 하지만 결과적으로 갈릴레이의 상대성 원리, 갈릴레이 변환, 갈릴레이 속도 덧셈 공식 모두 운동 속도가 빛의 속도에 가까워질 경우 성립하지 않기 때문에 절대적인 진리가 아닙니다. 운동 속도가 빛의 속도에 가까워지는 상황은 아인슈타인의 상대성 원리를 적용해야 합니다. 정지 혹은 등속 운동을 할 때 한쪽 좌표계에서 다른 쪽으로 이동할 때 갈릴레이의 상대성 원리에서는 갈릴레이 변환을 사용하지만 아인슈타인의 상대성 원리에서는 로렌츠 변환을 사용하지요. 보다 정확히 말하자면, 운동 속도와 상관없이 일반적으로 사용할 수 있는 것이 아인슈타인의 상대성 원리이고 운동 속도가 빛의 속도보다 현저하게 낮으면 근사적으로 갈릴레이의 상대성 원리를 적용할 수 있는 것입니다.
다음 편을 기대해주세요!
지난 이야기
- [돈을 지배하는 물리 법칙] Chapter 0. 서론
- [돈을 지배하는 물리 법칙] Chapter 1. 시세에 작용하는 관성과 작용/반작용의 법칙
- [돈을 지배하는 물리 법칙] Chapter 2. 브라운 운동으로 해석하는 투기 이론
- [돈을 지배하는 물리 법칙] Chapter 3. 천체물리학자가 파헤친 주가와 주가 수익률의 관계
- [돈을 지배하는 물리 법칙] Chapter 4. 멱 법칙과 레비 안정 분포로 알아보는 빈익빈 부익부
- [돈을 지배하는 물리 법칙] Chapter 5. 켈리의 공식으로 알아보는 포트폴리오를 분산하는 방법
- [돈을 지배하는 물리 법칙] Chapter 6. 블랙-숄즈 주가 모형으로 알아보는 주가 변화와 자산의 위험 정도
- [암호화폐가 100% 망한다고? 양자 컴퓨터와 블록체인 보안 이야기] Chapter 0. 서론
- [암호화폐가 100% 망한다고? 양자 컴퓨터와 블록체인 보안 이야기] Chapter 1. 양자 컴퓨터! 도대체 일반 컴퓨터랑 뭐가 다른 거야?
- [암호화폐가 100% 망한다고? 양자 컴퓨터와 블록체인 보안 이야기] Chapter 2. 놀라운 자연의 마법, 양자 중첩/얽힘/순간이동
- [암호화폐가 100% 망한다고? 양자 컴퓨터와 블록체인 보안 이야기] Chapter 3. 병 주고 약 주는 양자 컴퓨터? 양자 병렬성과 양자 통신 보안
- [암호화폐가 100% 망한다고? 양자 컴퓨터와 블록체인 보안 이야기] Chapter 4. 큐비트를 이용한 양자 정보 처리
- [암호화폐가 100% 망한다고? 양자 컴퓨터와 블록체인 보안 이야기] Chapter 5. 양자 정보 세상을 위해 극복해야 할 기술적 난관
- [암호화폐가 100% 망한다고? 양자 컴퓨터와 블록체인 보안 이야기] Chapter 6. 양자 컴퓨터 기술 개발! 그래서 어디까지 진행되었나?
- [암호화폐가 100% 망한다고? 양자 컴퓨터와 블록체인 보안 이야기] Chapter 7. 양자 컴퓨터가 블록체인을 죽일 것이다?
- [밤하늘의 물리학] Chapter 0. 서론
- [밤하늘의 물리학] Chapter 1. 우주론의 기원과 진화
- [밤하늘의 물리학] Chapter 2. 정적인 우주와 동적인 우주
- [밤하늘의 물리학] Chapter 3. 연주 시차와 별의 밝기-거리 관계
- [밤하늘의 물리학] Chapter 4. 세페이드 변광성과 외부 은하
- [밤하늘의 물리학] Chapter 5. 허블의 법칙과 우주의 나이, 크기, 팽창률
- [밤하늘의 물리학] Chapter 6. 빅뱅 우주론으로 알아보는 우주의 탄생과 미래
- [밤하늘의 물리학] Chapter 7. 성간 물질과 별의 탄생 과정
- [밤하늘의 물리학] Chapter 8. 허블의 분류를 통해 알아보는 은하의 종류와 형태
- [밤하늘의 물리학] Chapter 9. 은하의 충돌과 분포 및 우주의 거대 구조
- [밤하늘의 물리학] Chapter 10. 성간운의 형태와 별빛의 편광
- [밤하늘의 물리학] Chapter 11. 성간운에서의 화학 반응과 외계 생명체의 단서
- [밤하늘의 물리학] Chapter 12. 별의 진화와 수명
- [밤하늘의 물리학] Chapter 13. 별의 최후와 갈색 왜성, 행성상성운, 백색 왜성, 초신성, 중성자별, 블랙홀의 탄생
- [수리물리학 이야기] Chapter 0. 서론
- [수리물리학 이야기] Chapter 1. 오일러 공식과 테일러 급수
- [수리물리학 이야기] Chapter 2. 크로네커 델타와 푸리에 급수
- [수리물리학 이야기] Chapter 3. 푸리에 해석과 푸리에 계수
- [수리물리학 이야기] Chapter 4. 푸리에 변환 및 역변환
- [수리물리학 이야기] Chapter 5. 팩토리얼과 감마 함수
- [수리물리학 이야기] Chapter 6. 가우스 함수와 가우스 적분
- [수리물리학 이야기] Chapter 7. 원통좌표계, 구면좌표계
- [수리물리학 이야기] Chapter 8. 물리학에서 자주 접하는 미분 방정식
- [수리물리학 이야기] Chapter 9. 좌표계 별 헬름홀츠 방정식의 일반해
- [쉽게 풀어 쓴 상대성 이론] Chapter 0. 서론
- [쉽게 풀어 쓴 상대성 이론] Chapter 1. 갈릴레이의 상대성 원리
- [알기 쉬운 물리학] 다양한 물리학 분야와 응집물질물리학 이야기
- [신의 입자] 만물에 질량을 부여하는 입자, 힉스에 대해 알아보자. (상편)
- [신의 입자] 만물에 질량을 부여하는 입자, 힉스에 대해 알아보자. (하편)
- [모든 힘은 어디에서 비롯될까?] 자연계에 존재하는 기본 4가지 힘에 대해 알아보자.
- [도플러 효과] 너와 나의 움직임이 진동수와 파장을 바꾼다?
- [차세대 초고속 이동수단] 하이퍼루프가 왜 특별한지 알아보자!
- [차세대 초고속 이동수단] 하이퍼루프가 지닌 문제점과 그 극복 방안
- [이공계 대학원생 근로계약 체결 관련] 4개 과학기술원 간담회에 다녀왔습니다.
- [수달, 두더지, 고라니, 멧돼지] 멸종위기 천연기념물이 사는 친환경 캠퍼스
- [3D 프린터 대축제] 3D 프린팅 갈라 in 울산
- [미국 물리학회 참석기] (8) 그래핀 연구의 세계적인 권위자 김필립 교수님을 만나다.
- [안철수 대표를 만나다] UNIST 잔디밭 토크 콘서트
- 물리학도가 들려주는 인터스텔라를 더 재밌게 보기 위한 18가지 이야기
- 그래핀 끼워 넣어 꿈의 다이오드 만들기
- 본문에서 사용된 모든 이미지는 구글 이미지에서 가져왔음을 밝힙니다.
- 본문을 작성하는데 있어 위키피디아 내용을 참조하였습니다.

Cheer Up!
this is a very good post buddy, but sorry my friend do not know what you say, because I do not understand japanese. but I know this is very interesting according to the pictures I see ..
Thanks. However, It is Korean, not Japanese.
yes friends ... if any time visit my blog buddy .. I am your followers mu friend. I always upvote and resteem your post.
점점 심도를 더해가는군요. 다음화 기대합니다.
@yoon 님의 과학 글도 기대하고 있습니다 ㅎㅎ #kr-science 태그만 돌다 보니 찾아뵙는걸 소홀했네요 죄송합니다~
오 이건 재밌어 보이네요.. 일단 댓글달고 내일 화장실서 정독하겠습니다.ㅋㅋ
화장실에서야말로 재미있는 것을 찾아보는 법인데 ㅎㅎ 영광입니다!
i don't understand anything but i like Einstein so much
and i hope you translate your blogs :)
followed
Sorry. I can not do it because of the time consuming to translate English. Anyway, thanks for your interest.
나중에 일반상대성이론도 다뤄주시나요?ㅎㅎ
물론이죠 ㅎㅎ 상대성 이론 전반을 모두 다루는 것이 목표입니다
학창시절 과학 시간이 생각나는 포스팅입니다^^ 앞으로의 연재도 기대할께요~
감사합니다 ㅎㅎ 앞으로도 꾸준히 연재하도록 하겠습니다
Interesting post - thanks @hunhani .
yes friends ... if any time visit my blog buddy .. I am your followers mu friend. I always upvote and resteem your post.
Thanks.
어제 글 읽고 스팀잇 먹통이여서 댓글을 못달았는데 이제 되네요 늘 느끼는 것이지만 참 깔끔하게 설명해주시는 듯해요^^
감사합니다 ㅎㅎ 설명히 깔끔하게 느껴지신다니 정말 뿌듯하네요 앞으로도 좋은 글 쓸 수 있도록 노력하겠습니다
우아...전문책 하나 내셔도 될거같으신데요?!!ㅎㅎ
높게 평가해주셔서 감사합니다 ㅎㅎ 시판되는 좋은 책이 많은데 전문책 수준까지 될런지요~ 스팀잇 포스팅으로 만족한답니다