Anatomy of a Proof - Why We Know For Sure Some Numbers Cannot Be Expressed as Fractions
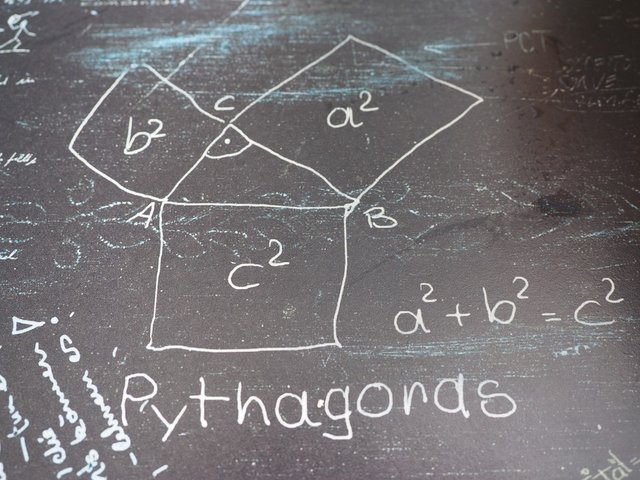
Pythagoras...
It all comes back to Pythagoras. You see, back in the very early days of worldly observations, all numbers were real. They were unit based quantities that represented all the items in the world one might observe.
So, whole numbers were very easy to comprehend as multiples of unit based items (0, 1, 2, 3, 4, etc.) So were integers, just by also including negative multiples of units (-3,-2,-1, 0, 1, 2, 3, etc.).
Rational Numbers might have been harder to process observationally, but still easy to understand. If you have a whole quantity and bisect it, you wind up with two equal parts. In other words, 1/2. Other fractions could be constructed similarly. The world was a great and orderly place, easily explained by mathematics.
So, imagine the horror of the Pythagoreans, when the following was discovered:
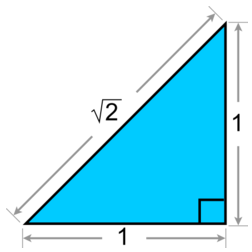
It is hard to say who first discovered this, but the concept was pretty simple. Take a square with side lengths each of one unit. Completely observable in the real world. Connect a line from diagonal to diagonal. Again, observable in the real world. Then, utilize the Pythagorean Theorem thusly:
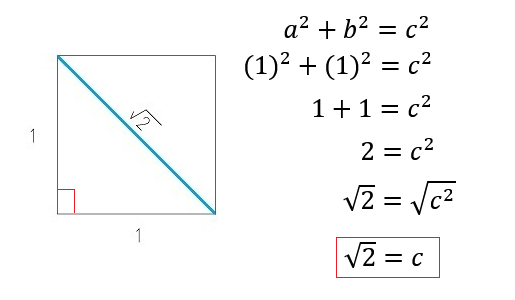
Now, at first, this probably wouldn't have bothered many in the era of the Pythagoreans. Historians believe they at first would have understood a square root with a rational approximation like so:
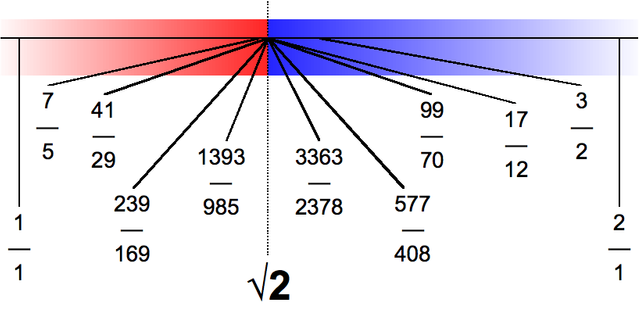
And why not? After all, if I am a Pythagorean, my whole world is explained by fractions. It would be incomprehensible to me to have a number represented any other way. That there could be "space between the spaces" would be shattering to your psyche. There was nothing irrational that could exist.
An irrational number was a sign of meaninglessness in what had seemed like an orderly world. The Pythagoreans wanted numbers to be something you could count on, and for all things to be counted as rational numbers. The discovery of an irrational number proved that there existed in the universe things that could not be comprehended through rational numbers, threatening not only Pythagorean mathematics, but their philosophy as well.
[Source]
Why are we so certain then that irrational numbers exist?

While we have no idea who first proved this, Hippasus of Metapontum is often one of the first that is credited. Not because of any eloquent proof that we know of or anything like that, but because of the legend of what happened when he did.
The discovery of irrational numbers is said to have been shocking to the Pythagoreans, and Hippasus is supposed to have drowned at sea, apparently as a punishment from the gods for divulging this.
[source]
Yet another lesson of many from history about how standing up for a true scientific belief can have terrible consequences.
Proof by Contradiction
While there no doubt that Innumerable mathematicians in history have dipped their toes in the proof of irrational numbers, one of the most famous setups involves a proof by contradiction.
Such a proof involves assuming the opposite of what you want to show is true and then somehow showing that assumption must be false.
For example of a proof by contradiction, how would we know there is no largest real number?
- Assume the contrary. There is a largest real number in existence. We are now going to try to contradict this in the steps that follow.
- Since this largest real number exists, we could add 1 to it, just like any other real number that exists.
- However, this number would now be logically larger than the number we assumed was the largest real number in existence.
- SINCE THIS COMPLETELY CONTRADICTS OUR FIRST ASSUMPTION, our first assumption must be false. There is no largest real number in existence.
Let's prove it then!
- Suppose
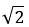 is rational. We are now going to try to contradict this in the steps that follow.
is rational. We are now going to try to contradict this in the steps that follow.
- This would mean we could express
as a ratio of two integers, p and q as follows:
- We can assume, at this step, that p and q have no common factors. If they did, they would have been already canceled. For instance, if p = 8 and q = 4:
- By squaring both sides of our formula, and simplifying a little, we would get the following:
- Now, here's where the fun comes in. We now know that
must be an even number. Why? Because it is equal to twice of another number. Remember...any even number in this world is always a multiple of two.
- Since
is even, we know that p must also be even.
- If p is even, it could be expressed as a multiple of two as follows:
- Divide both sides by 2:
WHOA!!!!!
- We now know that
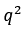 must be an even number. Why? Because it is equal to twice of another number. Remember again...any even number in this world is always a multiple of two.
must be an even number. Why? Because it is equal to twice of another number. Remember again...any even number in this world is always a multiple of two. - We have also now shown that both
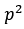 and
and 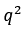 must be even numbers.
must be even numbers.
Whoa...THIS MUST BE A CONTRADICTION OF OUR ORIGINAL ASSUMPTION!
- Remember how we originally assumed we could express
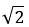 as a ratio of two integers, p and q as follows, with NO COMMON FACTORS between them:
as a ratio of two integers, p and q as follows, with NO COMMON FACTORS between them:
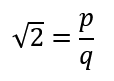
- Yeah, we just showed both
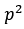 and
and 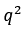 must be even numbers. Even numbers, by design, must be divisible by 2. This means that
must be even numbers. Even numbers, by design, must be divisible by 2. This means that 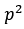 and
and 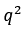 indeed do have common factors.
indeed do have common factors.

- Because the above contradicts our original logic and proves that
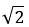 cannot be expressed as a fraction. It is irrational.
cannot be expressed as a fraction. It is irrational.
This fact still amazes me to this day.
The fact that there are infinities of irrationally within our infinities of the real is often hard to grasp. But, its true. It is provable. It is amazing! And, I seriously hope the only drowning I have in common with Hippasus for sharing with the Steemit community is with upvotes.
Now, don't even get me started on the infinities shared with both real and imaginary numbers. Might be a topic for another day ;)
Steemit Board Awards - Click Below for More Information




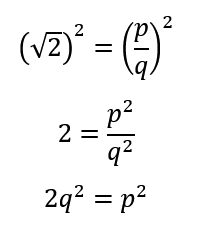
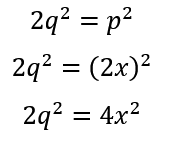
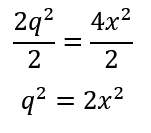

😳 I was good in maths in school and in Engineering but had never given this much thought to irrational numbers. Very nice explanation and a very logical and neatly laid out blog. Thanks for sharing.
Upvoted and followed
I am continuing to focus on my passion, which is wildlife blogs with my original wildlife photos and my musings about them. Have posted a lion cubs life blog today. I request you to take a look if you have time. Your comments would be very welcome.
My favorite complementary theorems in all of mathematics: between every two rational numbers there is an irrational number, and between every two irrational numbers there is a rational number, proving the real numbers are dense.
If Pythagoras found that out:

Haha, yep! Probably would have been burned at the stake or sacrificed in the name of the Gods.
Wohaa! Even i have wrote a blog on pythagoras.. just now. Upvoted. Just go through it. I think, u'll love it. Thanks.
Some really basic prove :P
This post received a 2.4% upvote from @randowhale thanks to @team-leibniz! For more information, click here!
You re really loving math man!
Excellent post :) I heard also from my Computer Science teacher that Pythagoras was scared of beans for whatever reason. I don't know whether I could trust the mathematical theory of a man who is mortally afraid of beans, myself!