Interesting math question
These days when I am preparing the Math exam, I find a very interesting question and I would like to share with you.
Just cut to the chase, the question is,
Q. In how many ways can you make up 200 pence using 10p, 9p, 8p ,7p, 6p, 5p, 4p, 3p, 2p and 1p coins?
I am going to leave you some spaces to think about the question.
Comments
This question is original from a STEP examinations prepare booklet, Advanced Problems in Core Mathematics
, written by Stephen Siklos. And I did some modification so that the question looks more difficult. Here is the original question
Q.Show that you can make up 10 pence in eleven ways using 10p, 5p, 2p and 1p coins.
In how many ways can you make up 20 pence using 20p, 10p, 5p, 2p and 1p coins?
There are varies approach to this problem and the easiest way is to list out all the combination, which I am not going to talk about here.
Another very neat approach is to find the coefficient of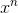 
of the expression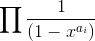 
The booklet don’t explain it at all and I am going to show you the idea of this approach in the following.
First , trivially, the number of ways you can make up n pence using 1p coin is 1, also for the number of ways you can make up kn pence using kp coin, where k is a constant. As the binomial expansion of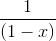 
is 
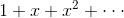
Therefore, the coefficient 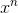of of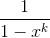 
is equivalent to the number of ways you can make up kn pence using kp coin, 1 if n is multiple of k ,otherwise 0)
Second, so what is the coefficient 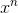of of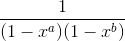 
?By considering 
,
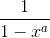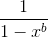in binomial expansion,
=
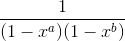and now, the coefficient of 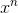is (summation from 0 to n , (coefficient 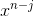of 
of 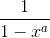) * (coefficient 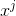of 
of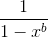 
)). Every summation term is equivalent (number of ways to make up (n-j) pence using ap coin)*(number of ways to make up j pence using bp coin)=(making up n pence using ap and bp coins in one particular way)
Therefore, summing all the terms will add up all possible ways to form n pence, in other words, you get the number of ways to form n pence using ap and bp.
Similar argument will hold for more difference values of coins.
Therefore, the solution of the question would be 1212199424, which is the coefficient 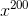of 
of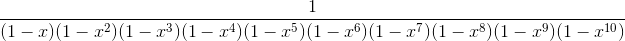 
Here are some advertisement of a online mathematic competition https://steemit.com/cn/@kenchung/-2017623t23429495z, and for the first question , a very neat solution is to sum all the coefficient of
1/((1-x^9)(1-x^10)) before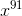 
excluding constant term 1, getting 55.
Thanks for your reading and hope to see you next time.
The STEP question is easy enough, but what level are your students and how much time do you think they would spend on this question?
It's a neat question, assuming the students are at this level.
Hi ,really nice to have a reply 🤗🤗🤗. Actually ,I’m not a teacher ,but a student who took the exam just last week😂😂😂, I got a lot of interesting idea during my preparation and I would like to share them with you😄😄
That's great, fire away!
I often try to encourage my best students to think like examiners or puzzle-makers and create their own questions - few seem able!
This branch of math is called Combinatorial analysis you shoudl read more about generating functios or sequences
Thanks alot, this will be perfect for me to read this summer, waiting for my university offer
Here you can find one of the greates book about it http://algo.inria.fr/flajolet/Publications/AnaCombi/book.pdf it is for free
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by MR.JT from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, theprophet0, and someguy123. The goal is to help Steemit grow by supporting Minnows and creating a social network. Please find us in the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you like what we're doing please upvote this comment so we can continue to build the community account that's supporting all members.