Completing the square
Hello all my friends from the Steemit community, I was away for work reasons, now back I want to share with you a very simple mathematical technique known as square completions that help us solve equations such as:
- Step 1
Adding and subtracting the quotient square (the division / fraction), the coefficient of x between 2
- Step 2
By grouping terms, you will get a perfect square trinomial. The terms x^2 , bx and + b^2/2^2
- Step 3
Factoring (reducing) this trinomial to a squared binomial, which was obtained: (1) extracting the square root of the first term from the trinomial sqrt(x^2) = x, which will be the left-hand side of the binomial; (2) by extracting the square root of the third term from the trinomial sqrt(b^2/2^2) = b/2, which will be the right term of the binomial; (3) using the sign of the second term of the trinomial + bx as the sign separating the terms of the new binomial
Here I leave an example of the application of this technique which is very useful when we just want to clear the variable and not find the roots of the quadratic function.
I hope you enjoy this technique, follow me @falcao12

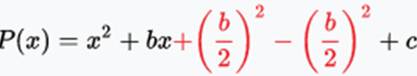

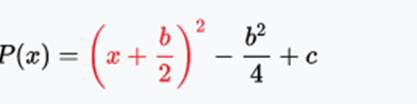

Good to have you back falcao!
Never came across this method actually ^^ good little exercise to get my head around a the logic and usefulness of a new technique :)
Thanks for sharing!
thanks for your comment my friend
i like science and great post my friend
thanks my friend!!
Resteemed your article. This article was resteemed because you are part of the New Steemians project. You can learn more about it here: https://steemit.com/introduceyourself/@gaman/new-steemians-project-launch