Buracos de Minhoca
Quem assistiu a Star Trek
ou o mais recente, Interstellar 1,
tem uma ideia do que são: atalhos no espaço-tempo que permitem aos intrépidos exploradores espaciais cobrir vastas distâncias em pouquíssimo tempo, aparentemente conectando duas regiões afastadas do universo, como nessa representação bidimensional:
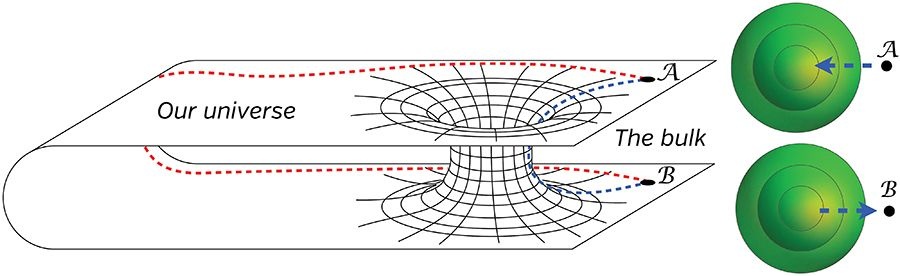
[Fonte: "The Science of Interstellar", de Kip Thorne]
O termo buraco de minhoca ("wormhole", em inglês) foi cunhado por John Wheeler, que também foi o autor de diversos nomes curiosos na física da gravitação, como buracos negros. Nesse caso, ele faz alusão ao túnel que uma minhoca produz numa maçã, conectando duas regiões "distantes" na superfície da maçã:

[Fonte: "The Science of Interstellar", de Kip Thorne]
Mas e estas coisas de fato existem? Ou melhor, vamos tentar responder a uma pergunta muito mais simples: elas são possíveis? A resposta está no final, então aguenta firme.
Karl Schwarzschild [1872-1916] foi um físico e astrônomo alemão, imediatamente famoso por publicar em 1916 a famosa solução das equações de campo de Einstein que descrevem o campo gravitacional exterior de um corpo esfericamente simétrico - como o campo gravitacional do nosso Sol. A solução de Schwarzschild, como ficou conhecida, é uma solução exata (sem aproximações) das equações de Einstein no vácuo
em que tipicamente (em quatro dimensões) os índices i e j assumem quatro valores distintos, 1,2 e 3 para as três coordenadas espaciais, e 4 para a coordenada temporal.
Essas são equações diferenciais para a métrica . Pense na métrica como uma matrix 4x4 simétrica cujas componentes são funções infinitamente diferenciáveis das coordenadas usadas para descrever o espaço-tempo.
O que ela descreve? Um físico lhe dirá que ela descreve a geometria do espaço-tempo, pois se você conhece a métrica, pode calcular a distância (em 4 dimensões) entre dois pontos muito próximos.
Para fixar as idéias, pense num sistema cartesiano em duas dimensões, descrito por um sistema de coordenadas cartesiano , com
sendo o eixo das ordenadas e
sendo o eixo das abscissas. Um ponto nesse sistema será descrito por um par de números: suas coordenadas em relação aos eixos cartesianos. Suponha que esse ponto tenha coordenadas
. Então um ponto muito próximo terá coordenadas
, e a distância ao quadrado entre esses pontos, usando o teorema de pitágoras, será
. É usual representar esse elemento de comprimento quadrático por
. Ou ainda, poderíamos representar o mesmo elemento de comprimento de forma mais compacta, assim:
onde utilizamos a métrica para escrever o elemento, que nesse caso é uma matriz 2x2, já que estamos num espaço com duas dimensões . Comparando as duas expressões, você pode ver que essa matriz é a matriz identidade em duas dimensões:
Agora voltemos à solução de Schwarzschild. A solução, já sabemos, é uma métrica. E essa métrica se escreve da seguinte forma, em termos do elemento de comprimento quadrático,
Nessa expressão, M é a massa da distribuição esfericamente simétrica de matéria (por exemplo, do Sol), e a métrica está dada em coordenadas esféricas, em que r é a coordenada radial, e representa o elemento de ângulo sólido (a parte angular).
O que é interessante observar nesta solução é que a função que multiplica o termo fica singular (o denominador se anula) quando r=0 ou quando r=2M. Essas singularidades podem ter grandes consequências físicas e matemáticas, e em particular, na solução de Schwarzschild, a singularidade r=0 está relacionada à existência de um buraco negro (mas isso é assunto para outro post). A singularidade em r=2M pode ser "removida", entretanto, utilizando um outro sistema de coordenadas que estende aquele inicialmente adotado para descrever a métrica de Schwarzschild. Essa extensão é chamada de extensão de Kruskal, e contem a solução de Schwarzschild.
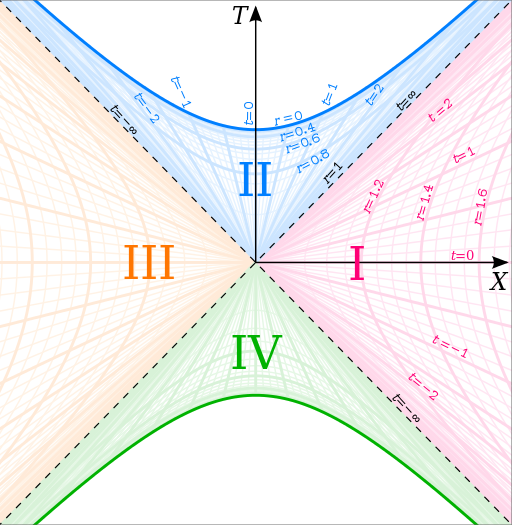
Para representar estas soluções, é comum desenharmos diagramas bidimensionais, em que ignoramos a parte angular. Assim, no diagrama em coordenadas de Kruskal abaixo, cada ponto é uma esfera bidimensional, e possui coordenadas (X,T):
Na figura, a curva r=0 em azul representa a singularidade que mencionei antes, e retas que formam ângulos de 45 graus com a horizontal representam trajetórias de feixes de luz. Se representarmos a hipersuperfície espacial T=0 ( o eixo X) como uma superfície bidimensional imersa num espaço plano em três dimenões, ela teria a forma
Aqui cada círculo é na verdade uma esfera bidimensional (uma coordenada está suprimida). O túnel, ou garganta, conecta as regiões I e III do diagrama de Kruskal, e representa um buraco de minhoca de Schwarzschild, ou ponte de Einstein-Rosen.
Moral da estória: buracos de minhoca são possíveis? Sim, se você aceita que são soluções possíveis das equações de campo de Einstein. Mas aqui entram questões mais complexas, como a estabilidade dessas estruturas, e se é possível atravessá-las em algum sentido. Tenha em mente que este foi só um exemplo simples, e há buracos bem mais complicados na literatura científica (veja, por exemplo, as referências que estão em 2).
Por fim, se você chegou até aqui, aí vai um videozinho para descontrair, o curta "Einstein-Rosen":
ps: como não há suporte nativo para LaTeX, eu acabei me virando com esse workaround.
1Interstellar. Incidentalmente, esse filme recebeu consultoria científica do físico teórico e prêmio Nobel de física Kip Thorne.
2 Wikipedia

Olá, @fresneda : Moito obrigado por o artigo (dame medo ver a humanidade cal virus invadir o universo avanzando a traverso dos buracos de miñoca) e tamén ficamoslle obigados polo recurso aportado para incluir fórmulas nos posts do Steemit.
Este perfil percura posts de calidade relacionados co concepto da galeguia e a equipa de curación decidiu destacar este teu post na publicación O Garimpo: Criar Comunidade, Música, Pecados e Buracos de Minhoca [13/Fevereiro]
Obrigadas pola túa contribución.
Votado e re-steemed
Muito obrigado!
Very well written article