Demostración geométrica del producto (a + b)(a - b)
Saludos cordiales amigos de steemit, mi primera publicación en el área de ciencias y específicamente en matemáticas fue la versión en inglés del artículo "Geometrical demostration of the notable product (a + b)^2" el cual lo reescribí en español para la comunidad hispana a la cual pertenezco. Luego escribí un segundo artículo en la misma línea también en ingles y que se titula: "Geometrical demostration of the product (a +b)(a - b)" y ahora en este post les traigo la versión en español de éste artículo.
El producto denominado suma por diferencia de dos cantidades algebraicas es una útil fórmula del álgebra que usamos mucho en casos de factorización y establece lo siguiente:
(a + b)(a - b) = a^2 - b^2
La demostración de esta igualdad se llevará a cabo usando consideraciones geométricas. Comencemos:
Consideremos dos cuadrados, uno teniendo lados que etiquetaremos con la letra "a" y su área será a^2, y el otro cuadrado tendrá lados etiquetados con la letra "b" y área igual a b^2. (Figura 1).
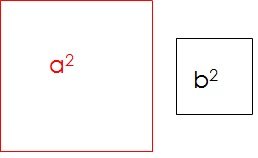
(Figura 1)
Ahora, tomaremos el cuadrado de área b^2 y lo colocaremos sobre el cuadrado de área a^2. (Figura 2).
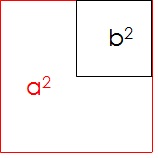
Figura 2
A continuación, dibujaremos una línea recta iniciando en la esquina inferior izquierda del cuadrado de área b^2. Nótese que la línea punteada (Figura 3) tiene una longitud igual a la diferencia entre los lados a y b, es decir, a - b. Por consiguiente, con esta línea tendremos un rectángulo al cual denotaremos con la letra C (en mayúscula, se utilizará letras minúsculas para etiquetar lados). Este rectángulo C tendrá lados (a - b) y b.
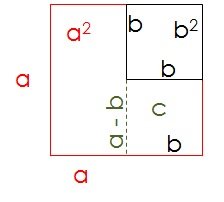
Figura 3
Podemos ver, de la figura 1, una diferencia entre las áreas de los cuadrados y que es mostrado en la Figura 4. La parte pintada en celeste es igual a esta diferencia: a^2 - b^2. También podemos notar que el área del rectángulo C está incluida en la diferencia de áreas a^2 - b^2.
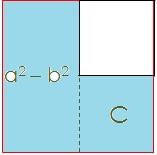
Figura 4
Ahora, si cortamos el rectángulo C y lo colocamos sobre el cuadrado de área a^2 tal y como vemos en la Figura 5, tenemos un nuevo rectángulo con lados (a + b) y (a - b)
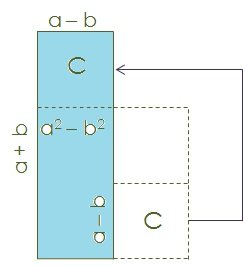
Figura 5
El área de este nuevo rectángulo la obtenemos multiplicando los lados: (a + b) x (a - b) pero esto es igual a la diferencia de áreas a^2 - b^2 el cual está pintado nuevamente de color celeste, por lo tanto de esta forma hemos probado que:
(a + b)(a - b) = a^2 - b^2.
Una vez más hemos obtenido una expresión algebraica a través de la geometría, así de esta manera nuevamente verificamos que la matemática en general se fundamenta sobre bases geométricas.
Referencia: Álgebra, Aurelio Baldor.