Análisis de Estabilidad de Sistemas Materiales Parte III
Saludos y bienvenidos! En esta ocasión, continuando con el estudio de la estabilidad de sistemas materiales en el plano, nos enfocaremos en el análisis de dos tipos de vinculación que pueden presentarse en un sistema material y que pueden llevar el análisis a casos particulares que merecen una revisión detallada: el apoyo simple interno o “patín interno” y el empotramiento libre. En este sentido, se va aportando contenido didáctico dedicado a la Estática Aplicada, rama de la Mecánica que estudia el equilibrio de cuerpos rígidos, en este caso especializada hacia estudios de Ingeniería Civil en donde el estudiante adquiere criterios para discernir en el estado de estabilidad de un sistema material (conjunto de cuerpos rígidos o “chapas”).
Material completo de Estática Aplicada recopilado en la siguiente publicación:
➜Material para Estática Aplicada.
Una vista detallada de las vinculaciones en sistemas materiales se realizó en la publicación Estática Aplicada: los Vínculos y su Aplicación a Sistemas Estructurales en la Realidad en donde se hace mención a todas las posibles formas de vinculación en el plano entre dos chapas o entre una chapa y el “sistema tierra” (sistema de referencia fijo). En la parte I y en la parte II de la presente publicación se estudian sistemas materiales con vinculaciones típicas como lo son las articulaciones fijas, rótulas y apoyos simples, y otras no tan comunes como lo son las bielas paralelas y el empotramiento móvil. Otro par de vinculaciones mucho menos comunes serían el “patín interno” y el empotramiento móvil, por ello se dedica la presente publicación a su análisis.
Introducción
El apoyo simple representa una vinculación de primera especie en la cual solo se restringe una dirección de desplazamiento respecto al sistema tierra. Esta restricción puede ser representada de tres formas diferentes, unas más usuales que otras (Fig. N°1).
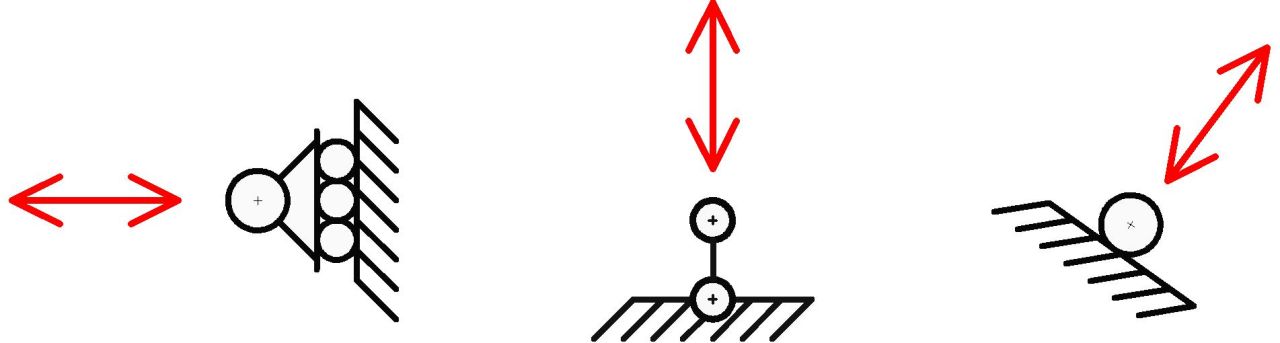
Cuando se convierte esta restricción respecto al sistema tierra a una restricción relativa entre dos chapas podemos llegar a la siguiente imagen gráfica:
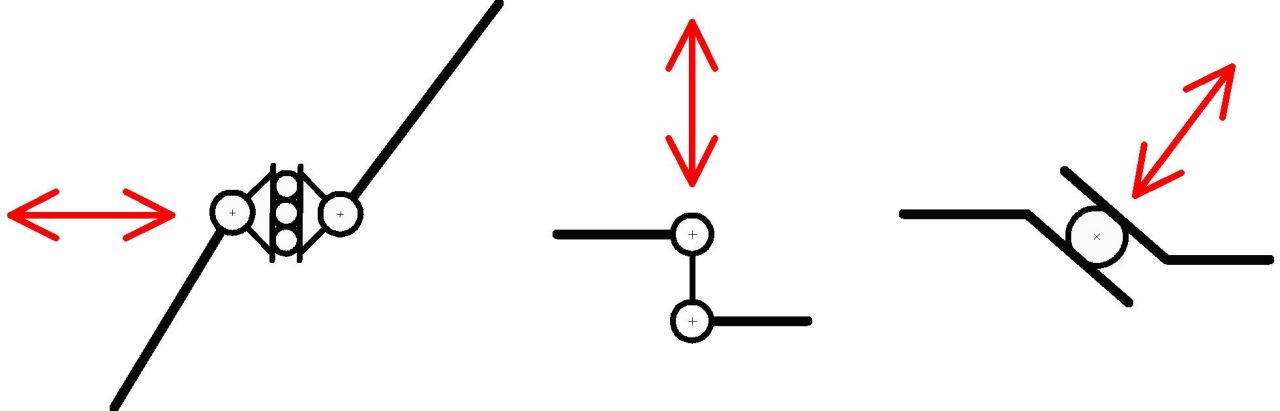
Esta es la vinculación interna cuyo efecto en la estabilidad de un sistema material será analizado. Al solo restringir una dirección de desplazamiento, se observa que solo se aporta 1 unidad de vinculación interna al sistema.
Cuando la única restricción que aporta una vinculación externa es la de rotación, estamos ante la presencia de un empotramiento libre. Su representación gráfica es la siguiente:

Esta vinculación tiene el efecto de anular cualquier rotación respecto al sistema tierra, siendo la traslación la única posibilidad de movimiento que puede ejecutar una chapa vinculada con un empotramiento libre. Cuando se trata de anular la rotación relativa entre dos chapas, nos encontramos con el empotramiento libre interno:

Si bien no tiene sentido que las chapas no estén en contacto directo, esta es la representación gráfica adecuada e indica que ambas chapas pueden desplazarse libremente pero solo si mantienen el mismo ángulo entre ellas (rotación relativa impedida).
Al ser todas estas vinculaciones de primera especie, no brindan por si solas la ubicación del polo absoluto o relativo, en el caso del apoyo simple interno, solo brinda una dirección sobre la cual se encontraría el polo relativo, y para el empotramiento libre sabemos que el polo estará en el infinito pero no conocemos su dirección.
Al igual que en las primeras dos publicaciones disponemos de las siguientes herramientas y teoría para ejecutar el análisis de estabilidad de un sistema material:
Mediante la Ecuación (3) del artículo Determinación Algebraica de los Grados de Libertad de Sistemas Materiales en Estática Aplicada y Ejemplo de Aplicación podemos determinar los grados de libertad de un sistema material:

Donde “n” representa el número de chapas, “Vext” y “Vint” la cantidad de unidades de vinculación externas e internas respectivamente. Pero el número obtenido mediante la ecuación (1) debe ser verificado mediante un análisis geométrico de posibles polos en el sistema, ya que esta ecuación no advierte sobre la existencia de vínculos aparentes que no introducen restricción alguna.
El Teorema de Kennedy o teoremas de los polos, indica que el alineamiento de los polos absolutos y relativos de un sistema material establece la presencia de una cadena cinemática de 1 grado de libertad, sistema que es inestable. Se considera suficiente la verificación del primer teorema de los polos (1mer TDP), relacionado a los polos absolutos:

Tal como se mencionó en la Parte I de la presente publicación, se pueden presentar tres situaciones luego de aplicar el 1mer TDP:
Ejemplos de Análisis de Estabilidad de Sistemas Materiales
Ejemplo N°1: caracterizar el comportamiento inestable del siguiente sistema material de 1 grado de libertad.
En el siguiente sistema material, analizaremos el efecto de los vínculos antes mencionados (patín interno y empotramiento libre) sobre la estabilidad del mismo.
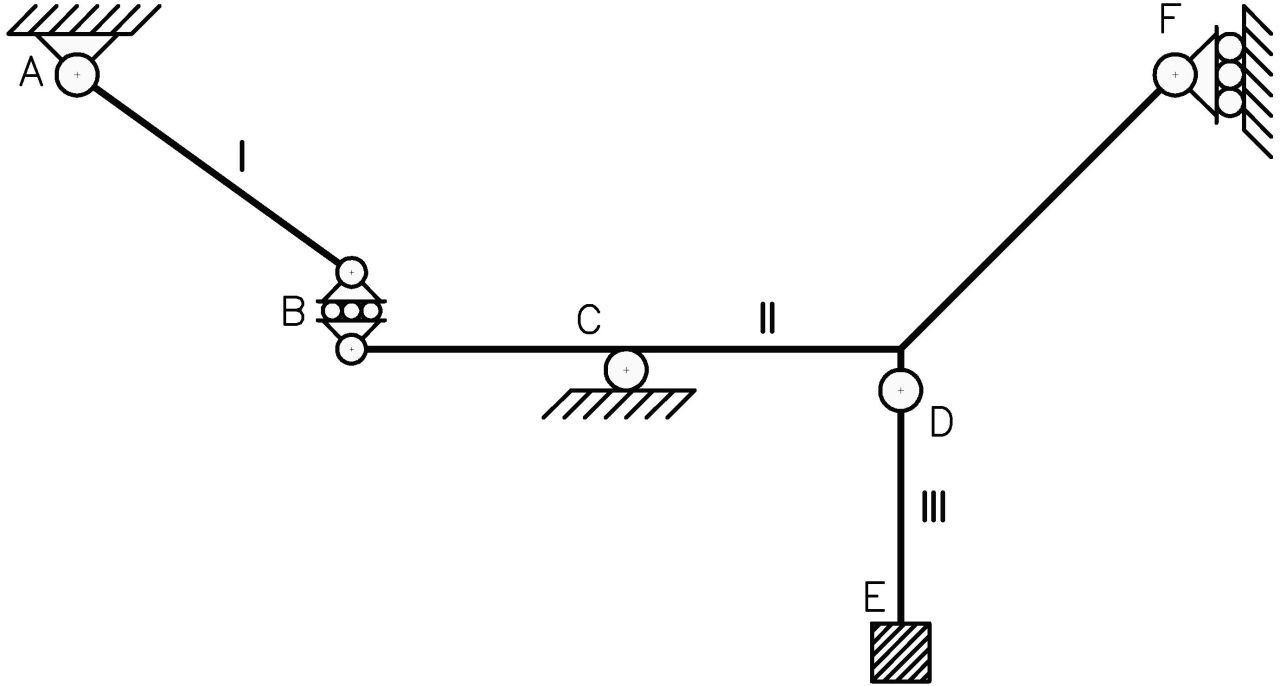
Se sabe que el sistema presenta 1 grado de libertad, sin embargo a modo de comprobación se totalizará el número de chapas, vinculaciones externas y vinculaciones internas para determinar los grados de libertad según la ecuación (1):
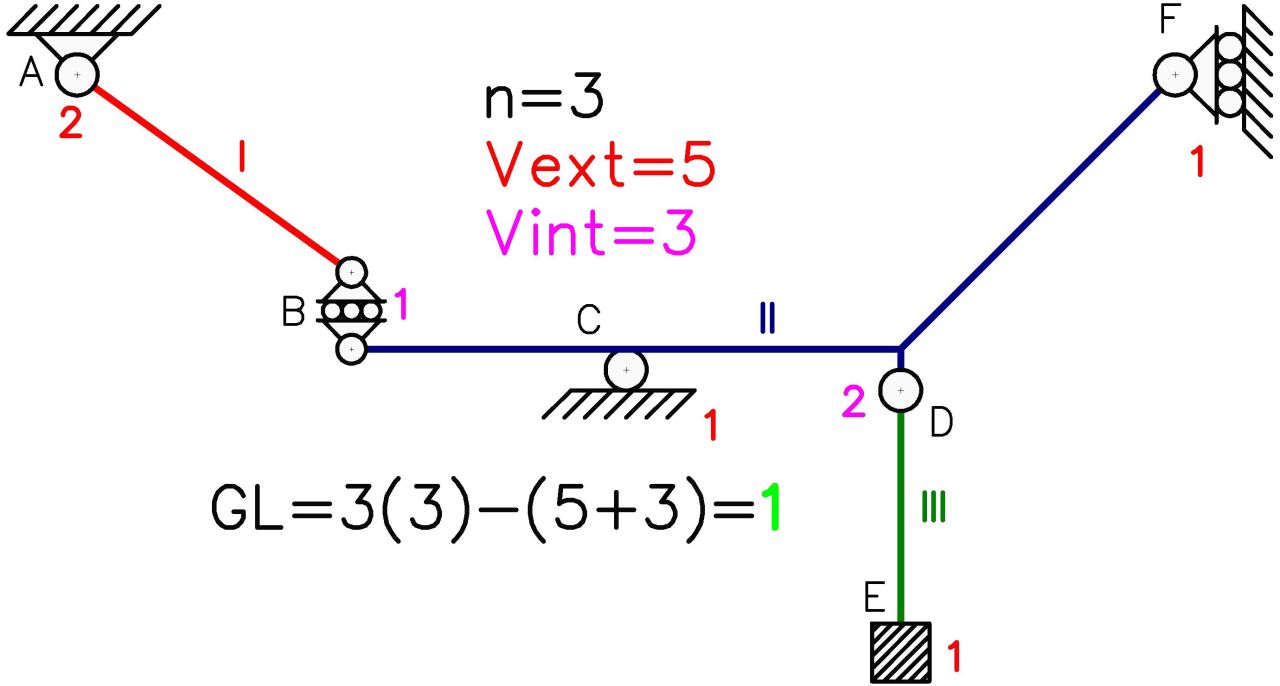
Esto por lo tanto, indica que se cumple el Teorema de Kennedy (primer teorema de los polos) en el sistema material. Se presenta la posibilidad de hallar una solución única para los polos absolutos y relativos de la cadena cinemática de 1 grado de libertad presente en el sistema.
El comportamiento inestable viene dado por la presencia de una cadena cinemática de 1 grado de libertad, en la cual el movimiento de sus puntos viene siendo dependiente de un centro instantáneo de rotación único.
Para proceder a caracterizar el comportamiento inestable del sistema material vamos a hallar la ubicación del centro instantáneo de rotación (polo absoluto) de cada una de las chapas de la cadena cinemática, así como también los polos relativos entre ellas.
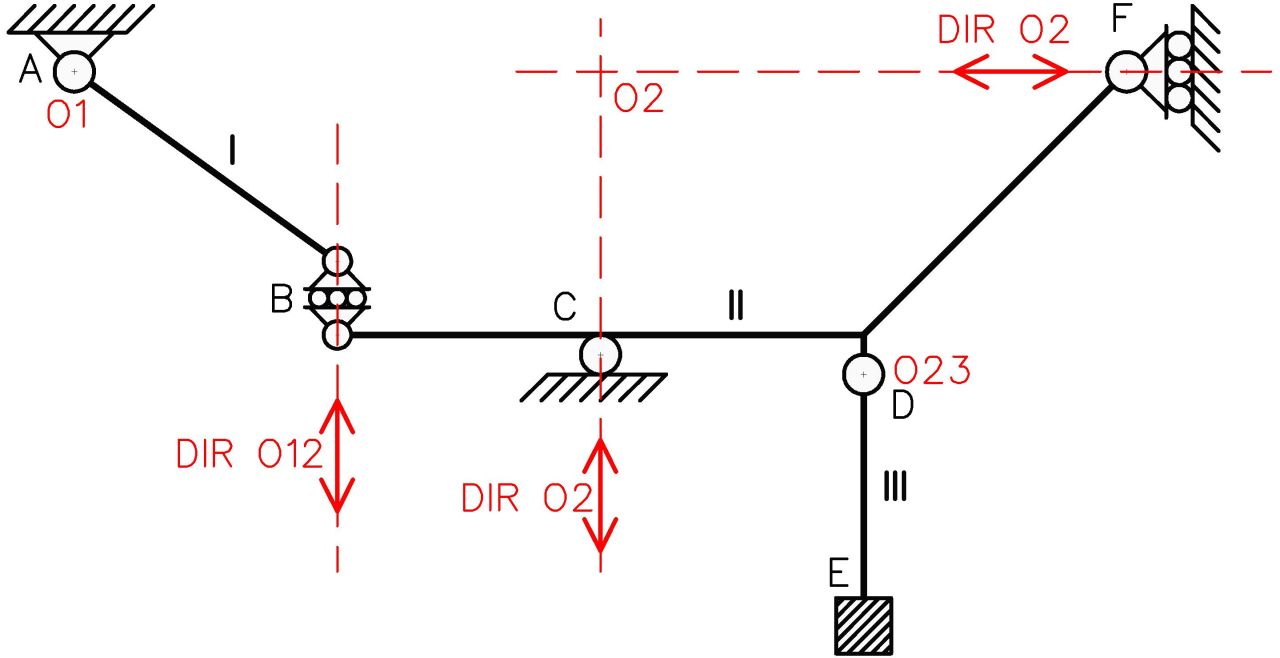
En la Figura N°7 se han hallado los polos absolutos y relativos en función de las restricciones que aportan los vínculos existentes. Se observa que el polo O2 fue hallado por la intersección de las direcciones dadas por los apoyos simples ubicados en C y F. Aún no se posee la información suficiente para hallar la ubicación del polo absoluto de la chapa III ni tampoco la del polo relativo O12. Recordemos que el “patín interno” es un vínculo interno de primera especie, y nos brinda una dirección para la ubicación del polo relativo mas no la ubicación exacta.
Como ya sabemos, el sistema posee 1 grado de libertad por lo que la ubicación de los polos restantes se encontrará en la alineación de los polos absolutos con el relativo entre dos chapas (1mer TDP). Aplicaremos el 1mer TDP para hallar la ubicación de los polos aún desconocidos:
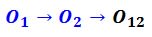
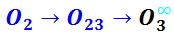
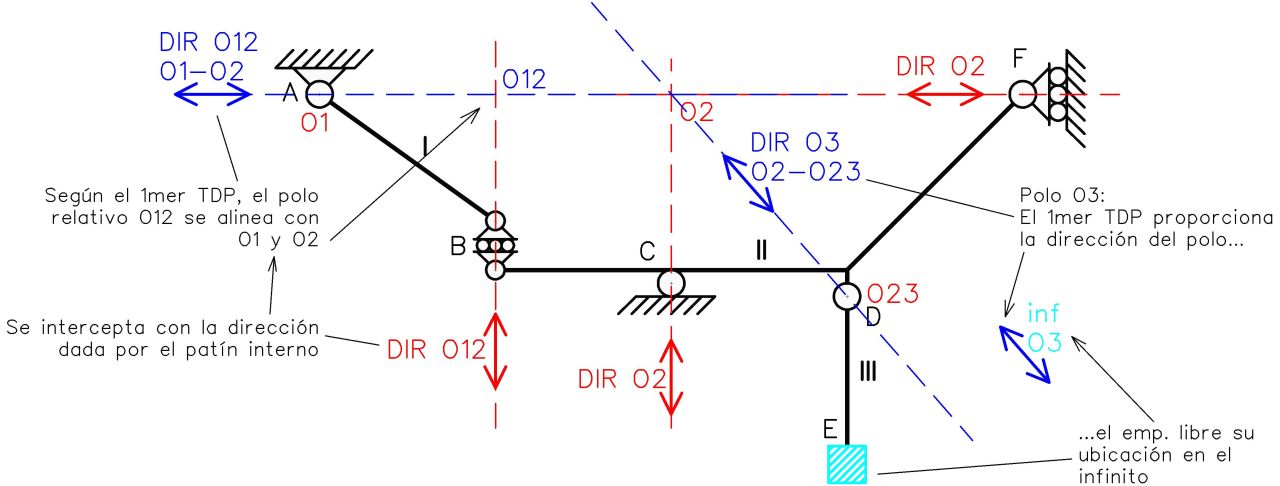
Como hemos observado en la figura N°8, la ubicación del polo O3 se halló trazando la dirección dada por el 1mer TDP (alineación de O2 con O23) esto nos proporciona la dirección en la que el polo O3 se encuentra hacia el infinito. Recordemos que el empotramiento libre en E nos indica que la chapa III no puede rotar sino solo trasladarse, lo cual ya nos dice previamente que su polo absoluto debe de estar en el infinito y solo se necesita una dirección para conocer su ubicación exacta.
El polo relativo O12 se debe encontrar alineado entre O1 y O2 tal como lo indica el 1mer TDP, esta dirección de intercepta con la dirección brindada por el patín interno en B para encontrar la ubicación de O12.
Ya hemos identificado los polos absolutos y relativos del sistema. Podemos caracterizar entonces el comportamiento del sistema, el cual indica que las chapas I y II rotarán alrededor de sus polos absolutos respectivos, siendo el polo relativo O12 el punto donde se encontraría una rótula si ambas chapas se extendieran hasta el mismo. La chapa III se trasladará perpendicular a la dirección de su polo en el infinito, y en una magnitud proporcional a la magnitud de la rotación de la chapa III.
Una vez identificado el comportamiento inestable surge la siguiente pregunta:
¿Cómo se mueve el sistema y cuál es el efecto del patín interno y el empotramiento libre?A través del siguiente GIF podemos observar los desplazamientos de los puntos del sistema donde el movimiento de la cadena cinemática se presenta de manera bilateral. Se observa que el patín interno mantiene su restricción relativa en dirección vertical mientras permite desplazamientos relativos de dirección horizontal. La chapa III solo se traslada. Se asume que el movimiento es de orden infinitesimal por lo que la ubicación de los polos absolutos no cambia.
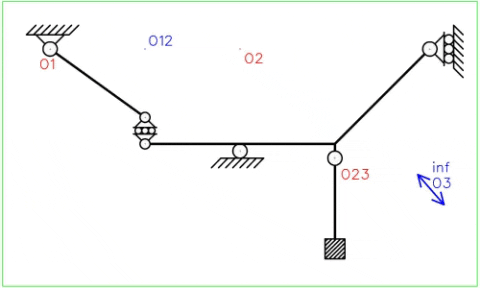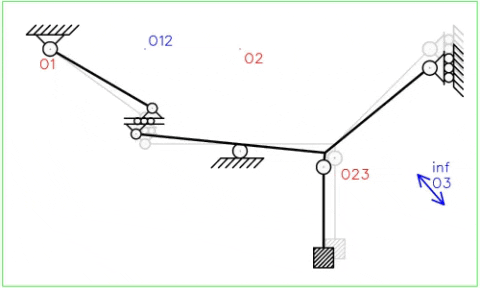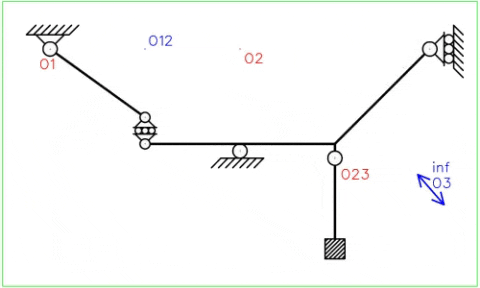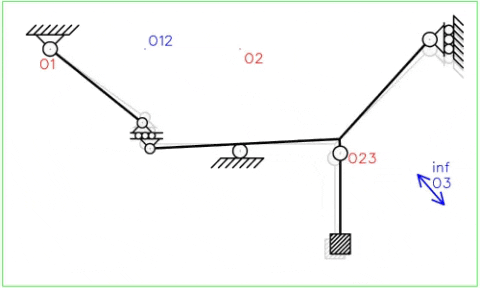
La principal diferencia entre el apoyo simple interno y las bielas paralelas es que estas últimas no se permite la rotación relativa entre chapas, haciendo que de esta manera no puedan rotar de manera independiente sino que cada chapa debe rotar de manera similar a la otra. Se observa en la Fig. N°9 que el apoyo simple interno permite que ambas chapas roten de manera independiente.
Ya vemos como el empotramiento libre influye en el movimiento de una cadena cinemática de 1 grado de libertad, pero ahora veremos cómo este vínculo externo puede llegar a convertirse en un vínculo aparente.
Ejemplo N°2: verificar si el empotramiento libre en C representa un vínculo aparente.
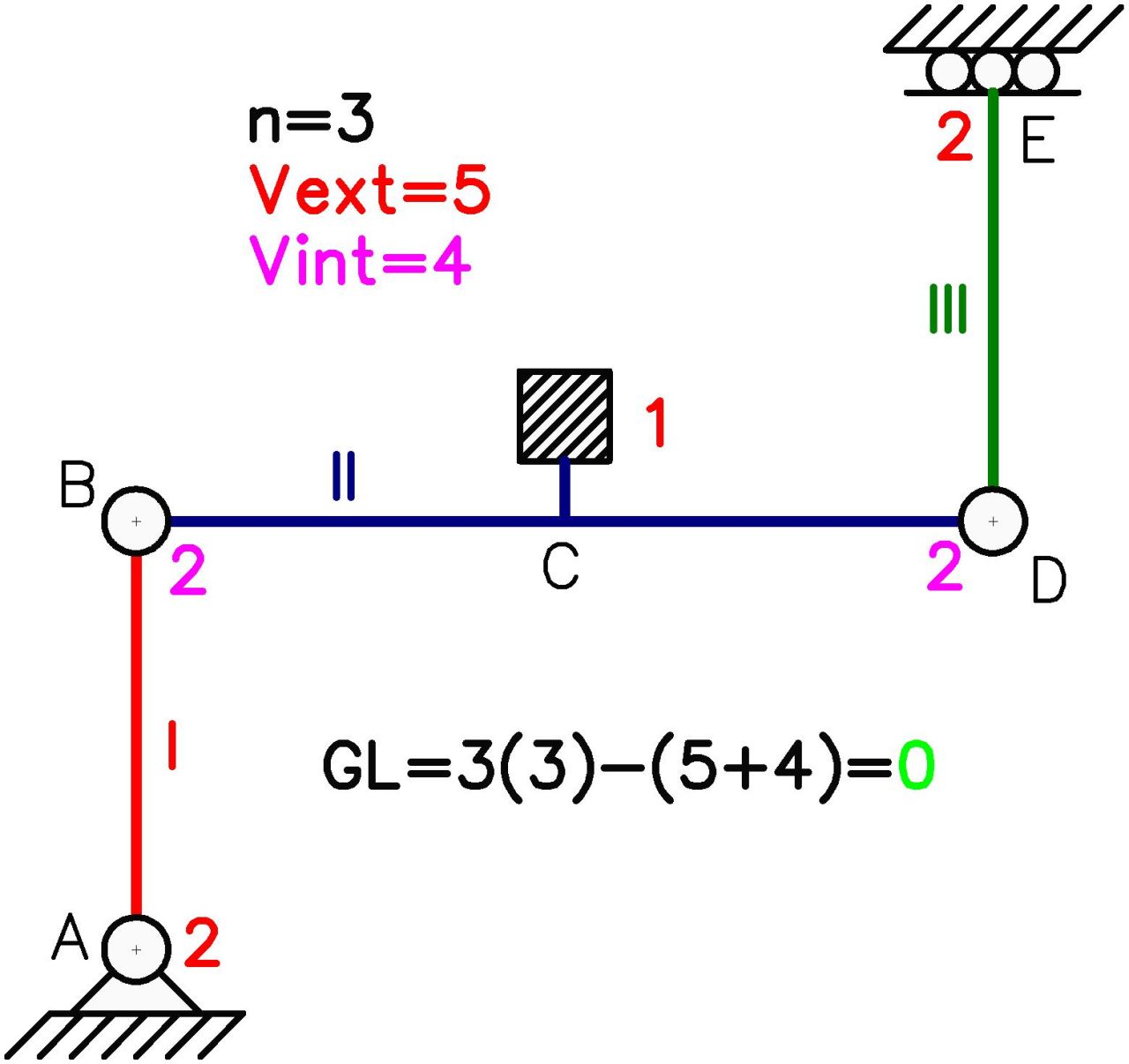
Podemos observar como la ecuación (1) refleja que el sistema posee 0 grados de libertad, por lo que tendría las vinculaciones suficientes para ser estable, lo cual comprobaremos mediante un análisis geométrico de polos en el sistema.
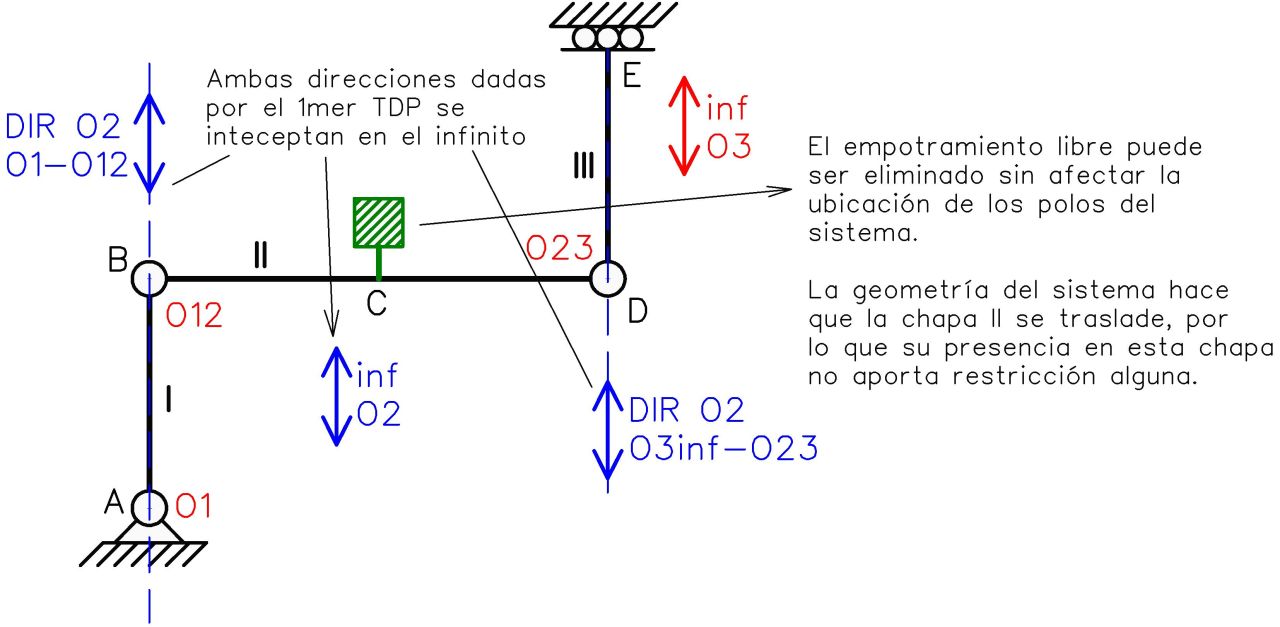
En la Fig. N°11, al hallar los polos del sistema que proporcionan los vínculos ya existentes (en rojo) no encontramos que solo nos queda por hallar el polo absoluto de la chapa II. Al aplicar el 1mer TDP en todo el sistema (en azul) para establecer la posible ubicación del polo O2, tenemos que las direcciones dadas (O1-O12 y O3inf-O23) se interceptan en el infinito, brindando así la ubicación del polo O2.
Todo lo anterior se ha podido hacer sin necesidad de realizar análisis alguno sobre el empotramiento libre en C. Es decir, el efecto de este vínculo es hacer que la chapa II no pueda rotar sino trasladarse, pero la geometría del sistema ya de por sí hace que esta chapa se traslade por lo que la presencia de este vínculo no aporta restricción alguna sobre esta chapa y puede ser removido sin afectar el comportamiento del sistema.
Al existir solución única para el polo absoluto de cada chapa se confirma que el sistema material es una cadena cinemática de 1 grado de libertad y que el vínculo aparente puede ser representado por el empotramiento libre en C. Recordemos que no existe solución única para el vínculo aparente, y en este ejemplo se ha hecho énfasis en la restricción aparente del empotramiento libre.
El empotramiento libre es un vínculo externo de primera especie, aporta una unidad de vinculación la cual es representada por la restricción de rotación que ofrece. También puede darse la posibilidad de encontrar el “empotramiento libre interno” el cual sería lo mismo que el anterior pero restringe la rotación relativa entre dos chapas. A través del siguiente ejemplo le daremos una breve revisión al efecto de este vínculo interno a comportamiento inestable de un sistema.
Ejemplo N°3: analizar el efecto del empotramiento libre interno en el sistema.
El siguiente sistema material presenta 1 grado de libertad por lo que se cumple el 1mer TDP en el mismo. Se puede hallar fácilmente la ubicación de los polos absolutos de ambas chapas.
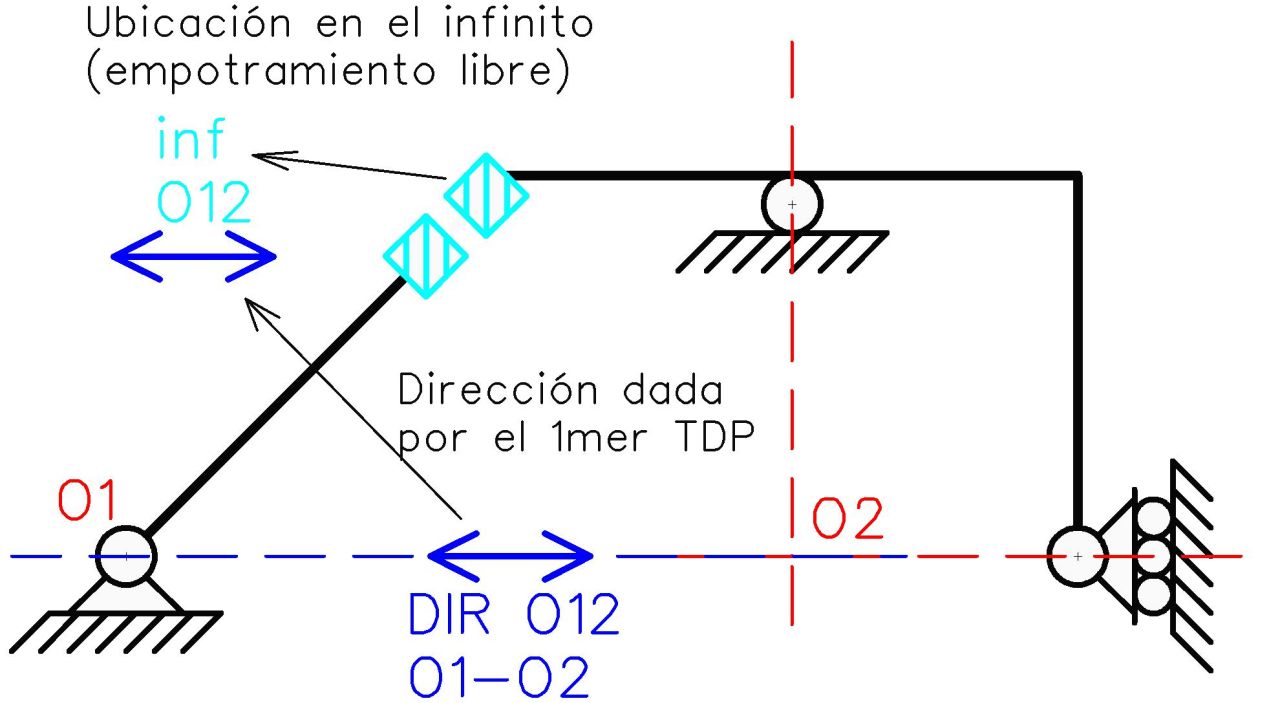
La ubicación del polo relativo se establece mediante el 1mer TDP, puesto que se encuentra alineado con O1 y O2. Tal como sucede con el empotramiento libre externo, la ubicación en el infinito es establecida por el mismo vínculo al no permitir rotación relativa, y su dirección es definida por la dirección dada por el 1mer TDP.
El comportamiento del sistema viene dado por la rotación de las chapas I y II alrededor de sus respectivos polos absolutos. El efecto del empotramiento libre interno se hace notar por la restricción de toda rotación relativa (polo relativo en el infinito), por lo que ambas chapas están destinadas a rotar en el mismo sentido y en igual magnitud. Es decir, si la chapa I rota “α” en sentido anti horario, la chapa II también lo hará.
Ahora veremos un caso particular entre dos chapas vinculadas por un patín interno, en el cual una de ellas no puede moverse.
Ejemplo N°4: analizar la estabilidad del siguiente sistema material.
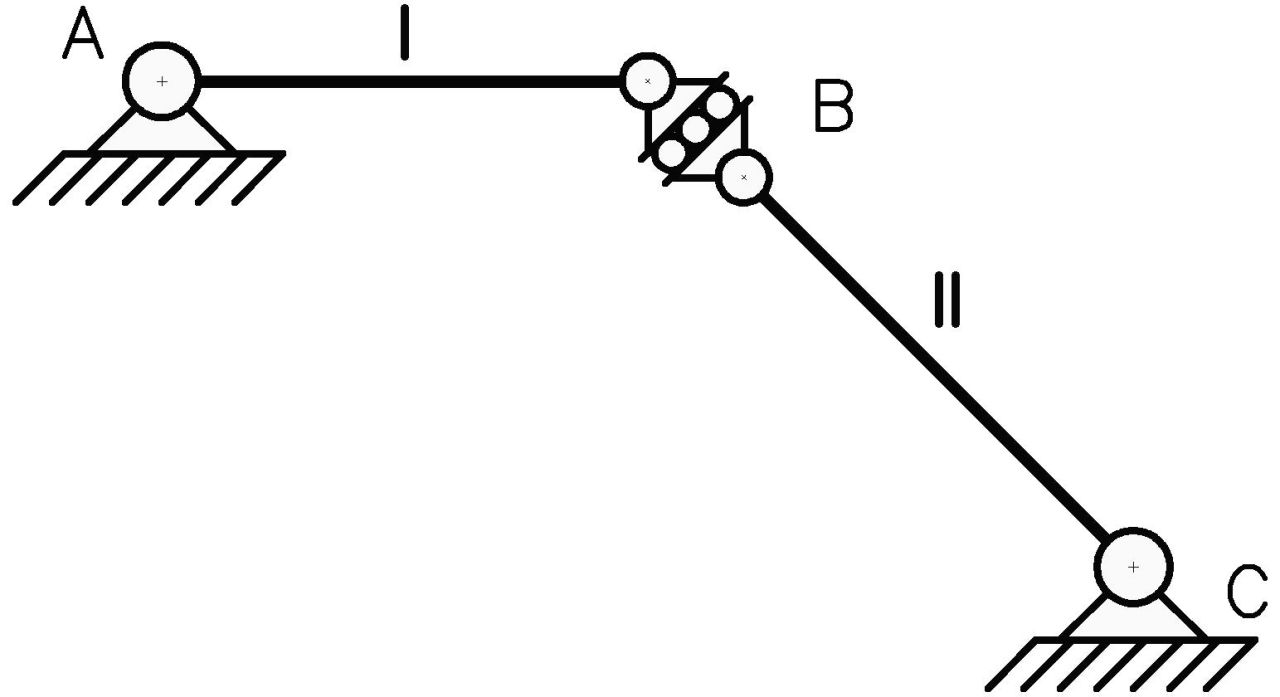
Tal como se observa, disponemos de 4 unidades de vinculación externas (2 por cada articulación a tierra), 1 unidad de vinculación interna (patín interno en B), y 2 chapas. Al aplicar la ecuación (1):
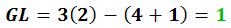
Se determina que el sistema posee un grado de libertad. Se procede a hallar la ubicación de polos absolutos y relativos para comprobar el cumplimiento del 1mer TDP:
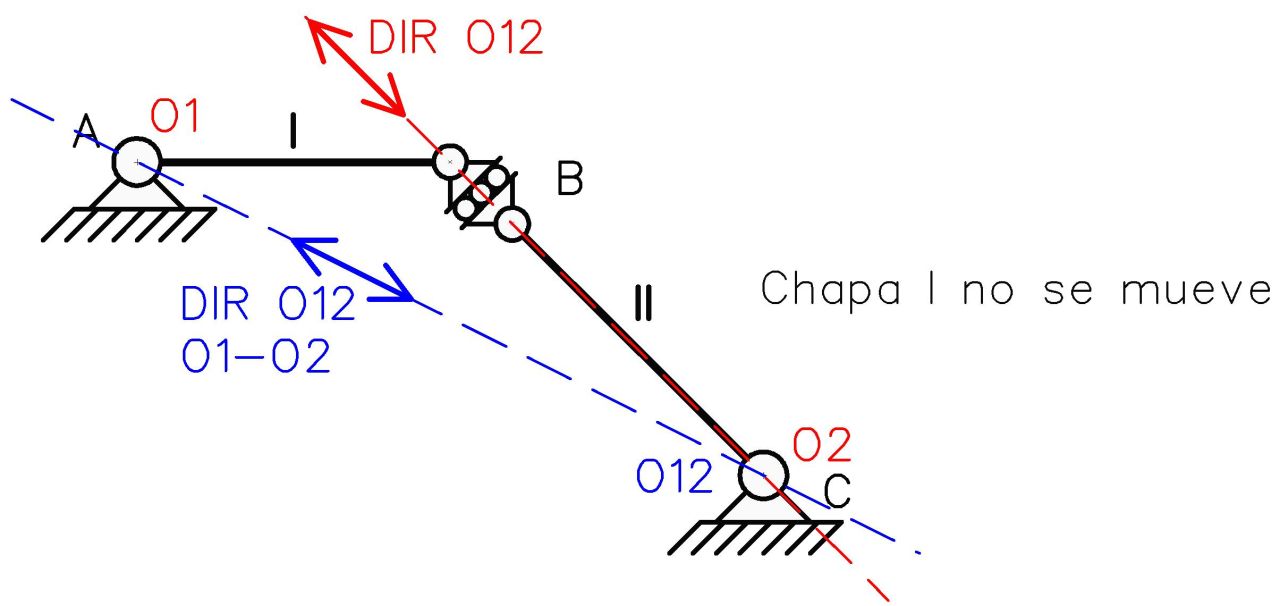
Observamos previo a la aplicación del 1mer TDP (en rojo) que aún no se conoce la ubicación del polo relativo O12 sino una dirección proporcionada por el patín interno en B. Para hallar este polo relativo se procede a trazar una dirección dada por el 1mer TDP (O1-O2 en azul) en la cual debe encontrarse este polo relativo para el cumplimiento de este teorema. Ambas direcciones dadas se interceptan en el punto C, justo donde se encuentra el polo absoluto O2.
Ya obtenidos todos los polos absolutos y relativos se puede concluir que el sistema posee 1 grado de libertad ya que se cumple el 1mer TDP y no hay vínculos aparentes. Además la chapa I no se mueve y el movimiento del sistema solo viene dado por la rotación de la chapa II.
Seguramente surge la pregunta:
¿Por qué la chapa I no se mueve?
Para responder esto, debemos pensar en el polo relativo como el punto donde ambas chapas se vincularían mediante una rótula si ambas se extendieran hasta el mismo. Si hacemos esto en el sistema mostrado, encontramos que esta “rótula ficticia” coincidiría con la articulación fija a tierra en C (Fig. N°15).
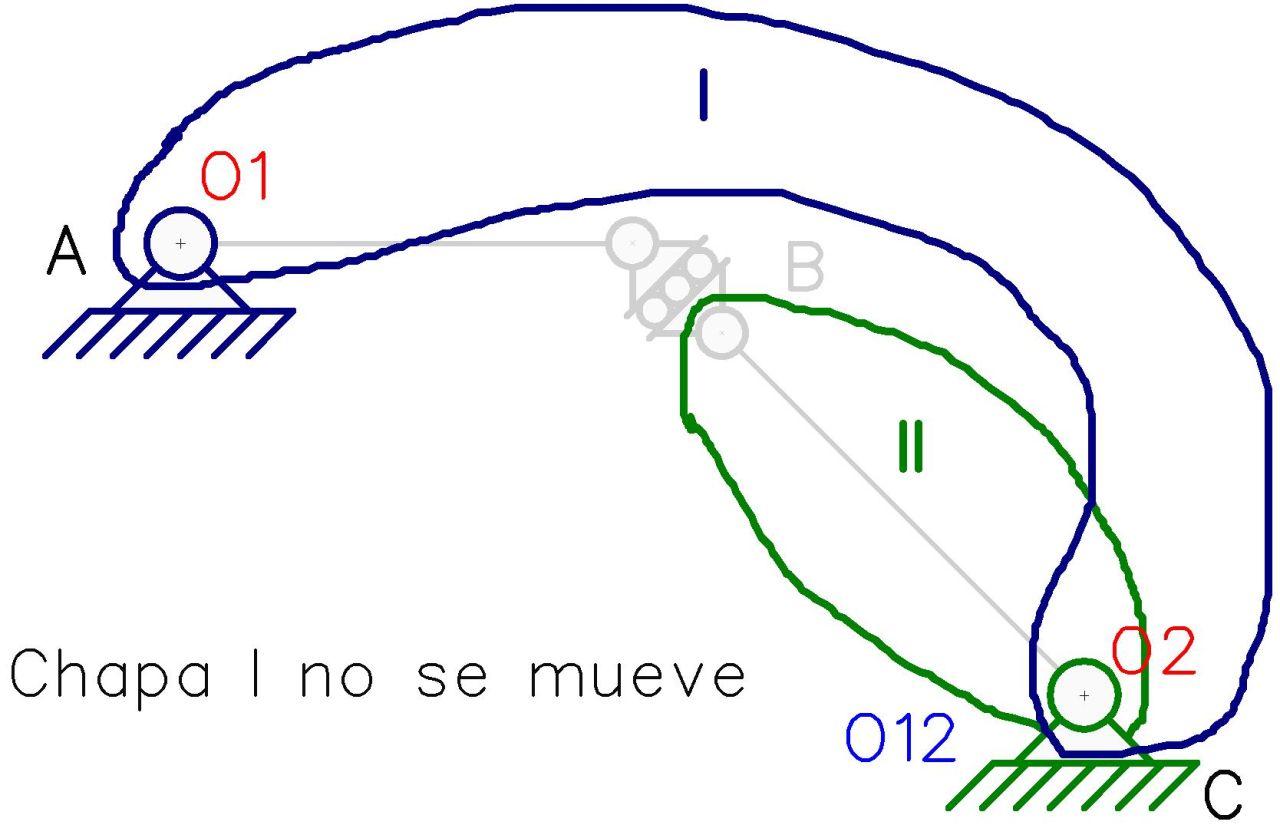
Se observa claramente en la Fig. N°15 como la chapa I está articulada a tierra en dos puntos diferentes por lo que esta no puede moverse, mientras que la chapa II es libre de rotar alrededor del punto C.
Otra forma de simplificar el análisis de esta vinculación interna es sustituirla por otra vinculación equivalente: la biela simple (Fig. N°16). Si bien los vínculos son de tamaño infinitesimal y su forma es meramente representativa, podemos perfectamente asumir que la biela simple es otra chapa más del sistema, y además se introducirían dos rótulas (B y B’) que articulan esta “nueva chapa” con las ya existentes.
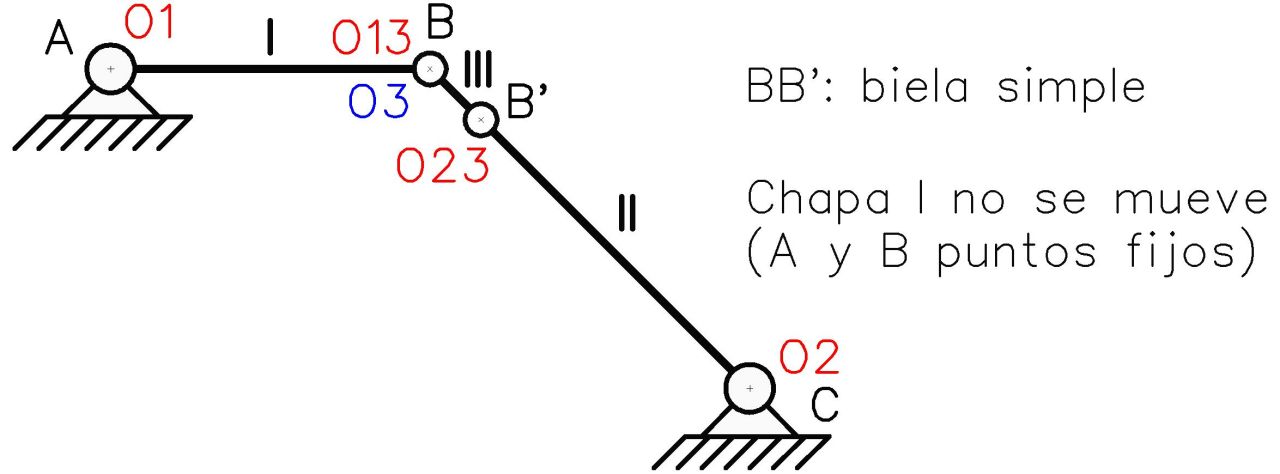
Al encontrar los polos del sistema mediante el 1mer TDP, encontramos que el polo de la biela simple se encuentra coincidiendo con el punto B, por lo que de nuevo la chapa I presenta dos puntos fijos (A y B) imposibilitando su movimiento. El movimiento del sistema viene dado por el posible desplazamiento del punto B’ en dirección perpendicular al radio vector que une el polo absoluto (tanto de II como de la biela simple) con dicho punto.
Conclusiones
Referencias Bibliográficas
Material recomendado
Imágenes y ecuaciones de autoría propia realizadas mediante LibreCAD y Microsoft Word por @acont. Gif creado mediante Giphy.com.
Material completo de Estática Aplicada.
Saludos @acont. Estás invitado a participar en nuestra comunidad científica, tus aportes pueden servir a nuestros usuarios y esperamos contar con una minipresentación de tus áreas de conocimiento.
Puedes visitarnos en: https://discord.gg/Sx8kS8
Recibido @iamphysical, estaré pendiente del canal de Discord de stem-espanol.
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie.
If you appreciate the work we are doing, then consider supporting our witness stem.witness. Additional witness support to the curie witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for having added @steemstem as a beneficiary to your post. This granted you a stronger support from SteemSTEM.
Thanks for having used the steemstem.io app. You got a stronger support!
Congratulations @acont! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
You can view your badges on your Steem Board and compare to others on the Steem Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Vote for @Steemitboard as a witness to get one more award and increased upvotes!
¡Buen trabajo! Te sugiero dividir en varias publicaciones el contenido porque es bastante interesante, pero extenso! Buena diagramación y dominio.. Felicitaciones
Gracias @alexaivytorres, lo tendré en cuenta para el futuro, no es la primera vez que me lo comentan, es que me inspiro mucho con esta materia jaja
Excelente!
Me hiciste recordar los días en los cuales estudiaba ingeniería jajaja tiempos aquellos, gracias por el aporte.