Two Squares in a Circle Problem

---

I came across this interesting geometrical problem the other day. The problem uses only secondary school algebra and geometry, but it stumped some Stanford graduate. For me, it took me 15 minutes to figure out.

The Problem

We have a big square inscribed within a circle, and a smaller square, incribed in one of the spaces between the big square and the circle, as shown in the diagram. The question is: what is the exact ratio of the radius of the circle to the length of a side of the smaller square?

---

The Struggle

Think!
.
.
.
think
.
.
.
think
.
.
.
Let r be the radius of the circle.
Let s be the length of a side of the smaller square.
The question is about finding r : s, or equivalently, .
.
.
.
think
.
.
.
think
.
.
.
think
.
.
.
maybe we can form some equations
.
.
.
think
.
.
.
think
.
.
.
what do we know? the corner of the large square exactly touches the circle ... kind of helpful, eh? but how so?
.
.
.
think
.
.
.
think
.
.
.

The Solution, Stage 1

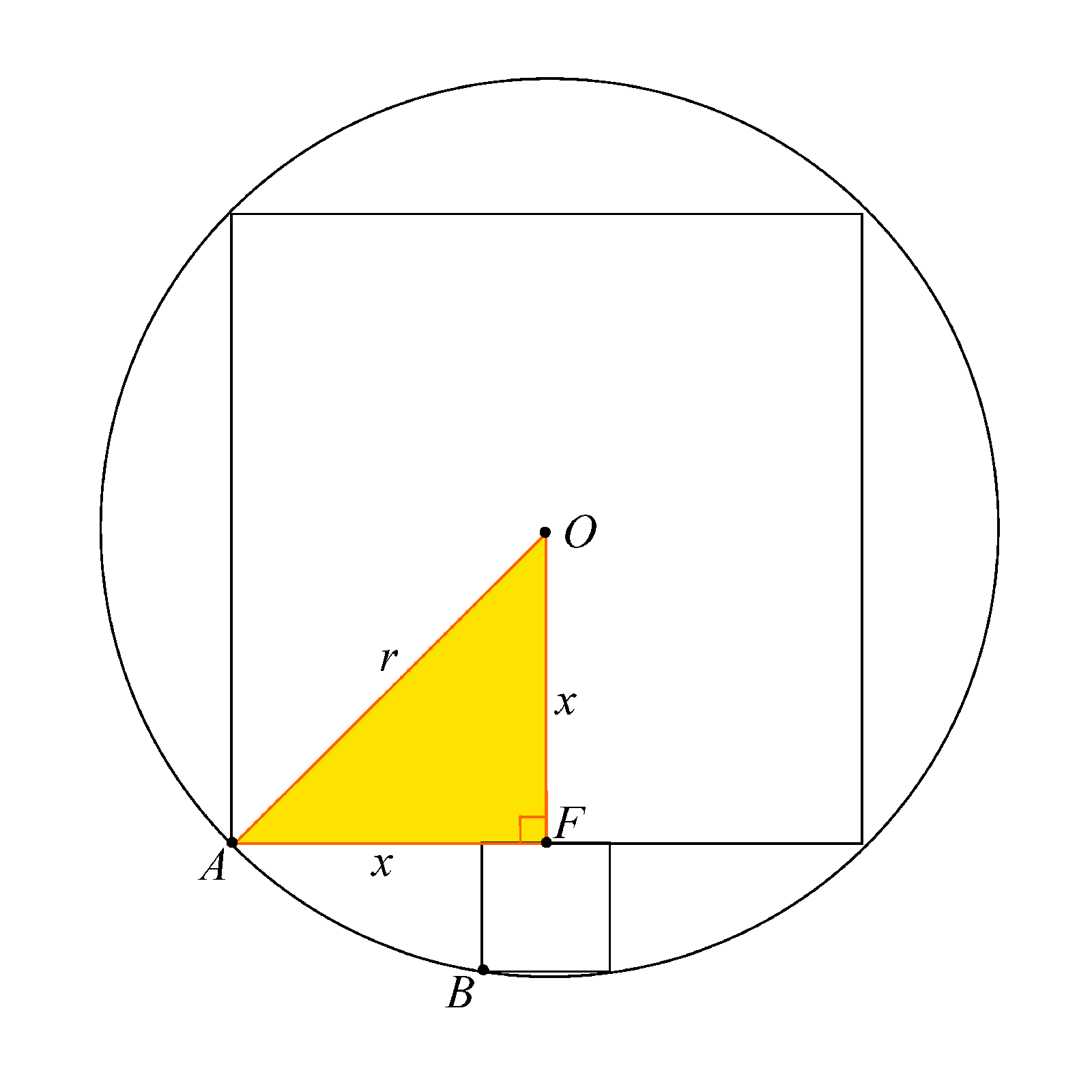
We can drop a perpendicular from the centre O to one of the sides, we call F the foot of the perpendicular and we label one of the corners of the large square as A. See the diagram below.

From symmetry, we can figure out that angle OAF is 45 degrees and/or that OF = AF = x (say). From our earlier definition, we have OA = r. Since we have a right-angled triangle OFC (coloured in orange), we can apply Pythagoras' Theorem.

Solving that, we find that , rejecting the negative root, since we are dealing with lengths.

OK, we got part of the problem solved. Solving part of the problem is one of the heuristics recommended by Singapore's Ministry of Education for solving mathematical problem. Yes, but how do we solve the whole problem?

The Solution, Stage 2

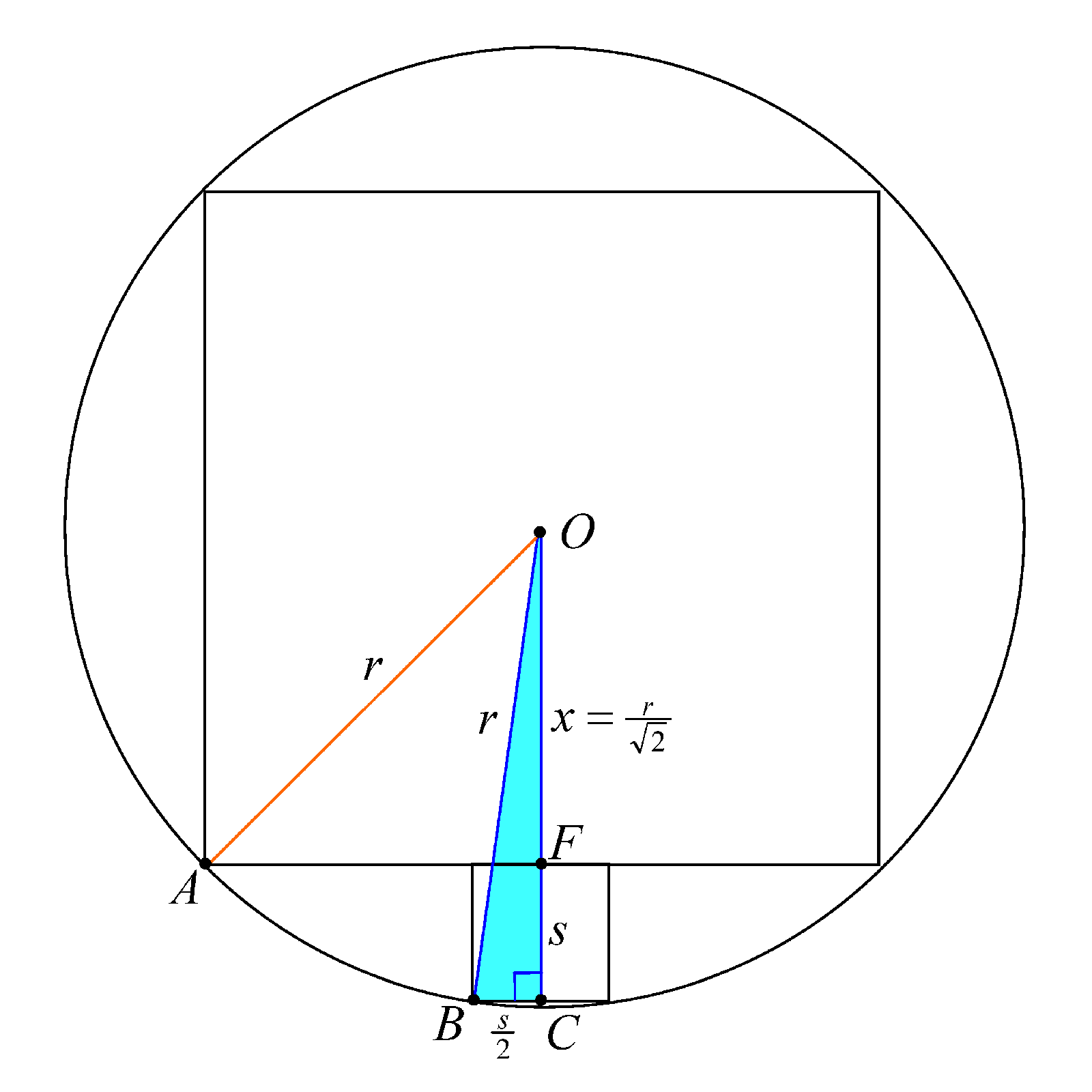
We notice that two corners of the small square also just touche the circle. We label one of these corners as B. We can produce (extend) OF to touch the other side of the square at a point C (say). See the diagram below.

We know that OF = x = , FC = s, and BC = . We have another right-angled triangle OBC (coloured in light blue), and so we can apply Pythagoras' Theorem again.

After 3 lines of manipulation, we arrive at an equation with r² and s². But since we want the ratio r / s, we divide through by s² and treat r / s as if it is one entity. Applying the quadratic formula, and rejecting the "minus" answer, we get . In other words, r : s = : 2.

Reflections

I have shown you the process of solving a challenging mathematical problem. What is needed to solve this problem successfully?

Solve part of the problem. e.g. I found x which is half of the length of the large square. This was useful later.

We need to make observations. e.g. that the corners of the large square and some corners of the small square touch the circle.

We need to translate the observations into mathematical equations. e.g. the use of Pythagoras' Theorem twice.

Note that we do not need to know the individual values of r and of s in order to solve for their ratio. By treating r/s as one thing, we make it unnecessary to solve them individually, which would be impossible anyway. Why impossible? That is because it is possible to have the same situation with an enlarged or shrunken diagram and thus have different values of r and of s. However, the ratio r/s will be the same, because we would solve the same quadratic equation and get the same answer.

Remember to keep cool and calm. If your brain is too excited, the signals in your brain get jammed, and you would not be able to think clearly, or get in touch with your intuition. However, some relaxation (but not too much) helps to keep your mind at an optimal state.

I hope you have learned something from this article.

---

Copyright
All the images in this article are my own original work.

---

Announcements

You might also want to read my recent articles:
"Singapore Math" : The Cows and Goats Problem
Inequality: Always, sometimes or never?

If you find my articles useful or interesting, please upvote and resteem them! Thanks !

Cheers!!!

@tradersharpe
-- promoting sharp minds