Ciencia de Materiales: Parámetros de la red cristalina y curva universal en semiconductores
Parámetros de la red cristalina y curva universal.
Giovanni Marín
Fuente: Archytas curve
Saludos mis estimados amigos de la comunidad científica #stem-espanol
Comienzo mi publicación mostrando una imagen de la curva de Arquitas, matemático griego que utilizó sus conocimientos en aplicaciones técnicas y formuló la utilización de algoritmos generales para la intersección de superficies simples y cuadráticas, así que me plantee la hipótesis de construir una curva universal usando los parámetros de la red cristalina de semiconductores ternarios normales y los compuestos con vacancias de cationes [R1].
La misma estructura cristalina: Calcopirita
El indexado de los picos registrados en el patrón de difracción de rayos X de todos los Compuestos con Vacancias de Cationes, generan como única solución la correspondiente al sistema tetragonal relacionado con la estructura calcopirita, en contraste con lo reportado por otros investigadores que obtienen estructura estanita, cúbica y hexagonal.
El refinamiento de los datos de difracción se corresponde muy bien con el grupo espacial  y que yo he propuesto como condición inicial que tengan una estructura calcopirita de cualquier grupo espacial, perteneciente al sistema tetragonal para garantizar que tengan características similares para formar parte de la curva universal.
y que yo he propuesto como condición inicial que tengan una estructura calcopirita de cualquier grupo espacial, perteneciente al sistema tetragonal para garantizar que tengan características similares para formar parte de la curva universal.
Definición de variables.
Para analizar la influencia de los pares de defectos donador-aceptor (PDDA) sobre la estructura cristalina en los compuestos ternarios ricos en In o Ga en los sistemas Cu-In(Ga)-Se(Te), se ha definido el parámetro m que representa la fracción de la vacancia de catión sobre el número total de cationes. En el caso de los CDO de la familia Cu-III3-VI5 existe una (1) vacancia en los cinco (5) cationes que debería tener la fórmula química, por lo tanto, m = 1/5 = 0.20. En los compuestos de la familia I-III-VI2, no se tienen vacancias de catión, por lo que m = 0. También se ha definido el parámetro l que representa la fracción de los Pares de Defectos Donador-Aceptor (PDDA) por "n" unidades de Cu-III-VI2. Como ya se explicó antes [R2], en la formación de los compuestos Cu-III3-VI5 intervienen un (1) PDDA y cinco (5) entidades de Cu-III-VI2, por lo tanto, l = 1/5 = 0.20.
Recopilación y análisis de data cristalográfica.
En la figura 1 se observa la variación de los parámetros de la celda unidad a, c y el volumen V, obtenidos en mis trabajos de investigación y otros reportados en la literatura, en función de los parámetros m y l. Se incluyen los puntos experimentales correspondientes a otros compuestos de Cun-3(In,Ga)n+1(Se,Te)2n.
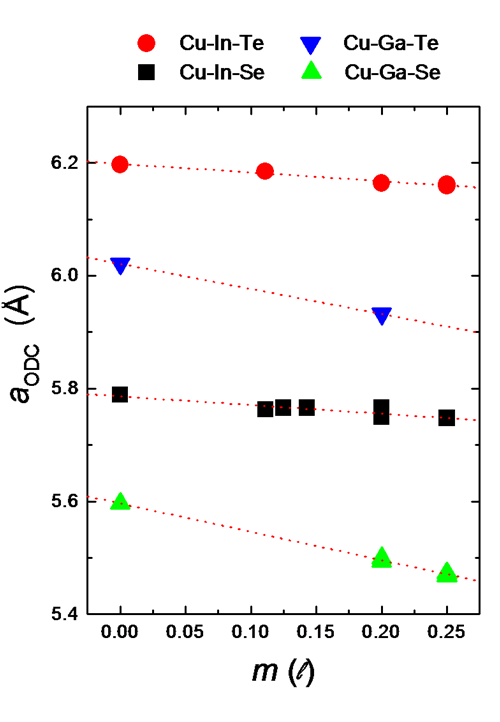 |  | 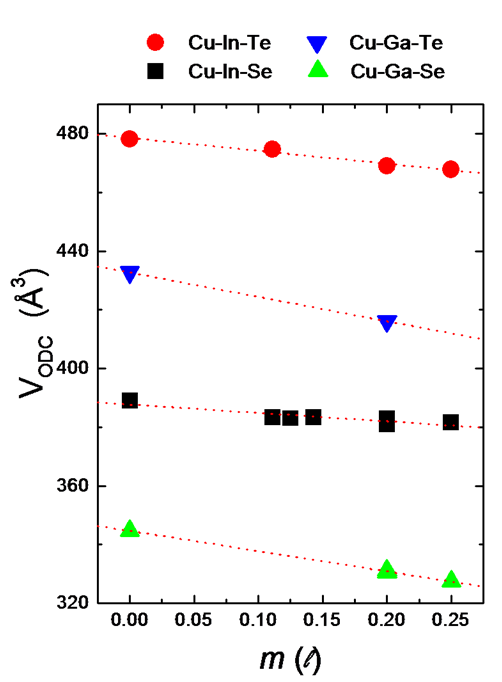 |
Figura 1 del autor @iamphysical: Variación de los parámetros a, c y el volumen V de la celda unidad en función de m y l.
Se puede concluir que el tamaño de la celda unidad de los compuestos con defectos ordenados (CDO) está determinada por los PDDA y como era de esperarse, es de menor volumen en comparación con los compuestos de la familia Cu-III-VI2 debido a la vacancia de cationes.
En este caso no se forma una curva de Arquitas tan complicada, solamente una dependencia lineal como se esperaba!. Este resultado parcial tiene gran importancia, ya que permitiría predecir los parámetros de la celda unidad de otros CDO de 1 ó 2 vacancias que tengan estructura calcopirita, que no hayan sido reportados o que sean difíciles de obtener, como en el caso de los semiconductores que contienen azufre (S) que resulta ser muy explosivo.
En la siguiente tabla se presentan los valores de m, l, el radio efectivo del catión reff, los parámetros de la celda unidad a, c y V, del sistema Cun-3(In,Ga)n+1(Se,Te)2n, y sus correspondientes valores normalizados [R3].

Para estudiar el significado físico de la dependencia lineal de a, c y el volumen V de la celda unidad en función de m y l, se define un radio efectivo de los cationes 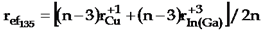 . En esta expresión n = 5 para el caso de los CDO de la familia Cu-III3-VI5. Para los compuestos de la forma CuX-IIIY-VIZ que no se pueden obtener de la fórmula Cun-3 IIIn+1 VI2n que corresponde a los CDO.
. En esta expresión n = 5 para el caso de los CDO de la familia Cu-III3-VI5. Para los compuestos de la forma CuX-IIIY-VIZ que no se pueden obtener de la fórmula Cun-3 IIIn+1 VI2n que corresponde a los CDO.
El radio efectivo de los cationes se calcula mediante la relación:  , donde
, donde 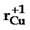 ,
,  y
y 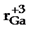 son los radios iónicos [R4] del Cu+1 = 0.60 Å, In+3 = 0.76 Å y Ga+3 = 0.61 Å, respectivamente.
son los radios iónicos [R4] del Cu+1 = 0.60 Å, In+3 = 0.76 Å y Ga+3 = 0.61 Å, respectivamente.
Luego de realizar los cálculos con esta ecuación y los datos aportados, procedí a elaborar la figura 2:

Figura 2 del autor @iamphysical: Variación del radio efectivo de los cationes en función de m y l en los compuestos de las familias 1:1:2 y CDO.
Aportes de esta investigación.
En síntesis, se ha realizado un estudio comparativo de los parámetros de la celda unidad a, c y volumen de los compuestos ternarios calcopiritas de las familias Cu-III-VI2 y Cu-III3-VI5 y se ha determinado que estos parámetros decrecen al incrementarse m y l.
Para explicar el significado físico de este comportamiento, se definieron los radios efectivos de los cationes (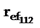 y
y  ) para estas dos familias de compuestos ternarios y se estableció que estos radios disminuyen al incrementarse m y l, reduciéndose la dimensión de la celda unidad en los compuestos con vacancias de cationes.
) para estas dos familias de compuestos ternarios y se estableció que estos radios disminuyen al incrementarse m y l, reduciéndose la dimensión de la celda unidad en los compuestos con vacancias de cationes.
Se ha interpolado la ubicación de otros compuestos con vacancias y caen sobre la tendencia lineal, por lo que podemos formularla como una curva universal para los materiales semiconductores con estructura calcopirita.
Referencias y lecturas recomendadas:
[R1] G. Marín, S. M. Wasim, C. Rincón and L. Essaleh. Materials Letters, 157 (2015), 70.
[R2] S. M. Wasim, C. Rincón, J. M. Delgado, G. Marín, J. Phys. Chem. Solids 66 (2005) 1990.
[R3] C. Rincón, S. M. Wasim, G. Marín, J. M. Delgado, J. Contreras, Appl. Phys. Lett. 83 (2003), 1328.
[R4] R. D. Shanon, Acta Crystallogr. A 32 (1976) 751.
○ Defect physics of the CuInSe2 chalcopyrite semiconductor
○ Propiedades estructurales del AgIn5VI8
○ Defectos en materiales
Saludos cordiales compañero @iamphysical. Dada la complejidad del contenido y el poco manejo que tengo del área de conocimiento, parcialmente capté algunos elementos. Estaré atento y en seguimiento a su blog para conocer y ampliar la información.
Saludos...
Muy acertada tu decisión!
Normalmente eso es lo que yo hago cuando me interesa una temática desconocida, pero interesante, seguir leyendo para adquirir nuevos conocimientos.
Realmente no es mi fuerte este tema pero en la universidad vi una materia tecnología de los materiales y hablaron sobre las propiedades Chalcopirita su nombre científico o como se también se denomina pirita del cobre y sus propiedades gracias a su red cristalina en el sistema tetragonal y su celda es un prisma es un buen conductor
Usted ha recibido un upvote por la comunidad @inteligentzia y su TRAIL de curadores ya que consideramos su post de información útil y de relevancia creativa.
Si quieres saber mas del proyecto aqui te dejamos nuestro post introductorio
Tambien puedes unirte a nuestro canales en el Chat Discord o en nuestro Grupo de Facebook para saber mas del proyecto!
Es un placer leer tus publicaciones @iamphysical. Muy buen artículo sobre la Ciencia de los Materiales que, como sabemos, es muy útil para el avance de la tecnología. Excelente presentación y redacción. Te felicito. Saludos cordiales.
Saludos @iamphysical. Indiscutible sus aportes para la ciencias de los materiales. Mis respetos.
Importante material de consulta para nuestros estudiantes de Ciencias Naturales en la universidad, con miras a aportar a los programas de investigación institucionales. Se agradece este importante aporte estimado @iamphysical
Congratulations @iamphysical! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOP