FUENTES ÓPTICAS –ESTUDIO DE LOS LÁSERES – (PARTE III)
Un saludo mis estimados…!
Nuevamente retomamos el tema de las fuentes ópticas, en el presente texto se concluirá el estudio de esta serie presentando con sumo detalle al “Diodo Laser”, que a diferencia de su hermano el Diodo LED el cual se analizó en la entrega anterior, presenta características un tanto diferentes en cuanto a construcción, rendimiento y efectividad, sin mencionar que el acabado de estos dispositivos resulta considerablemente más costoso.
Antes de desarrollar plenamente el contenido, se ha de mencionar que en la práctica resulta conveniente el disponer del conocimiento apropiado para el diseño e implementación de sistemas ópticos, pues al momento de la elección de la fuente, el decidirse por usar un LED o un Láser conllevaría a optimizar mucho los recursos, bien sean económicos o ingenieriles.
Figura 0 -- Elaboración Propia
Al igual que el LED, un Láser está compuesto por materiales semiconductores, materiales que al aplicarles una corriente específica producirán emisión de luz, la clave radica (y aquí se puede apreciar la primera diferencia entre estas fuentes) en el tipo de emisión producida, en el caso del LED se dijo que la radiación de fotones predominante es la emisión espontanea cuyas propiedades fueron analizadas en la parte I de esta serie, para el caso de un Láser ha de considerarse la emisión estimulada , radiación fotónica del tipo “coherente”. Un láser es un dispositivo sumamente complejo, en primeros términos, para que la radiación estimulada se produzca efectivamente se ha de romper la condición de “equilibrio termodinámico”, a continuación se procede a disertar sobre este proceso:
Se parte por la noción de: “inversión de población de electrones”, la cual es fundamental para que la emisión estimulada sea la radiación predominante. La inversión de población es lograda al polarizar con tensión directa a la unión p-n, en este instante, el material semiconductor presentara ganancia óptica.
Entonces, al incidir una potencia Pe en el material, irá teniendo ganancia conforme se propague, en el caso particular se sabe que la dirección es el eje Z (por conveniencia de coordenadas); la expresión que gobierna esta evolución de potencia a lo largo del material es la siguiente:
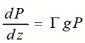
Dada esta ecuación diferencial, se observa que la potencia a lo largo del eje de propagación es equivalente a un escalar proporcional a la potencia en cada punto. Este término “escalar” se compone de un factor de confinamiento Γ y la ganancia del semiconductor, la cual se identifica con la letra g, pues bien, este factor de confinamiento que se ha establecido tiene su interpretación: quizá la totalidad de la potencia no está sufriendo en un 100 por ciento la ganancia del material ya que parte de la potencia de la luz propagada es muy posible que se encuentre en el exterior.
Resolviendo la ecuación diferencial se obtiene la evolución de la potencia con respecto a Z:
La ganancia total se calcula con la diferencia de la tasa de emisión estimulada y la tasa de absorción, para respetar las dimensiones de la ganancia, la cual se expresa en cm^-1 dividimos por la velocidad de grupo de la señal en el medio material, recordar que la tasa de emisión estimulada y de absorción acata unidades de tiempo, s^-1 específicamente:
En efecto, para que la ganancia se produzca, el semiconductor debe contemplar una densidad de electrones inyectados mínima, pues por debajo de este valor el material no será capaz de presentar dicha ganancia. Formalmente la densidad de electrones inyectados se conoce como: Densidad de Transparencia Nt.
La siguiente figura ilustra la dependencia espectral de la ganancia para distintos valores de densidad de electrones inyectados:
Como se puede apreciar, a partir de 1x10^18 electrones por cm^3 se comienza a develar la ganancia y desde este punto en adelante, el espectro va aumentando en anchura.
Para valores de longitudes de onda fijos y tomando en cuenta las ganancias para distintas densidades de electrones se determina que la ganancia varía de forma lineal con “n” (densidad de electrones inyectados), de forma aproximada se establece la siguiente relación:
σg equivale a la pendiente de dicha función y por tanto lleva el nombre de “sección cruzada de ganancia”
La Figura 3 exhibe la dependencia lineal que se comentaba la cual está parametrizada con un recta cuya pendiente es σg, esta recta corta en el valor de n0 que precisamente es el parámetro empleado para aproximar a la ganancia. Los valores típicos para cada caso son los siguientes:
Analizadas las disposiciones iniciales de los láseres se procede a especificar la estructura que estos poseen:
Un láser en concreto, es un oscilador óptico y por tanto está formado por un medio amplificador y una estructura que proporciona realimentación positiva; una forma de proporcionar la realimentación requerida es utilizando una cavidad Fabry-Perot, esta cavidad está formada por dos espejos y un medio activo en su interior, comúnmente es empleado Ti:Sa el cual es un cristal de zafiro dopado con iones de titanio. Si se propaga un campo Ei incidente en dicha estructura, parte del campo será transmitido en el primer espejo y otra parte sufriría reflexión.

Figura N°4 Estructura de un Laser Fabry-Perot – Dra.Ortega (2012)
Para cuantificar los efectos de transmisión y reflexión se emplean los coeficientes de transmitancia t y reflectancia r del espejo en cuestión. El campo se propagara por el medio activo, el factor de propagación se compone de la constante de propagación en el medio, este es un término complejo exponencial el cual se le es adicionado el valor de la ganancia a lo largo de la longitud L:
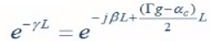
El término negativo de esta expresión no es más que un determinante de posibles absorciones que afecten a la señal dentro de la cavidad. Como ya se ha de notar e^-γL es el factor que resume toda la propagación en un viaje de ida a lo largo de la cavidad. Llegada la señal al segundo espejo parte se transmite con t2 y parte se refleja con r2; esta señal reflejada retornara al primer espejo repitiendo el proceso de forma sucesiva. Todos los campos sumados comprenden el campo resultante a la derecha de la estructura Fabry-Perot (ver Figura N°4).
El campo de salida se calcula sumando todos los campos de la derecha, esta suma es equivalente a la sumatoria de una progresión geométrica la cual estará definida por el campo de entrada y los coeficientes ‘r’ y ‘t’ de ambos espejos:
Construyendo la Cavidad
En cuanto a la configuración de la cavidad fabry perot, se debe “embutir” una estructura de tipo sándwich o heteroestructura de la unión p-n entre dos espejos formados por el propio corte de dicha heteroestructura, al aplicarse un corte recto y limpio en ambos extremos del material semiconductor, provocará la aparición del coeficiente de reflexión de Fresnel , lo que conlleva al cálculo de la reflexión en ambos cortes a partir del índice de refracción del medio exterior y el índice de refracción del material.
Convencionalmente, el índice de refracción de un material semiconductor es de 3,5, para el caso del medio exterior que casi siempre es aire el índice esta tabulado a 1, por tanto, el coeficiente de reflexión en potencia que se obtiene de un corte limpio se aproxima a un 30% de reflexión.
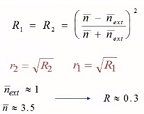
Las medidas de la cavidad están normalizadas con valores específicos , la longitud L tiende a ubicarse entre 100 a 500 µm, la hendidura por donde se proyecta la luz vista desde un corte transversal tiene una altura H que oscila los 0,1 y 0,5µm y la anchura a de ese corte varía entre 5 y 15µm.
Es muy importante señalar que la inyección de corriente se aplicara de arriba hacia abajo como indica la figura 5, esta corriente es la responsable de la inyección de electrones que provocara la inversión de población y con esto la emisión estimulada de fotones.
Continuando con el contenido, se estudian a continuación las características de oscilación de un láser:
Resulta muy interesante y curioso el análisis matemático que fundamenta la oscilación de un láser, en concreto, se debe lograr una señal de salida (de forma forzada) cuya condición será que la señal de entrada en la cavidad sea nula. Partiendo de la expresión de campo resultante en la salida de la cavidad se observa que para lograr dicha condición, el termino Ei deberá ser nulo por lo que el denominador de esta ecuación tendrá que ser 0 y para ello la siguiente función debe cumplirse.
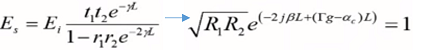
Desarrollando el modulo en ambos terminos de la segunda expresion se obtiene la ecuacion de ganancia:
En pocas palabras esta ecuación indica la ganancia necesaria que debe tener la cavidad para cumplir con la condición de los campos. Esta ganancia umbral es equivalente a las pérdidas α en el resonador más otro termino que representa las perdidas en la señal por los espejos dado un recorrido de ida y vuelta.
Una vez resueltos estos módulos, ahora se procede con las fases de ambos términos, igualando se tiene que:
Esta condición de fase indica que la constante de propagación B por la longitud será un múltiplo entero de π. La constante de propagación se calcula de la siguiente manera:
Donde v es la frecuencia de operación, n’ es el índice de refracción del semiconductor y c la velocidad de la luz.
Sustituyendo en la ecuación de B, tenemos que las frecuencias de oscilación serán múltiplos enteros que satisfacen esta expresión:
Por tanto se tendrá más de una frecuencia que cumple la condición de fase, para determinar la separación entre cada una se tiene que:

Y con esto se ha podido determinar las frecuencias efectivas para un láser del tipo fabry perot, es decir, una señal debe cumplir tanto en modulo como en fase las expresiones que han sido expuestas.
Para dar una explicación más cualitativa de esto, se puede decir que dado el factor de espaciado de frecuencias el cual determina una cantidad de longitudes de ondas aptas para ser propagadas, conlleva a deducir lógicamente que el espectro de emisión de un láser es del tipo multimodo. En la actualidad las fuentes ópticas de Láser cada vez se tornan más “estrechas” para que el efecto de la dispersión sea mínimo en los enlaces ópticos, de igual forma serán deseables estructuras que sean capaces de suprimir la presencia de los efectos producidos por modos de propagación laterales.
Disposiciones finales
En esta sección describirá de forma muy puntual las características de los Láseres en general:
Dada su estructura de confinamiento, los láseres poseen valores de eficiencia modulación cuántica interna bastante elevados lo cual permite que las velocidades de modulación superen a la de los Leds, alcanzando así los 30Gbps. El acople de luz en estas fuentes es mucho más efectivo, en especial en las fibras del tipo monomodo.
Las Características sobresalientes de los láseres son la direccionalidad y la coherencia de fotones emitidos. En cuanto a la direccionalidad, un láser es capaz de emitir un haz de luz recto (en cuanto a dirección) bastante prolongado en distancia sin afrontar tantas perdidas en su potencia; por su parte es te haz será del tipo coherente (recordad el concepto de la emisión estimulada) pues los fotones radiados se transmiten todos en fase uno con respecto a otro.
Con esto damos por finalizado el estudio de las Fuentes Ópticas, un tema muy apasionante y que en lo personal es uno de mis favoritos, espero el contenido les sea de su agrado.
Referencias
Fabry–Pérot Interferometers
Material Audiovisual variado de la Universidad Politécnica de Valencia( UPV) ; MOOC Fundamentos de Comunicaciones Ópticas


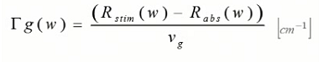

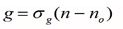

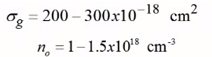



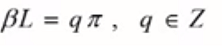

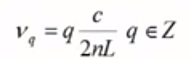
super post, saludos desde Canada
Ah! te invito a conocer nuestro blog es de noticias en Español sobre Bitcoin y criptomonedas, estes al día sobre la nueva economía mundial y si te gusta follow aqui….gracias @criptonoticias
Hola @vjap55 la imagen 1 y 6 tienen derechos de autor