ELECTROMAGNETIC RADIATION: Resolving Power using The Rayleigh Criterion.

Resolving power is the measure of how good an optical system is at clearly distinguishing detail. For example, of two stars close together, or two structures in a living cell. The standard measure of the resolving power of any image-making device is the Rayleigh criterion (due to Lord Rayleigh. Britain 1842-1919).

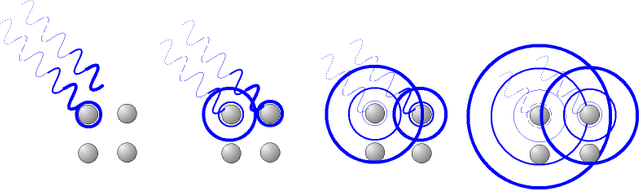
^{Rayleigh diffraction. Christophe Dang Ngoc Chan (cdang) - Own work, CC BY-SA 3.0}

This states that it is possible to separate the images of two point objects if the centre of the central maximum of one image lies on the first dark fringe of the other. This shows that when the criterion is satisfied the central maxima are separated by an angle of θ given by the relationship:

sin θ = 1.22λ/D

In most optical instruments the angles are so small that the criterion is usually written, with θ in radians, as:

θ = 1.22λ/D

AN EXAMPLE USING THE HUBBLE SPACE TELESCOPE

Question: The mirror aperture of the Hubble space telescope has a diameter of 2.40 metres.

• What is its theoretical resolving power in green light of wavelength 5.20 × 10^-7 m?
• At its closest approach, Mars is 7.83 × 10¹⁰ m from Earth. What is the closest possible distance between two small objects on the Martian surface that would allow them to be distinguished as separate by the Hubble telescope?

Answer: Resolving power

θ = 1.22λ/D = 1.22 × 5.20 × 10^-7 ÷ 2.40 giving: θ = 2.6 × 10^-7 radians.

• Let the separation be r metres. The angle subtended by this distance at the telescope must be equal to or greater than θ, so at the limit:

x/7.83 × 10¹⁰ ≥ 2.64 x 10^-7

giving: x ≥ 20 697 m, or 20.7 km

THE DIFFRACTION GRATING AND SPECTRA

The study of the electromagnetic spectra of radiation in and near the visible has produced some of the most important discoveries in science. The element helium is named after the Greek for Sun as it was first identified in the spectrum of sunlight before being discovered as a gas.

Prisms were first used to produce spectra but glass absorbs ultraviolet and some infrared radiation. Prisms are useless for microwave and radio studies.

Modern spectroscopy relies heavily on the principle of the diffraction grating. A diffraction grating is a glass or metal sheet with a large number of very fine parallel lines ruled on it. These lines diffract radiation in such a way that a series of spectra is formed. If the grating lines are close enough together, the spectrum is spread over a very large angle compared to that produced by a prism and much more detail can be observed later on.

Diffraction gratings were used in astronomy to study the spectra of stars and of sunlight from early in the nineteenth century. In 1882, the American Henry Rowland made the first precisely engineered grating, ruling lines with an accuracy and constant separation much better than anyone else had managed.

A typical grating used in school laboratories today might have 5000 lines per centimetre. Transmission gratings are ruled on good optical glass and the radiation passes through the series of slits between grooves ruled on the glass. Cheaper gratings are made by copying these on to a plastic film. Reflection gratings are ruled on good metal mirrors and do not suffer from absorption problems. The mirrors may be curved, to focus the spectra without the need for lenses.

MORE ABOUT DIFFRACTION GRATINGS

We can analyze the principle of the diffraction grating in a similar way to my analysis of the formation of a diffracted image by a narrow slit. The diagram below shows what happens when a plane beam of parallel light (e.g. from a distant point) passes through one slit of a diffraction grating.

Light is diffracted and travels in circular waves from the slit. Suppose the slits are a distance d apart and consider light diffracted at an angle θ. For light with wavelength λ, there is a series of angles θ at which the waves from successive slits reinforce each other by traveling paths that differ by whole numbers of wavelengths λ before they are combined by the lens. This will happen for light diffracted at an angle such that λ = d sin θ. Light with a slightly different wavelength will be diffracted at a slightly different angle. This causes the first order spectrum. Spectra will also occur at other angles for which the path difference for light from adjacent slits is 2λ, 3λ, 4λ, etc. In general, spectra occur at angles given by:

nλ = d sin θ

where n = 2, 3, 4, etc; n = 2 gives the second order spectrum.

THE ENVELOPE OF THE GRATING DIFFRACTION PATTERN

The width b of each slit is also important. The diffracted light forming the spectra must obey the basic diffraction rules for waves passing through a narrow slit: this means that the envelope of the spectra fits into the diffraction pattern produced by a narrow slit of width b.

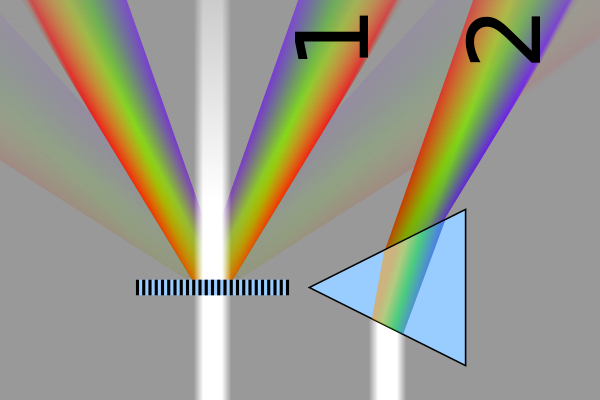
^{Comparison refraction diffraction spectra. Cmglee - Own work, CC BY-SA 3.0}

THE ADVANTAGES OF DIFFRACTION GRATINGS

If d is small, sin θ can be large and so can angle θ. However, if the spectrum is to be detectable, θ must be less than 90°, which means that there is a limit to how widely spread a spectrum can be. The advantage of a diffraction grating, however, is that it can spread a typical spectrum of visible and near visible light over a large enough angle to show its fine detail. Note that although light appears to be ‘destroyed’ in the dark spaces between the orders of the spectrum, the original energy the incoming waves carried has to go somewhere. This means that the visible spectra can be very bright.

In fact for a diffraction grating with many slits, light emitted at angles close to θ will be canceled out and the intensity graph of light of a single wavelength will be very sharp. The sharpness of the peaks means that the grating can distinguish between wavelengths that are very close together. In theory, if a grating has N slits it will produce a line at sin θ for a light of a given wavelength, such that the intensity falls to zero for values which differ from sin θ by sin θ/N. This formula assumes a perfect grating, In practice, however, gratings cannot be ruled to the accuracy that would allow the results to be as good as the formula predicts.

POLARIZATION

Electromagnetic waves are transverse: both the electric and magnetic components oscillate at right angles to the direction of travel. If all the electric oscillations are made to lie in the same plane, the waves are said to be plane-polarized.

The easiest way to polarize a beam of light is to pass it through a sheet of polarized film, manufactured as Polaroid. This contains a large number of small aligned crystals which absorb light whose electric component is aligned along the long axes of the molecules. The emerging beam is thus plane-polarized. This light will not pass through a Polaroid filter whose crystals are aligned perpendicularly to the first.

POLARIZATION BY REFLECTION

When light is partially reflected by a transparent insulator, such as a sheet of glass, both the reflected and refracted light is always partly polarized. When the reflected and refracted beams are at right angles to each other, the reflected light is completely polarized. This occurs at an angle of incidence called the Brewster angle, B, where tan B = n, the refractive index of the reflecting medium.

^{Test for polarized and non-polarized sunglasses. User:Keministi, CC0.}

Polarized light is now a common feature of everyday life. Many people use Polaroid sunglasses, and the liquid crystal displays (LCDs) on watches, calculators, PCs and laptops involve the use of polarized light. Polaroid Sunglasses and filters reduce reflection glare because they absorb the polarized component.

SUMMARY

Having read through all these series of mine on electromagnetic radiation, you should be able to do the following:

• Understand the nature and production of electromagnetic waves.
• Know the properties of the main sections of the electromagnetic spectrum.
• Know what determines the speed of electromagnetic waves and use the formula: c = (ε₀μ₀)^-½
• Understand how Huygens’ principle is used to explain why light travels in straight lines, are reflected and refracted.
• Understand why a change in speed may produce refraction and dispersion of light.
• Understand the principle of superposition for waves.
• Understand the meaning of diffraction and interference and what happens when light passes through a single narrow slit and two narrow slits (Young’s experiment).
• Know and be able to use Young’s two-slit formula: nλ = s sin θ and the formula for fringe separation: Δx = λD/s and know how the experiment may be used to measure the wavelength of light.
• Know the conditions for interference between two wave trains, especially the concept of coherence.
• Understand the meaning of resolution for an optical instrument and the significance of the Rayleigh criterion: sin θ ≈ θ = 1.22λ/D
• Understand how a diffraction grating works, why it is an improvement on prisms for use in spectroscopy and be able to use the grating formula: nλ = d sin θ
• Know the meaning of polarization of light, and how polarized light is produced.

Thanks for reading.

REFERENCES

http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/Raylei.html

https://en.wikipedia.org/wiki/Optical_resolution

https://en.wikipedia.org/wiki/Angular_resolution

http://www.animations.physics.unsw.edu.au/jw/light/diffraction-grating-spectroscopy.html

https://en.wikipedia.org/wiki/Diffraction_grating

https://www.ques10.com/p/37079/what-is-diffraction-grating-what-is-the-advantage-/

https://www.britannica.com/technology/diffraction-grating

https://socratic.org/questions/why-is-diffraction-grating-more-accurate-than-double-slits-to-measure-the-wavele

https://en.wikipedia.org/wiki/Polarization

https://en.wikipedia.org/wiki/Polarization_(waves)

https://www.chegg.com/homework-help/definitions/polarization-by-reflection-2

http://physics.bu.edu/~duffy/sc545_notes08/brewster.html