Combinaciones y el Binomio de Newton
Hola amigos de steemit
Para esta oportunidad les hablare de los números combinatorios, en mi post anterior realizado hace varios días explique como se llega a la expresión de combinación, partiendo del significado de las variaciones y permutación, denotado de la siguiente manera:
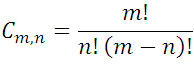
En razón a su origen, suele llamarse números combinatorios y también coeficientes binómicos, porque tienen especial importancia en el desarrollo de las potencias de la forma (a + b)m, para representarlos Euler usaba el símbolo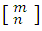 
, pero hoy en día es mas frecuente la notación 
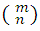, lo que nos deja por definición:
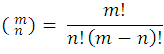
Algunas propiedades fundamentales de los números combinatorios son las siguientes:
El número
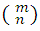, es siempre entero, en efecto como dicho número es igual a Cm,n, y como éste es entero por ser el número de combinaciones de m elementos tomados n a n, también lo es el primero.El número
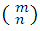es igual al número 
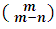. En efecto por definición se tiene que:
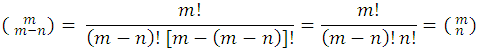
Potencias de un Binomio
Como una aplicación de la teoría combinatoria que acabamos de mencionar, explicare a continuación la fórmula que expresa el desarrollo de la potencia de un binomio, conocida generalmente con el nombre de Fórmula del binomio de Newton.
Potencias sucesivas de (a + b)
Siguiendo la regla ordinaria de la multiplicación, podemos comprobar que:
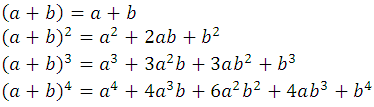
De manera similar se obtendrá para los exponentes 5, 6, etc, pero como este procedimiento se hace cada vez mas laborioso, es conveniente encontrar una ley de formación para estas potencias. En efecto, puede observarse que cada uno de los desarrollos son polinomios homogéneos, completos ordenados y del mismo grado que la potencia del binomio correspondiente, por tanto los desarrollos que se vayan obteniendo de las potencias siguientes serán de la misma naturaleza. Además, como los exponentes de a y b en cualquiera de los desarrollos, el de (a + b)4. por ejemplo, aparecen en el siguiente orden:
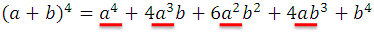
Los exponentes de a marcados con el color rojo: 4, 3, 2, 1, 0, decrecen de 4 a 0, recuerden que podemos asumir que le último exponente de a es 0 por la propiedad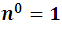 
.
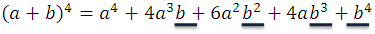
Los exponentes de b marcados con el color azul: 0, 1, 2, 3, 4, crecen de 0 a 4, si los desarrollos siguen este patrón, se puede deducir fácilmente que el próximo de exponente 5, por ejemplo viene de la siguiente forma:
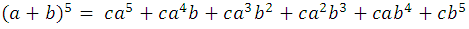
donde c, son los coeficientes del desarrollo, de forma general lo podemos escribir como sigue:
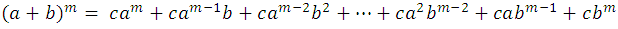
Coeficientes del desarrollo (a+b)m
Se comprende bastante que basta encontrar la formación de los coeficientes, para tener la ley de formación del desarrollo. Fijándonos en los coeficientes de los primeros de los primeros exponentes:
Coeficientes de (a+b) : 1, 1 . Que muy bien pueden escribirse utilizando la notación para la combinaciones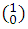 
y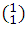 
, es decir, los resultados de las combinaciones corresponde con los coeficientes del desarrollo de exponente 1, análogamente
Coeficientes de (a+b)2 : 1,2,1, que en forma de combinación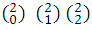 
.
Coeficientes de (a+b)3 : 1,3,3,1 =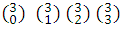 
.
Coefcientes de (a+b)4 : 1,4,6,4,1 =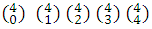 
Así sucesivamente podríamos construir los desarrollos, que de forma general nos queda:
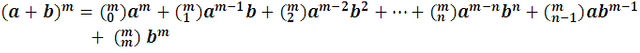
Este último desarrollo suele llamarse Fórmula de Newton o Binomio de Newton, que en su forma compacta :
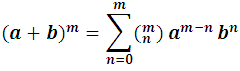
En resumen, podemos decir, que el desarrollo de la potencia emésima del binomio (a+b), siendo m entero y positivo, es un polinomio homogéneo, completo y ordenado de grado m en las letras a y b, cuyos coeficientes son los números combinatorios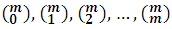 
.
Por ejemplo:
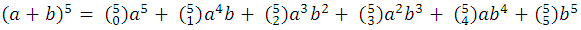
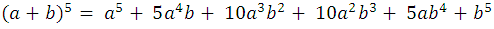
Con esto culmino la explicación del binomio de Newton y su fácil deducción, espero que esta información básica, pero importante sea de ayuda para ustedes mis estimados steemians
bibliográfia:
http://www.cimat.mx/~jortega/MaterialDidactico/EPyE09/Cap2.pdf.
http://www.ub.edu/stat/GrupsInnovacio/Statmedia/demo/Temas/Capitulo1/B0C1m1t13.htm
by @juancmz